Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Арефьев В.П. 1 Михальчук А.А. 1 Филипенко Н.М. 1

---

1 ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет»

Проведен сравнительный статистический анализ качества заочного технического образования на основе результатов входного (ВК) и текущего экзаменационного (ЭКЗ) контроля по высшей математике в рам-ках классической модели организации заочного обучения на примере Томского политехнического уни-верситета в составе 4-х институтов: природных ресурсов, энергетического, физики высоких технологий и неразрушающего контроля. Отмечена очень слабая корреляция и высоко значимое различие между ре-зультатами ВК и ЭКЗ с существенным превышением результатов ЭКЗ над ВК (в среднем на 1,5 балла). На основании однофакторного дисперсионного анализа (рангового критерия Краскела-Уоллиса и пара-метрического F-критерия) сделан вывод о статистически значимой (0,005 < р < 0,05) неоднородности ре-зультатов ВК и сильно значимой (0,0005 < р < 0,005) неоднородности результатов ЭКЗ по совокупности институтов. Для оценки различий между результатами ВК и ЭКЗ по каждому институту применялись параметрический дисперсионный анализ с повторными измерениями и ранговый критерий Вилкоксона для зависимых выборок. В результате различие между ВК и ЭКЗ оценено как статистически значимое (0,005 < р < 0,05) для институтов неразрушающего контроля и физики высоких технологий, а для инсти-тутов энергетического и природных ресурсов как высоко значимое (р < 0,0005). Обсуждаются причины значимых различий между ВК и ЭКЗ и способы их устранения. Результаты проведенного статистического анализа могут быть учтены в рамках проходящей реформы высшего образования.

Статья в формате PDF

304 KB

заочное образование.

входной и текущий контроль математических знаний

Статистический анализ

1. Арефьев В. П. , Михальчук А. А. , Филипенко Н. М. Кластерный анализ результатов оценивания знаний в системе заочного обучения с использованием дистанционных образовательных технологий [Электронный ресурс] // Современные проблемы науки и образования. – 2013 - №. 3. – C. 1-8. – Режим доступа: http://www.science-education.ru/109-9506

2. Арефьев В.П., Михальчук А.А., Болтовский Д.В., Арефьев П.В. Дисперсионный анализ результатов усвоения математических знаний в техническом вузе // Открытое и дистанцион-ное образование. – 2011. - № 1. – С. 43-50.

3. Арефьев В.П., Михальчук А.А., Филипенко Н.М. Дисперсионный анализ качества со-временного заочного технического образования [Электронный ресурс] // Современные про-блемы науки и образования. – 2013. - № 2; URL: http://www.science-education.ru/108-8626 (да-та обращения: 19.03.2013).

4. Боровиков В.П. STATISTICA. Искусство анализа данных на компьютере: Для професси-оналов. – СПб.: Питер, 2003. – 688 с.

5. Гурьянова С.Ю. Качество образования в контексте модернизации высшей школы // Ка-чество. Инновации. Образование. – 2013. - № 1. – С. 3-14.

6. Кон Е.Л., Фрейман В.И., Южаков А.А. Проблема оценки качества обучения в вузах с системой подготовки «бакалавр - магистр» (на примере технических направлений) // Открытое образование. – 2013. - № 1. – С. 23-31.

7. Михальчук А.А., Арефьев В.П., Филипенко Н.М. Сравнительный статистический анализ параметрических и непараметрических методов оценивания знаний в системе заочного обучения [Электронный ресурс] // Современные проблемы науки и образования. – 2013. - № 3; URL: http://www.science-education.ru/109-9553 (дата обращения: 03.09.2013).

8. Образование в ТПУ: итоги 2011/12 учебного года /под ред. А.И. Чучалина, М.А. Соловь-ева. – Томск: Изд-во ТПУ, 2012. – 356 с.

9. Халафян А.А. STATISTICA 6. Статистический анализ данных. Учебник – М: ООО «Би-ном-Пресс», 2008 г. – 512 с.

Главной проблемой современного инженерного образования в условиях модернизации высшей школы является проблема повышения качества образования и оценивания качества обучения в вузах [5, 6] и, в частности, оценка качества образования на этапах приема в вуз и процесса очной формы обучения в вузе [2]. В работах [1, 3, 7] проведен компьютерный статистический сравнительный анализ результатов текущего контроля по математике для студентов-заочников. В Томском политехническом университете (ТПУ) наряду с итоговым семестровым контролем по математике проводится входной контроль (ВК) математических знаний школьной программы на основе аудиторной контрольной работы во время первой сессии с проверкой ее преподавателями. Задание ВК для студентов-заочников содержит 6 задач средней сложности (типа группы В в билетах ЕГЭ). В связи с этим представляет интерес сравнение результатов ВК с результатами итогового семестрового контроля по дифференциальному исчислению (ЭКЗ).

Все числовые результаты ЭКЗ и ВК приведены к единой 5-балльной шкале (делением результата на соответствующий максимальный результат и умножением на пять). Созданная таким образом в MS Excel база данных использовалась далее в пакете Statistica [4, 9] для статистического анализа данных.

Во ВК набора 2012 г. участвовали 130 студентов первого курса ТПУ классической формы заочного высшего образования 4-х институтов [8]: природных ресурсов (ИПР), энергетического (ЭНИН), физики высоких технологий (ИФВТ) и неразрушающего контроля (ИНК).

Статистический анализ начнем с проверки переменных ВК и ЭКЗ на корреляционную зависимость. Матрицы коэффициентов парных корреляций (Пирсона r и Спирмена R) между переменными ВК и ЭКЗ приведены в табл. 1. В круглых скобках указаны соответствующие уровни значимости отличия коэффициентов корреляции от ноля. Согласно табл. 1, корреляцию между ВК и ЭКЗ можно считать в основном незначимой (р > 0,10). Исключение составляют результаты по ИПР: r ≈ 0,26 можно считать слабо значимо (0,05 < р ≈ 0,078 < 0,10), а R ≈ 0,31 статистически значимо (0,005 < р ≈ 0,034 < 0,05), отличными от ноля, хотя весьма далекими от единицы.

Таблица 1. Матрица коэффициентов парных корреляций Пирсона r и ранговых корреляций Спирмена R между переменными ВК и ЭКЗ с соответствующими уровнями значимости (р) отличия от ноля.

Для оценки значимости отличия результатов ВК и ЭКЗ рассмотрим совместное распределение их выборок (рис. 1) по 5-ти балльной равномерной шкале и показывающее наглядно существенные различия в распределениях ВК и ЭКЗ. При этом результаты ВК намного хуже результатов ЭКЗ. Превышение результатов ЭКЗ над ВК можно объяснить тем, что к экзамену студент готовился, а ВК проводился без предупреждения.

Рис. 1. Составная гистограмма результатов ВК и ЭКЗ

Заметим, что сглаживанию различий результатов ЭКЗ и ВК могло бы способствовать придание официального статуса ВК в целях повышения серьезного отношения к нему.

Для корректного сравнения зависимых выборок ВК и ЭКЗ необходимо предварительно проверить выборку поэлементной разности ЭКЗ – ВК на нормальность распределения (рис.2). Отметим существенный разброс значений разности результатов ЭКЗ – ВК, что также подтверждает отсутствие значимой корреляции между ВК и ЭКЗ. Преобладание положительных значений разности результатов ЭКЗ – ВК (≈88%) свидетельствует о существенном превышении результатов ЭКЗ над ВК (в среднем на 1,54 балла). Критерий хи-квадрат показывает сильно значимое отличие (0,0005 < р ≈ 0,0016 < 0,005) распределения переменной ЭКЗ – ВК от нормального. Поэтому для сравнения зависимых выборок ВК и ЭКЗ следует применять, прежде всего, непараметрические критерии. Аналитические ранговые критерии для зависимых выборок (критерий знаков и критерий Вилкоксона) дают очень высокую статистическую значимость различий результатов ВК и ЭКЗ (на уровне значимости р† 0,0005). Параметрический t – критерий для зависимых выборок также подтверждают эту значимость.

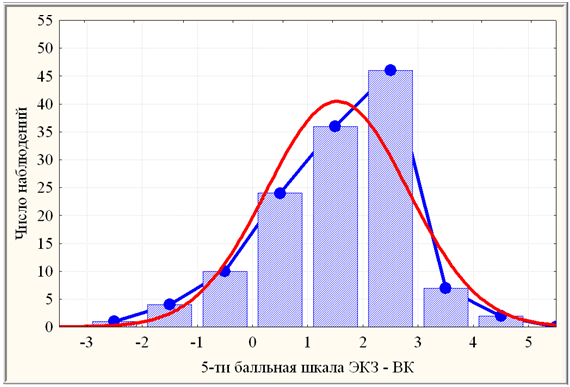
Рис. 2. Гистограмма ЭКЗ – ВК с соответствующей кривой нормального распределения

Выборки ВК и ЭКЗ являются составными. Параметрические (среднее, стандартная ошибка, ±95% границы доверительных интервалов) и непараметрические характеристики выборок (объем n, медиана Ме, минимум Мин, максимум Макс, нижняя квартиль (25% процентиль) и верхняя квартиль (75% процентиль)) результатов ВК и ЭКЗ студентов ТПУ и 4-х институтов приведены в табл. 2.

Таблица 2. Параметрические и непараметрические числовые характеристики выборок результатов ВК и ЭКЗ студентов ТПУ и 4-х институтов

Наблюдаемые распределения (диаграммы размаха) этих выборок результатов ВК и ЭКЗ изображены на рис.3.

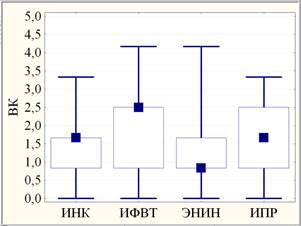
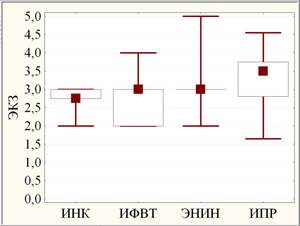
Рис. 3. Диаграммы размаха результатов ВК (слева) и ЭКЗ (справа) по институтам ТПУ 2012 года: медианы (квадраты) с квартилями (прямоугольники) и размахами (усы)

Значения средних баллов результатов ВК и ЭКЗ по институтам с указанием 95 % доверительного интервала приведены на рис. 4.

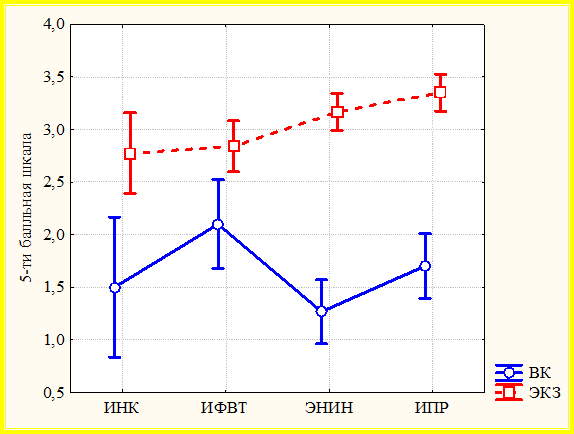
Рис. 4. Линейные графики среднего балла с 95 % доверительным интервалом результатов ВК и ЭКЗ по совокупности институтов

На основании однофакторного дисперсионного анализа оценивается значимость неоднородности результатов ВК и ЭКЗ по совокупности институтов. Ранговый критерий Краскела-Уоллиса приводит к выводу о статистически значимых различиях (на уровне значимости рКУ ≈ 0,025) результатов ВК и сильно значимых различиях (на уровне значимости рКУ ≈ 0,0018) результатов ЭКЗ по совокупности институтов. Заметим, что применение параметрического F-критерия дисперсионного анализа приводит также к выводу о статистически значимой неоднородности (на уровне значимости рF ≈ 0,016) результатов ВК и сильно значимых различиях (на уровне значимости рF ≈ 0,0024) результатов ЭКЗ по совокупности институтов.

Для оценки различий между результатами ВК и ЭКЗ по каждому институту применялся дисперсионный анализ с повторными измерениями (рис. 5). Переменные ВК и ЭКЗ составляют при этом 2-х уровневый фактор повторных измерений (ФПИ). Применение F-критерия однофакторного дисперсионного анализа с повторными измерениями позволило выявить сильно значимые (на уровне р ≈ 0,002) различия между результатами ВК и ЭКЗ по совокупности институтов. Значимость различий между ВК и ЭКЗ по каждому институту оценивалась с помощью параметрического апостериорного критерия наименьших значений разности и рангового критерия Вилкоксона для зависимых выборок. В результате различие между ВК и ЭКЗ оценено как статистически значимое (0,005 < р < 0,05) для ИНК и ИФВТ, а для ЭНИН и ИПР как высоко значимое ( р < 0,00005).

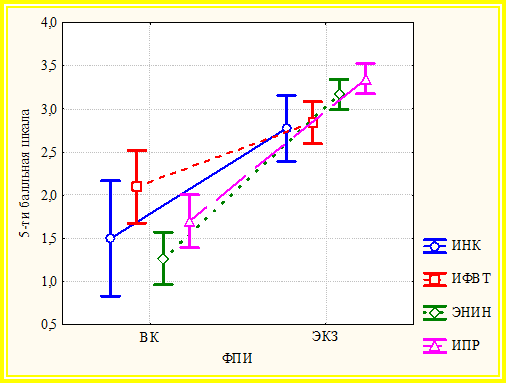
Рис. 5. Линейные графики среднего балла с 95 % доверительным интервалом результатов ВК и ЭКЗ по каждому институту

Заметим, что примененные ранговые и соответствующие параметрические критерии [2, 4, 7] для оценки значимости различий между ВК и ЭКЗ приводят к сопоставимым по значимости результатам.

Выводы

1. Корреляционная зависимость результатов ВК и ЭКЗ является незначимой, за исключением результатов по ИПР, что можно объяснить более высоким конкурсом при наборе студентов в ИПР.

2. Отличия результатов ВК по математике в ТПУ 2012 года от соответствующих результатов ЭКЗ являются высоко значимыми для классической формы заочного образования ТПУ. При этом результаты ВК хуже результатов ЭКЗ в среднем на »1,5 балла, что может быть объяснено снижением уровня требований на итоговом семестровом контроле. Рекомендуется придание официального статуса ВК и внедрение в учебный процесс для студентов-заочников выравнивающего курса по школьной математике.

3. Выборки ВК и ЭКЗ по институтам являются неоднородными: результаты ВК различаются статистически значимо, а результаты ЭКЗ – сильно значимо.

4. Результаты ВК и ЭКЗ по каждому институту различаются значимо: статистически значимо для ИНК и ИФВТ, а для ЭНИН и ИПР высоко значимо.

5. Ранговые и соответствующие параметрические критерии, примененные для оценки значимости различий между ВК и ЭКЗ, приводят к сопоставимым по значимости результатам.

Работа выполнена в рамках государственного задания «Наука» № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России» по контрактам П691.

Рецензенты:

Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.

Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.

Библиографическая ссылка