Введение
Современные системы хранения, передачи и обработки цифровой информации построены с использованием основных положений теории конечных полей. Так, большинство алгоритмов теоретико-числовых преобразований используют процедуры вычисления остатков в конечных полях. Настоятельность данной операции заключается в том, что при выполнении любых типовых арифметических операций в конечных полях результаты вычислений могут выходить за пределы диапазона значений конечного поля, что вызывает необходимость приведения этих результатов в область определений заданного конечного поля. При выполнении различных теоретико-числовых преобразований в системах хранения, передачи и обработки цифровой информации достаточно часто используется операция сложения чисел по модулю. Таким образом, актуальной является задача оценки сложности и быстродействия многоразрядных параллельных сумматоров по модулю с последовательным переносом, которые могут быть использованы при реализации различных теоретико-числовых преобразований в системах хранения, передачи и обработки цифровой информации.
Принципы построения полных многоразрядных сумматоров по модулю состоят в следующем [3].
При сложении двух чисел, представленных в виде двоичных кодов A (a1, ..., an) и
B (b1, ..., bn) образуется сумма С (с1, ..., сn+1). Чтобы найти результат суммирования чисел A и B по модулю M(m1, …mn+1), необходимо найти решение разности С (с1, ..., сn+1) – M(m1, …, mn+1). Если полученное значение отрицательно, то S(s1,…, sn+1)= С (с1, ..., сn+1), если положительное, то S(s1,…, sn+1)= С (с1, ..., сn+1) – M(m1, …, mn+1). Иными словами, принцип построения сумматоров по модулю заключается в реализации следующего способа суммирования двух чисел ![]() и
и ![]() по модулю m. Если (a+b)<m, то выполняется обычное суммирование S=a+b, и эта сумма S является результатом. Если же (S=a+b)>m и по исходному условию сумма S при
по модулю m. Если (a+b)<m, то выполняется обычное суммирование S=a+b, и эта сумма S является результатом. Если же (S=a+b)>m и по исходному условию сумма S при ![]() и
и ![]() не может превышать 2m-2, то из суммы S вычитается значение m и результат является суммой (a+b) mod m [4]. При этом на выходе переноса сумматора, осуществляющего вычитание, появляется сигнал. Данный сигнал является признаком превышения суммой S значения m и используется для выбора результата (a+b) или (a+b)-m. В соответствии с этим полный одноразрядный сумматор по модулю, из которого затем может быть составлен сумматор по модулю для произвольного числа разрядов, должен выполнить суммирование ai и bi разрядов с учетом разряда переноса pi-1 из младших разрядов и полученную сумму Si выдать на выход устройства при отсутствии сигнала переноса модуля со старшего разряда или вычесть из нее разряд модуля mi при наличии такового [2].
не может превышать 2m-2, то из суммы S вычитается значение m и результат является суммой (a+b) mod m [4]. При этом на выходе переноса сумматора, осуществляющего вычитание, появляется сигнал. Данный сигнал является признаком превышения суммой S значения m и используется для выбора результата (a+b) или (a+b)-m. В соответствии с этим полный одноразрядный сумматор по модулю, из которого затем может быть составлен сумматор по модулю для произвольного числа разрядов, должен выполнить суммирование ai и bi разрядов с учетом разряда переноса pi-1 из младших разрядов и полученную сумму Si выдать на выход устройства при отсутствии сигнала переноса модуля со старшего разряда или вычесть из нее разряд модуля mi при наличии такового [2].
Таким образом, одноразрядные сумматоры по модулю должны иметь шесть входов и три выхода, в отличие от обычных сумматоров, которые имеют три входа и два выхода. Дополнительно ко входам разрядов слагаемых ai и bi и входу переноса из предыдущего разряда pi-1 в одноразрядном сумматоре по модулю добавляется вход модуля mi, вход переноса модуля из предыдущего разряда pmi-1 и управляющий вход W. Дополнительно к выходу суммы Si и выходу переноса в следующий разряд pi добавляется выход переноса модуля в следующий разряд pmi.
На рисунке 1 представлена схема одноразрядного параллельного сумматора по модулю с последовательным переносом. На рисунке 2 представлено условное графическое обозначение одноразрядного сумматора по модулю.
Полный одноразрядный сумматор по модулю содержит [1] 7 логических элементов «НЕ», 7 двухвходовых логических элементов «И», 4 четырехвходовых логических элементов «И», 4 трехвходовых логических элементов «И», 2 трехвходовых логических элементов «ИЛИ», 1 четырехвходовый логический элемент «ИЛИ», 1 пятивходовый логический элемент «ИЛИ». На вход 1 подается разряд первого числа суммирования ai, на вход 2 –второго числа суммирования bi. Вход 3 служит входом переноса числа pIni, вход 4 – входом переноса модуля pmIni. На вход 5 подается разряд модуля mi. Вход 6 является управляющим входом W. Выход 7 является выходом переноса pOuti, выход 8 – выходом переноса модуля pmOuti. Выход 9 является информационным выходом Si.
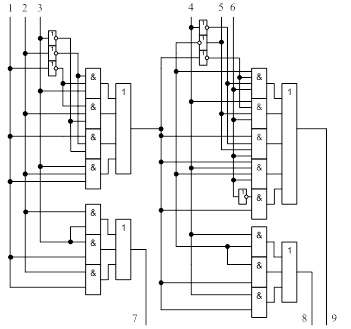
Рисунок 1. Одноразрядный сумматор по модулю
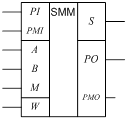
Рисунок 2. Условное графическое обозначение одноразрядного сумматора по модулю
Одноразрядный сумматор по модулю работает следующим образом. Полный одноразрядный сумматор по модулю состоит из логических элементов «НЕ», «И», «ИЛИ», соединенных таким образом, чтобы выполнялись следующие вычисления:
![]() ;
;
![]() ;
;
![]() ;
;
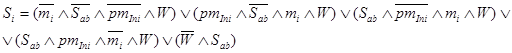 ,
,
где i=0,…,n. Данные выражения составлены в соответствии с таблицей истинности (табл. 1).
Таблица 1. Таблица истинности полного одноразрядного сумматора по модулю (фрагмент)
|
ai |
bi |
pIni |
Sab |
pOuit |
mi |
pmIni |
W |
pmOuti |
Si |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
Для оценки сложности построения сумматора по модулю применим оценку затрат оборудования по Квайну Q, определяемую числом входов всех элементов схемы [5]. Очевидно, что сложность полного одноразрядного сумматора по модулю будет равна Q=56. Оценим быстродействие данного сумматора. Перенос pi и перенос модуля pmi будут формироваться за время равное двум задержкам используемых логических элементов. Время выработки значения суммы Si будет составлять четыре задержки используемых логических элементов. При оценке сложности время и аппаратные затраты на формирование инверсных значений кода входных переменных не учитывалось, так как обычно на шинах данных существуют как прямые, так и инверсные коды.
Предложенный одноразрядный сумматор по модулю является основой для построения многоразрядных параллельных сумматоров по модулю с последовательным переносом. На рисунке 3 представлена схема многоразрядного параллельного сумматора по модулю с последовательным переносом, составленная из полных одноразрядных сумматоров по модулю.
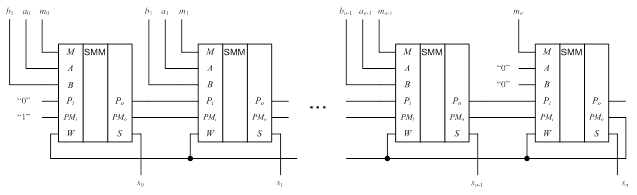
Рисунок 3. Многоразрядный параллельный сумматор по модулю с последовательным переносом
Многоразрядный параллельный сумматор по модулю с последовательным переносом содержит n+1 одноразрядных параллельных сумматоров по модулю, где n количество разрядов чисел суммирования. На вход A n сумматоров подается код числа А, на вход В n сумматоров подается код числа B. На входы A и Bn+1-ого сумматора подаются логические нули. На вход M всех сумматоров подается код числа M. На вход Pi первого сумматора подается логический ноль, на вход PMi первого сумматора – логическая единица. Выход P0j-го сумматора соединен со входом Pi (j+1)-го сумматора, выход PM0j-го сумматора соединен со входом PMi (j+1)-го сумматора, где j=1,…,n. Выход PM0 (n+1)-го сумматора является выходом переноса модуля pmOut устройства, который соединен с управляющим входом W всех n+1 сумматоров. Выходы S всех сумматоров являются информационными выходами устройства, на которые выдается сумма С(с1, ..., сn+1) чисел A(a1, ..., an) и
B(b1, ..., bn) по модулю M(m1, …, mn+1).
Многоразрядный параллельный сумматор по модулю с последовательным переносом работает следующим образом. На информационные входы сумматоров подаются в двоичном виде коды чисел суммирования A(a1, ..., an) и B(b1, ..., bn) и код модуля
M(m1, …, mn+1). Последовательно для каждого разряда каждым одноразрядным параллельным сумматором по модулю формируется перенос числа и перенос модуля. Если сигнал на выходе переноса модуля (n+1)-го одноразрядного параллельного сумматора по модулю равен единице, то из суммы (А+В) вычитается значение модуля, в противном случае два числа A(a1, ..., an) и B (b1, ..., bn) суммируются обычным способом. При этом последовательно поразрядно формируется результат суммирования двух чисел A(a1, ..., an) и B (b1, ..., bn) по модулю M(m1, …, mn+1).
Рассмотрим работу сумматора на примере.
Пусть A=610=1102, B=410=1102, M=910=10012. Воспользовавшись таблицей истинности полного одноразрядного сумматора 1 по модулю (табл.1), найдем промежуточные и конечный результаты суммирования по модулю. Устройство для данного примера будет содержать четыре одноразрядных параллельных сумматора по модулю.
На входы четырех сумматоров подаются коды чисел A=1102, B=1102, M=10012. На выходе первого сумматора P0=0, PM0=0. На выходе второго сумматора P0=0, PM0=1. На выходе третьего сумматора P0=1, PM0=1. На выходе четвертого сумматора PM0=1 эта единица поступает на все входы W всех четырех сумматоров. В результате на выходе первого сумматора S=1, на выходе второго сумматора S=0, на выходе третьего сумматора S=0, на выходе четвертого сумматора S=0. На выходе устройства появляется число 00012=110. Проверим: 6+4=10, 10≡1 mod 9.
Таким образом, оценка сложности и быстродействия многоразрядных параллельных сумматоров по модулю с последовательным переносом показывает, что сложность построения сумматоров составляет 56n, а быстродействие оценивается 4n, где n – количество разрядов сумматора.
Рецензенты:
Тищенко Е.Н., д.э.н., профессор, заведующий кафедрой информационной безопасности Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Ростовский государственный экономический университет (РИНХ)», г. Ростов-на-Дону.
Шуваев А.В., д.э.н., профессор, профессор кафедры прикладной информатики Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Ставропольский государственный аграрный университет», г. Ставрополь.
Библиографическая ссылка
Петренко В.И., Жук А.П., Кузьминов Ю.В., Тебуева Ф.Б. К ВОПРОСУ ОЦЕНКИ СЛОЖНОСТИ ПОСТРОЕНИЯ И БЫСТРОДЕЙСТВИЯ МНОГОРАЗРЯДНЫХ ПАРАЛЛЕЛЬНЫХ СУММАТОРОВ ПО МОДУЛЮ С ПОСЛЕДОВАТЕЛЬНЫМ ПЕРЕНОСОМ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10668 (дата обращения: 16.02.2026).



