В настоящее время состояние российской экономики характеризуется планомерным становлением пути инновационного развития. Реализации государственных мер поддержки и стимулирования инноваций уделяется большое внимание. Утвержден ряд нормативных актов, созданы целевые программы, развиваются инновационные площадки, технопарки и технополисы. Кроме того, очевидно, что в текущей рыночной среде инновационная активность хозяйствующего субъекта является одним из ключевых факторов поддержания конкурентоспособности.
Таким образом, в сложившейся конъюнктуре, вопрос о максимально точной оценке инновационного потенциала предприятия является жизненно важным.
В настоящее время существует масса методик оценки инновационного потенциала, классификацию которых уместно представить в виде схемы, представленной на рисунке 1.
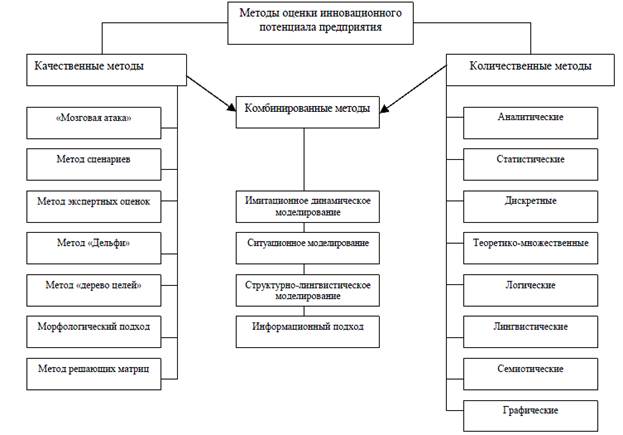
Рис. 1. Классификация методов оценки инновационного потенциала
Процесс выбора методики является одной из наиболее важных и ответственных задач в процессе анализа инновационного потенциала предприятия. Сложность анализа такого рода данных заключается в необходимости учета разного рода неопределенности [2].
На практике при решении задач оценки субъектов хозяйственной и инновационной деятельности наиболее существенны следующие виды неопределенностей:
- неопределенность при формировании оценочной системы;
- неопределенность формирования базы оценки;
- неопределенность оценки по субъективным показателям системы;
- неопределенность при формировании пороговых значений показателей-фильтров;
- неопределенность в определении весов показателей оценки [3].
Помимо факторов неопределенности, специфика оценки инновационного потенциала заключается в том, что она базируется преимущественно на качественных показателях, демонстрирующих состояние предприятия в свете его способности осуществления успешной инновационной деятельности.
Традиционные подходы к оценке инновационного потенциала используют различные методы количественной оценки качественных показателей и их последующей обработки. Однако когда у эксперта отсутствует возможность верифицировать безусловное соответствие качественного параметра определенному количественному значению, такие методы оказываются неэффективными.
Кроме того, инновационный потенциал в итоге также является качественным показателем и его значение, полученное в результате исследования и выраженное численно, не имеет практического значения для руководства предприятия. Эффективным такой результат будет в том случае, если он оценивает возможность организации успешно реализовывать инновационные проекты, создавать и внедрять новшества [1].
Применяемые на текущий момент способы оценки показателей инновационного проекта на основе экспертных оценок либо не учитывают полное разнообразие видов неопределенности, либо устраняют ее из технологии оценки целиком. Однако такие действия приводят к степени неточности оценки, неуместной в современной рыночной среде. Как отмечает А.О Недосекин, «неопределенность – это неустранимое качество рыночной среды, связанное с тем, что на рыночные условия оказывает одновременное воздействие множество факторов различной природы и направленности, не подлежащих совокупной оценке. Но и даже если бы все привходящие рыночные факторы были в модели учтены (что невероятно), сохранилась бы неустранимая неопределенность относительно характера реакций рынка на те или иные воздействия» [4].
Сегодня одним из наиболее перспективных направлений научных исследований в области анализа, прогнозирования и моделирования экономических явлений и процессов является нечеткая логика (fuzzy logic). [6]. В рамках данной теории допустимо сравнение различных моделей, а также возможность количественной оценки понятий «ожидаемый», «высокий», «низкий», «наверняка», «маловероятно» и т.д. Для формализации подобных оценок вводится так называемая лингвистическая переменная, каждому значению которой соответствует нечеткое множество со своей функцией принадлежности фактора данному множеству.
Данная технология не является полностью самостоятельным методом, а применяется в комплексе с существующими способами оценки для анализа и учета неопределенности. Для исследования экономических явлений теория нечетких множеств применяется совместно с методами экспертных оценок и количественными методами на основе аппарата математической статистики.
Характерной особенностью применения теории нечетких множеств является то, что она имеет дело с явлениями, показатели которых не имеют точных границ. Если теория вероятностей связана с экспериментально установленной частотой какого-либо явления, то теория нечетких множеств оперирует возможностью появления события, что является лингвистическим определением, основанным на экспертном мнении, а не фактом математической статистики. Также отличие данных методов заключается в различном происхождении неопределенности. В теории нечетких множеств неопределенность связана с неоднозначностью оценки явления, а в теории вероятностей – со случайностью.
Нечетко-множественное моделирование актуально в тех случаях, когда необходимо получение максимально полных данных при отсутствии точной информации о явлении. Таким образом, данная методика уместна к применению для ситуаций, когда отсутствуют точно установленные факторы, по значениям которых можно сделать безусловный вывод о принадлежности элементов к какой-либо группе.
Базовым понятием нечеткой логики является функция принадлежности, которая представляет собой некоторую субъективную меру соответствия элемента нечеткому множеству. Может принимать значения от нуля, который обозначает абсолютную не принадлежность, до единицы, которая, наоборот, говорит об абсолютной принадлежности элемента нечеткому множеству. Наиболее часто используется линейные, треугольные и трапециевидные виды функции принадлежности [5].
Применяя теорию нечетких множеств для оценки инновационного потенциала предприятия, необходимо создать нечеткую модель. Соответственно, требуется задать множество значений показателей, составляющих инновационный потенциал, и определить на этом множестве нечеткое множество «высокий уровень», что будет демонстрировать готовность предприятия к успешной реализации инновационных проектов. Следовательно, функция принадлежности определит степень принадлежности показателей к нечеткому множеству, что отразит уровень инновационного потенциала.
Предположим, что имеется система показателей, характеризующих уровень инновационного потенциала, состоящая из нескольких групп, из которых сформируются следующие рейтинги:
- финансовый;
- научно-исследовательский;
- производственно-технологический;
- информационный.
Для оценки рейтингов проекта применяется метод экспертных оценок, устанавливая балл и вес каждого показателя по i-й группе. Тогда рейтинг проекта
Yi = ∑bij cij ,
j =1
где i – номер группы показателей инновационного потенциала , ![]() – номер показателя в группе, bij – балльная оценка показателя; сij – весовой коэффициент показателя,
– номер показателя в группе, bij – балльная оценка показателя; сij – весовой коэффициент показателя, ![]() .
.
Построим нечеткую модель для расчета финансового рейтинга предприятия. Для этого введем следующие условные обозначения: Z1 – универсальное множество значений финансового рейтинга предприятия; Y1 – финансовый рейтинг предприятия.
На множестве Z1 нечеткое множество «высокий финансовый рейтинг» ![]() , где
, где ![]() и
и ![]() – функция принадлежности от Y1, принимающая значения от 0 до 1.
– функция принадлежности от Y1, принимающая значения от 0 до 1.
Значение функции принадлежности ![]() для конкретного значения Y1 отражает степень принадлежности финансового рейтинга Y1 к нечеткому множеству А1. Числовое значение
для конкретного значения Y1 отражает степень принадлежности финансового рейтинга Y1 к нечеткому множеству А1. Числовое значение ![]() характеризует возможность высокой оценки финансового потенциала предприятия.
характеризует возможность высокой оценки финансового потенциала предприятия.
Для определения значения ![]() необходимо задать вид функции принадлежности. Предположим, она принимает «треугольную» форму. Зададим на рисунке 2 значение Y1 max , которое определяется из условия максимально возможного финансового рейтинга Y1, исходя из выбранной шкалы.
необходимо задать вид функции принадлежности. Предположим, она принимает «треугольную» форму. Зададим на рисунке 2 значение Y1 max , которое определяется из условия максимально возможного финансового рейтинга Y1, исходя из выбранной шкалы.
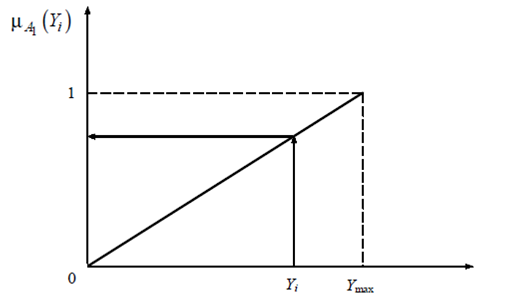
Рис. 2. Определение значения функции принадлежности нечеткого множества
Тогда функция принадлежности:
![]()
Таким образом, определяются функции принадлежности для научно-исследовательского, производственно-технологического и информационного рейтинга предприятия. После получения качественной трактовки составляющих инновационного потенциала целесообразно определить «узкие места» и рекомендации по улучшению соответствующих показателей, а также обозначить наилучшие возможности для успешного внедрения инноваций. Данные рейтинги необходимо трансформировать в итоговый интегральный показатель, демонстрирующий степень принадлежности уровня инновационного потенциала лингвистическому терм-множеству.
![]()
Данный показатель позволяет менеджменту сделать соответствующее заключение о готовности предприятия к успешной реализации инновационных проектов. Необходимо учитывать, что высокий уровень инновационного потенциала означает наличие у предприятия соответствующих возможностей и ресурсов для осуществления инновационной деятельности, но не гарантирует успех конкретного проекта.
Статья опубликована при финансовой поддержке Минобрнауки России в рамках Программы стратегического развития БГТУ им. В. Г. Шухова на 2012–2016 годы (№ 2011-ПР-146).
Рецензенты:
Аркатов А. Я., д.э.н., профессор, БГТУ им. В.Г. Шухова, г. Белгород.
Рудычев А. А., д.э.н., профессор, БГТУ им. В.Г. Шухова, г. Белгород.
Библиографическая ссылка
Гетманцев А.А., Сомина И.В. ТЕОРИЯ НЕЧЕТКИХ МНОЖЕСТВ КАК МАТЕМАТИЧЕСКИЙ АППАРАТ ДЛЯ ОЦЕНКИ ИННОВАЦИОННОГО ПОТЕНЦИАЛА ПРЕДПРИЯТИЯ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10643 (дата обращения: 28.01.2026).



