Введение
В современном мире всё чаще и чаще на производстве вместо людской рабочей силы отдается предпочтение роботизированным и робототехническим системам. Роботы во много раз превосходят человека в монотонной и требующей большого сосредоточения работе. Для продуктивной работы роботизированных систем требуется точное и емкое написание системы управления (СУ). Система управления должна четко отражать в себе поставленную перед роботом задачу и позволять принимать адекватные решения в различных нестандартных ситуациях. Возможны различные принципы построения таких СУ, среди них замкнутые системы c классическим регулятором вход-выход, регулятором состояния, адаптивным регулятором, нечеткая логика, нейронные сети, четкая логика и др. В данной работе предлагается рассмотреть идею построения системы управления движением мобильного робота на основе нечеткой логики (НЛ), которая должна позволить роботизированной платформе с заданной точностью и минимальной погрешностью эффективно выполнять поставленные задачи, несмотря на различные известные и неизвестные возмущения окружающей среды [3].
Разрабатываемая СУ на основе НЛ включает в себе базу нечетких правил для адекватного реагирования на условия окружающей среды, а также набор лингвистических переменных, позволяющих преобразовать реальные числовые параметры системы управления приводами движения робота в словесные переменные нечеткой логики [2]. Функциональная схема системы управления с нечётким регулятором представлена на рисунке 1.
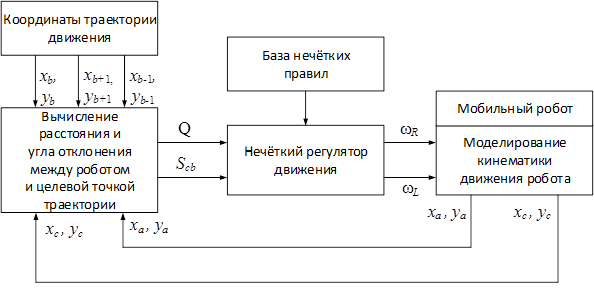
Рисунок 1. Структурная схема процесса моделирования системы управления движением по траектории
На схеме обозначены: xb, yb, xb-1, yb-1, xb+1, yb+1 – координаты текущей, предыдущей и последующей целевых точек заданной траектории; xc, yc и xa, ya – координаты робота в текущий и предыдущий момент времени; Scb – расстояние робота до целевой точки; Q – угол отклонения робота от траектории; ωR и ωL – угловые скорости, задаваемые на приводы движения робота.
Рассмотрим более подробно блоки, входящие в функциональную схему системы управления, а также принципы вычисления и формирования управляющих воздействий на электроприводы колес робота.
Одним из основных блоков, необходимых для организации управления, является блок вычисления расстояния и угла отклонения между роботом и целевой точкой траектории. На основе схемы движения робота от текущей точки к целевой (рис. 2) составлены формулы расчёта расстояний Sac, Sab, необходимые для определения входных величин нечёткого регулятора – расстояния Scb и угла Q.

Рисунок 2. Схема расчёта расстояния и угла отклонения робота между роботом и целевой точкой траектории
Угол отклонения робота от траектории, согласно рисунку 2, вычислим по выражению:
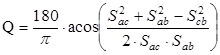 . (1)
. (1)
Необходимые для расчёта угла расстояния можно определить по следующим выражениям:
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() . (4)
. (4)
Согласно формулам 1 – 4, на основе входных данных о координатах заданной траектории и координатах робота, в текущий и предыдущий моменты времени выполняется расчёт расстояний и угла отклонения.
Далее требуется локализовать текущее положение робота по отношению к траектории для формирования лингвистических правил управления приводами колес робота. Для этого предлагается, согласно уравнению прямой по координатам точек траектории и текущим координатам робота, определить знак угла Q по выражению:
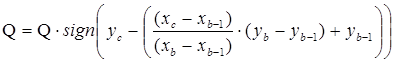 . (5)
. (5)
Последний этап вычислений – формирование движения робота по заданной траектории. Для этого проверяется условие Scb < ∆S, и с заданной точностью осуществляется переключение целевой точки.
Следующим блоком в схеме управления является нечёткий регулятор движения, который, согласно базе нечётких правил (таблица 1), формирует управляющие воздействия на приводы колес робота.
Таблица 1 – База нечётких правил для регулятора движения
|
Угловая Скорость |
Расстояние до целевой точки траектории Scb , м |
||||
|
Близко |
Подальше |
Далеко |
Очень далеко |
||
|
Q, град |
Сильно слева |
Быстрая/ -Быстрая |
Быстрая/ -Быстрая |
Быстрая/ -Быстрая |
Быстрая/ -Быстрая |
|
Средне слева |
Средняя/ -Средняя |
Средняя/ -Средняя |
Средняя/ -Средняя |
Средняя/ -Средняя |
|
|
Слабо слева |
Медленная/ -Медленная |
Медленная/ -Медленная |
Медленная/ -Медленная |
Медленная/ -Медленная |
|
|
Норма |
Медленная/ Медленная |
Средняя/ Средняя |
Быстрая/ Быстрая |
Быстрая/ Быстрая |
|
|
Слабо справа |
-Медленная/ Медленная |
-Медленная/ Медленная |
-Медленная/ Медленная |
-Медленная/ Медленная |
|
|
Средне справа |
-Средняя/ Средняя |
-Средняя/ Средняя |
-Средняя/ Средняя |
-Средняя/ Средняя |
|
|
Сильно справа |
-Быстрая/ Быстрая |
-Быстрая/ Быстрая |
-Быстрая/ Быстрая |
-Быстрая/ Быстрая |
|
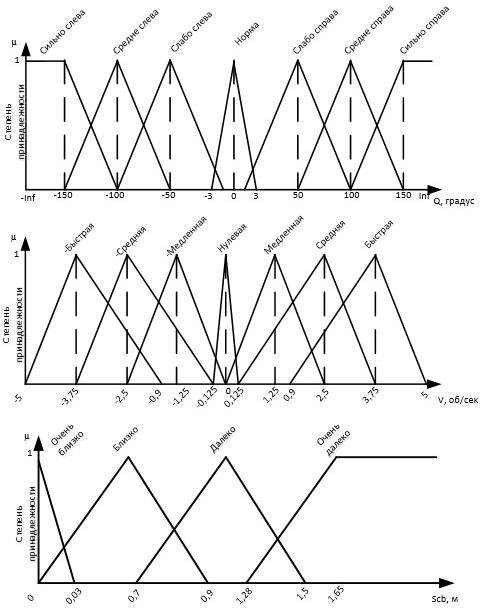
Рисунок 3. Функции принадлежности входных и выходных переменных нечёткого регулятора
Текущие координаты робота определим на основе текущих скоростей робота. Для этого, согласно уравнению кинематики движения, определим линейную скорость движения и угловую скорость поворота робота [5]:
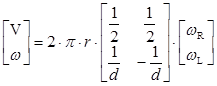 , (6)
, (6)
где V – линейная скорость робота (м/сек), ω – угловая скорость поворота робота (рад/сек), ωR, ωL – угловые скорости вращения левой и правой пары колес (об/сек), r – радиус колеса (м), d – расстояние между левой и правой парой колес или радиус вращения робота (м).
Далее, согласно известным законам движения, определим приращения угла поворота ![]() за время и текущий угол
за время и текущий угол ![]() поворота для ориентации робота в полярной системе координат:
поворота для ориентации робота в полярной системе координат:
![]() =>
=> ![]() (7)
(7)
Вычислив элементарное перемещение робота за время ![]() и зная угол поворота, выполняем переход от полярной системы координат к декартовой:
и зная угол поворота, выполняем переход от полярной системы координат к декартовой:
![]() =>
=>![]() , (8)
, (8)
![]() =>
=>![]() . (9)
. (9)
Реализацию регулятора и системы управления выполним в LabVIEW [4]. Для создания и настройки нечёткого регулятора в меню «Tools» выбираем «Control Design and Simulation» и запускаем «Fuzzy System Designer». В открывшемся диалоговом окне во вкладке «Variables» создаём лингвистические переменные и присваиваем им соответствующие функции принадлежности, согласно рисунку 3. Во вкладке «Rules», согласно таблице 1, задаём базу нечётких правил. Во вкладке «Test System» проводим первичную проверку и тестирование заложенного в регулятор алгоритма управления. В завершении создания базы правил и переменных сохраняем все настройки в файл, который затем будет подключаться на блок диаграмме LabVIEW к блоку нечёткого регулирования.
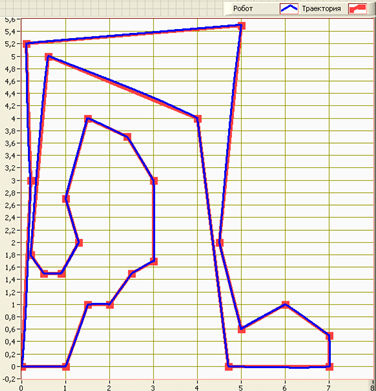
Рисунок 4. Результаты моделирования системы управления движением
На рисунке 4 пунктирной линией и точками обозначена заданная траектория движения, а сплошной линией показана моделируемая траектория движения МИП. Из графика видно, как с довольно высокой точностью нечёткий регулятор отрабатывает движение по заданной траектории. Острые углы при поворотах объясняются особенностью расположения колес мобильного робота, что в совокупности с заданием отрицательных скоростей (ωR, ωL) на приводы позволяет МИП при приближении к целевой точке, согласно базе нечетких правил, выполнять поворот на одном месте, а затем двигаться далее к следующей целевой точке.
Построенная СУ позволяет точно и с минимальными погрешностями следовать роботизированной платформе от одной целевой точки к другой. Таким образом, данную СУ можно использовать в роботизированных платформах, доставляющих какие-либо изделия из одного цеха в другой, а точное следование по целевым точкам позволит платформе с максимальной точностью проходить заданную траекторию передвижения. В итоге предложенные в работе принципы управления движением войдут в единую концепцию построения мобильной интеллектуальной многоцелевой платформы [1].
Рецензенты:
Бочкарёв С.В., д. т. н, доцент кафедры МСА, ПНИПУ, г. Пермь.
Цаплин А.И., д. т. н., зав. кафедрой общей физики, ПНИПУ, г. Пермь.
Библиографическая ссылка
Костыгов А.М., Даденков Д.А., Каверин А.А. НЕЧЁТКАЯ СИСТЕМА УПРАВЛЕНИЯ ДВИЖЕНИЕМ МОБИЛЬНОГО РОБОТА // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10639 (дата обращения: 17.02.2026).



