Введение
Основным фактором, определяющим приведённые температуры на поверхности железнодорожного земляного полотна и примыкающей местности, является температура атмосферного воздуха и условия его теплообмена с поверхностью, зависящие от ветрового режима, солнечной радиации, испарения и т.д.
Численное моделирование процессов промерзания и оттаивания проводилось по теплофизической модели Termoground, позволяющей анализировать процессы промерзания, морозного пучения и оттаивания по установившимся температурным и влажностным полям. Теплофизическая модель грунта Termoground реализована в программном комплексе FEM models.
Расчёт по программе предполагает, что исследуемая область вместе с сооружением разбивается на конечные элементы с одинаковой температурой и характеристиками грунта.
Решение задачи численного моделирования процессов промерзания, морозного пучения и оттаивания в программном комплексе FEM models проводится в два этапа. Первоначально решается теплотехническая задача, в результате которой определяются температурные и влажностные поля на каждый период времени. Вторым этапом решается задача определения напряженно-деформационного состояния грунтов основания в процессе морозного пучения и оттаивания.
Начальным условием является температура грунта, заданная по глубине, граничным условием является температура на поверхности грунта, различная по времени. На верхней границе действует переменный во времени тепловой поток, задаваемый приведёнными температурами воздуха и коэффициентами теплоотдачи. В расчетной модели задаются начальные и граничные условия, далее решается теплотехническая задача, в результате которой определяются температурные и влажностные поля на каждый период времени.
Общее уравнение, описывающее процесс промерзания-оттаивания для нестационарного теплового режима в трехмерном грунтовом пространстве можно представить в виде следующего выражения:
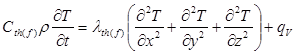
где 
- удельная теплоемкость грунтов (мерзлого или талого); r - плотность грунта;
Т - температура; t - время; 
- теплопроводность грунтов (мерзлого или талого); x, y, z - координаты; qv - мощность внутренних источников тепла.
Основным фактором, определяющим приведённые температуры на поверхности элементов земляного полотна и примыкающей местности, является температура атмосферного воздуха и условия его теплообмена с поверхностью, зависящие от ветрового режима, солнечной радиации, испарения и т.д.
Расчётная величина приведённой среднемесячной температуры воздуха принималась согласно формуле:
,
где 
– среднемесячная температура воздуха, °С; 
и 
– поправки к среднемесячным температурам воздуха за счёт солнечной радиации и испарения, °С.
Расчёт поправки к температуре воздуха за счёт поступления солнечной радиации Dtr установлен по зависимости:
D
,
где 
– коэффициент теплообмена на поверхности грунта, ккал/м2´ч´°С, вычисляемый по эмпирической зависимости:
,
где V – скорость ветра, м/с;
R – среднемесячные суммы радиационного баланса для рассматриваемого элемента поверхности, ккал/см2´мес.
Для горизонтальных поверхностей среднемесячные суммы радиационного баланса определены по формуле:
,
где Qo – среднемесячные суммы суммарной солнечной радиации, поступающей на горизонтальную площадку, ккал/см2´мес.; k – эмпирический коэффициент, зависящий от отражательной способности поверхности (альбедо).
Для наклонных поверхностей (откосы земляного полотна) среднемесячные суммы радиационного баланса определены по формуле:
, ккал/см2´мес.,
где Io и Do – среднемесячные суммы прямой и рассеянной радиации, поступающей на горизонтальную площадку, ккал/см2´мес., их значения взяты из климатологических справочников по ст. Сковородино; mb – безразмерный коэффициент, учитывающий влияние угла наклона поверхности к горизонту и её ориентации в пространстве на поступление прямой солнечной радиации; Pb – коэффициент, учитывающий влияние угла наклона поверхности к горизонту на поступление рассеянной солнечной радиации, определяемый по формуле:
,
где b – угол наклона поверхности к горизонту, град.
Численное моделирование процесса промерзания и оттаивания железнодорожной насыпи
Представленная к расчету насыпь высотой 2,0-4,0 м находится в климатических и мерзлотно-грунтовых условиях Байкало-Амурской магистрали России. Температура воздуха определялась по данным метеостанции станции Сковородино. При этом на окружающей территории поправки на радиацию и испарение приняты равными (=), а на элементах насыпи из-за её незначительности поправка за счет испарения не учитывалась. Теплофизические характеристики грунтов тела и основания насыпи в талом и мёрзлом состоянии приняты в соответствии со СНиП 2.02.04-88. Расчетная схема поперечного профиля земляного полотна приведена на рис. 1.
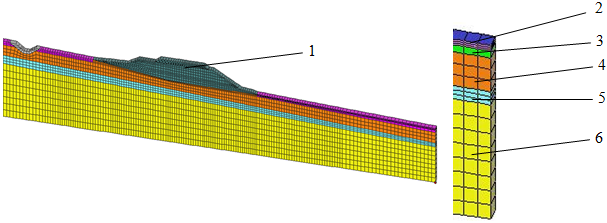
Рис. 1. Расчетная схема поперечного профиля земляного полотна ПК 21055+00
1 - тело насыпи; 2 - почвенно-растительный слой; 3 - торф среднеразложившийся; 4 – супесь; 5 – лед ископаемый; 6 - песок мелкий, льдистый (льдистость 20-40%), при оттаивании водонасыщенный.
Прогнозный расчет выполнен на момент максимального протаивания грунтов – октябрь расчетного года. Расчет производился на 5-й год эксплуатации земляного полотна. Первоначальные температуры грунтов заданы осредненными по данным многолетних температурных наблюдений, выполняемых в термометрических скважинах на ближайшем опытном поперечнике.
Расчеты проводились для 3 вариантов.
Вариант 1. Железнодорожная насыпь высотой 2,0-4,0 м с ездой автотранспорта по основной площадке под второй путь. В основании насыпи на глубине 4,8 м залегает лёд мощностью 1,3 м. Среднегодовая температура воздуха принята по многолетним данным минус 8 °С (СНиП 2.02.04-88).
Температура грунта по глубине принята в соответствии с представленным техническим отчетом инженерно-геологических изысканий.
Результаты расчета показали (рис. 2), что под насыпью оттаивания многолетних грунтов не наблюдается. Однако следует отметить, что при устройстве водоотводной канавы возможно оттаивание льда за счет срезания почвенно-растительного слоя и слоя торфа.
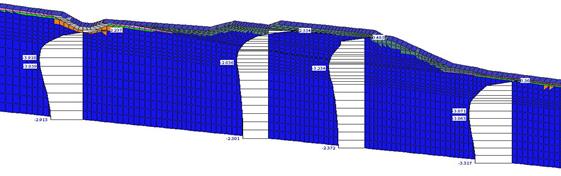
Рис. 2. Эпюры распределения температур на октябрь
Вариант 2. Та же насыпь, но в условиях потепления климата, когда среднегодовая температура, принятая к расчету, повысится на 3 °С и составит минус 5 °С.
Результаты расчёта показали (рис. 3), что под насыпью происходит деградация верхней границы мерзлоты, достигнув толщи льда, что может привести к его оттаиванию и соответственно увеличению деформаций насыпи.
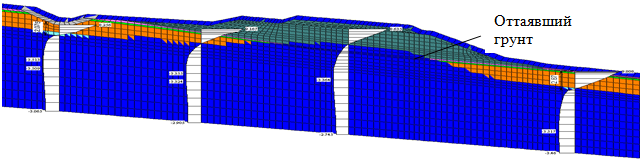
Рис. 3. Эпюры распределения температур на октябрь
Вариант 3. Для прекращения деградации мерзлоты и восстановления температурного режима грунтов в теле и основании насыпи на её откосах применена охлаждающая конструкция. Она представляет собой обсыпку фракционным скальным грунтом откоса и сооружения бермы высотой 1,0 м и шириной 3,0 м со стороны восточного откоса и обсыпки откоса и бермы со стороны западного откоса (рис. 4).
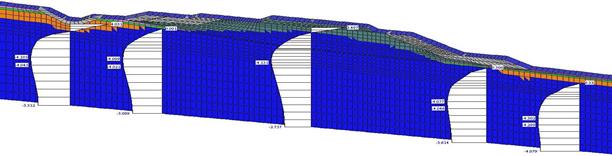
Рис. 4. Эпюры распределения температур на расчетный период времени
Применение скальных набросок, даже в условиях повышения среднегодовой температуры воздуха на 3,0 °С, способствует восстановлению мерзлого состояния грунтов в основании земляного полотна. При этом необходимо обеспечить хорошую работу водоотводных сооружений, исключить застои воды.
Вторым этапом численного моделирования был произведен расчет напряженно-деформированного состояния железнодорожного земляного полотна оттаивающего основания.
Промерзание, морозное пучение и оттаивание влажного грунта являются сложными термодинамическими процессами в промерзающих основаниях. Количественная оценка деформаций грунтов, связанных с морозным пучением и оттаиванием, является одной из сложных задач геомеханики. Основной трудностью решения указанной задачи является необходимость учета изменения состояния грунтов промерзающего и оттаивающего основания и теплофизических характеристик среды в условиях нестационарного состояния. В процессе промерзания и оттаивания одновременно с изменением температурного поля имеет место миграция влаги к фронту промерзания.
При проведении исследований процессов промерзания, морозного пучения и оттаивания целесообразно учитывать зависимость относительной деформации морозного пучения от скорости промерзания грунтов основания, так как процесс морозного пучения в значительной степени обусловлен миграционным подсосом влаги от уровня подземных вод к фронту промерзания.
Основной вклад в деформации морозного пучения вносит переход воды в лед. Кроме того, в тонкодисперсных грунтах промерзание сопровождается миграцией влаги в зоне фазоперехода в спектре отрицательных температур. В итоге происходят подсос воды к фронту промерзания и существенное увеличение объема мерзлого грунта, которое в стесненных условиях вызывает силы морозного пучения, достигающие максимальной величины в направлении промерзания.
Средняя влажность грунта в пределах слоя миграции в зависимости от количества миграционной влаги в зоне определяется по формуле
,
где Qwf – количество миграционной влаги; γd – удельный вес сухого грунта.
Масса миграционной влаги Qwf определяется по формуле
,
где qwf - величина интенсивности миграционного потока влаги; А - площадь сечения миграционного потока; t – время действия миграционного потока.
При анализе существующих зависимостей приращения влажности от скорости промерзания в различных грунтах С.А. Кудрявцевым были подобраны аппроксимирующие функции разных типов грунтов на основе исследований Фельдмана Г.М. и Чистотинова Л.В. Средние значения аппроксимирующих функций зависимости приращения влажности от скорости промерзания на границе фронта промерзания для различных грунтов описываются общим уравнением следующего вида
,
где V – скорость промерзания грунта, b, c – эмпирические коэффициенты.
Параметры прочности грунта задавались на основе параболического уравнения зависимости сопротивления сдвигу от влажности [2]:
,
где Сu – удельное сцепление грунта; w – влажность грунта.
Решалась задача для 2 возможных вариантов напряженно-деформированного состояния:
1. При оттаивании с максимальным обводнением (расчетный уровень воды 1%).
2. При оттаивании без обводнения.
Результаты численного моделирования по 1 и 2 варианту представлены на рис. 5.
а)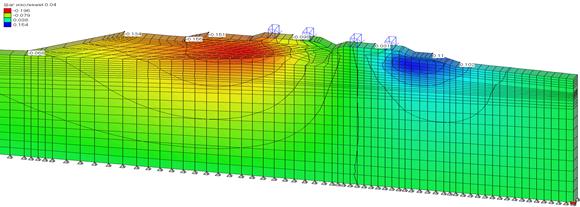
б)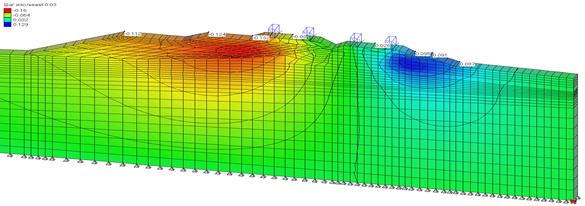
Рис. 5. Изолинии горизонтальных перемещений при оттаивании без подтопления (а) и с возможным подтоплением (б), м
Выводы
1. Результаты численного моделирования показали, что при сооружении охлаждающих скальных набросок на обоих откосах насыпи толщиной не менее 1 м из фракционного камня диаметром 0,2-0,5 м с содержанием не менее 75% по массе следует ожидать эффективную работу набросок при высоте насыпи не менее 4 метров. Учитывая значительную ширину основной площадки насыпи деградация мерзлоты под всей подошвой насыпи маловероятна, вследствие чего прогнозируется подъем верхней границы мерзлоты лишь под бермами и откосами. Это приведет к формированию более благоприятной вогнутой формы ложа протаивания с мерзлыми «упорами» под откосами земляного полотна, препятствующими пластическому выдавливанию слабых оттаявших грунтов, т.е. к повышению их прочности, и в конечном итоге к уменьшению и стабилизации осадок.
2. В результате численного моделирования напряженно-деформированного состояния системы «вечномерзлое основание – железнодорожное земляное полотно» при оттаивании установлено, что при возможном обводнении и изменении прочностных характеристик грунтов возможны осадки по оси пути до 22 см, при необводненном состоянии до 18 см; горизонтальные перемещения возможны до 10 см, 8 см при обводненном и необводненном состоянии соответственно.
Рецензенты:
Парамонов В.Н., д.т.н., профессор кафедры «Основания и фундаменты» ГОУ ВПО «Петербургский государственный университет путей сообщения», г.Санкт-Петербург.
Чехонин К.А., д.ф.-м.н., профессор, заведующий кафедрой «Информационные технологии и системы» ГОУ ВПО «Дальневосточный государственный университет путей сообщения», г.Хабаровск.
Библиографическая ссылка
Кудрявцев С.А., Кажарский А.В. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ПРОМЕРЗАНИЯ И ОТТАИВАНИЯ ВЕЧНОМЕРЗЛОГО ОСНОВАНИЯ КОНСТРУКЦИЙ ЖЕЛЕЗНОДОРОЖНОГО ЗЕМЛЯНОГО ПОЛОТНА // Современные проблемы науки и образования. – 2013. – № 5. ;URL: https://science-education.ru/ru/article/view?id=10558 (дата обращения: 18.04.2024).