Введение
Разработка россыпных месторождений в долинах рек с высоким содержанием глин обычно приводит к значительному загрязнению этих рек взвешенными веществами. Негативные экологические последствия этого выходят далеко за пределы разрабатываемых месторождений.Учитывая, что не менее 50 % одного только золота, добываемого в России, приходится на россыпные месторождения, решение данных экологических проблем становиться особенно актуальным. Существенными затруднениями для организации эффективной очистки воды являются, с одной стороны, значительные объемы загрязненной воды (например, драга может загрязнять порядка 200 л/сек), а, с другой – большое содержание взвешенных частиц, достигающее 2 г/л и более. В этих условиях традиционные системы отстаивания, промышленно производимые фильтры и системы, реализующие электрофоретические методы очистки, не позволяют в достаточной степени очищать весь объем загрязненной воды при сохранении рентабельности разработки месторождения. Наиболее перспективным методом является фильтрование загрязненной воды через техногенные фильтрационные плотины и поля, создаваемые в процессе разработки месторождений. Примером подобного объекта может служить фильтрационное поле, организованное на месторождении алмазов, разрабатываемое дражным способом в долине реки Б. Колчим Красновишерского района Пермской области и описанное в работах [1, 2, 4]. Схема работы такого поля приведена на рис. 1 в работе [5]. Моделированию функционирования подобных объектов посвящена данная работа.
Метод исследования
Исследование свойств техногенных фильтрационных плотин и полей было проведено методом имитационного моделирования.Для проведения моделирования была использована специально разработанная программа «PRIMF.ехе», реализующая модель описанную ниже.
Постулаты и границы применимости имитационной модели:
- принимается следующая структура фильтрационной плотины: в горизонтальных и вертикальных плоскостях, расположенных поперек направления фильтрации плотинаоднородная, распределение размерных фракций кварцевого песка вдоль направления фильтрации подчиняется линейным зависимостям;
- модель не применима для неоднородных плотин, у которых содержание крупных фракций подчиняется возрастающим линейным зависимостям, а для более мелких фракций – убывающим линейным зависимостям;
- модель применима для однородных плотин;
- суммарная доля в фильтрационной плотине кварцевого песка фракций: 2,0–0,5 мм, 0,5–0,25 мм и 0,25–0,1 мм, не менее 10 %;
- доля глинистых частиц в фильтрационной плотине незначительна.
Исходные данные в модели:
- разность высот уровней напорной и отводящей траншеи, (Δh),
- длина (L), ширина (W), толщина (D)фильтрационной плотины,
- линейные зависимости долей в фильтрационной плотине кварцевого песка различных фракций, (xi), задаваемые как xi(0) и xi(L) значения долей фракций в начале и конце плотины, соответственно,
- d1 – больший диаметр частиц самой мелкой фракции песка, т.е. самая мелкая фракция песка – это фракция с частицами диаметрами от 0 до d1,
- di-1 и di – меньший и больший диаметры частиц i-фракции песка (применяется для всех фракций, кроме самой мелкой),
- коэффициент пористости фильтрационной плотины, (КП),
- коэффициент эффективности очистки фильтрационной плотины для взвешенных частиц заданного гранулометрического состава, (КЭО).
Моделируемые величины:
- степень очистки (%), т.е. доля отфильтрованных примесей по отношению к исходному количеству примесей, выраженная в процентах, (СЧ);
- скорость фильтрации, м3/ч.
Метод расчета степени очистки
Степень очистки фильтрационной плотины не может быть больше 100 % и пропорциональна времени фильтрации, поэтому рассчитывается следующим образом:
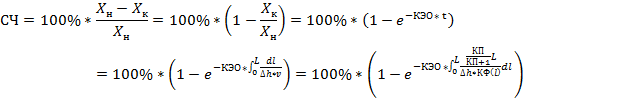
где![]() – объемная доля примесей в исходной воде,
– объемная доля примесей в исходной воде,
![]() – объемная доля примесей в очищенной воде,
– объемная доля примесей в очищенной воде,
![]() – время фильтрации всего объема фильтрационной плотины,
– время фильтрации всего объема фильтрационной плотины,
v – линейная скорость фильтрации,
КФ(l) – коэффициент фильтрации фильтрационной плотины на расстоянии l от начала плотины.
Расчет коэффициента фильтрации плотины на расстоянии l от ее начала проводим аналогично формуле Козени [3], но при этом с целью уточнения этой формулы коэффициент пропорциональности перед квадратом эффективного диаметра частиц песка фильтрационной плотины определяется по экспериментальным данным из регрессионного анализа:
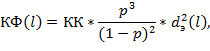
где КК – коэффициент пропорциональности,
p – пористость, определяемая через коэффициент пористости как ![]() ,
,
dэ (l) – эффективный диаметр частиц песка фильтрационной плотины на расстоянии l от начала плотины, которые, в свою очередь, рассчитываются следующим образом:
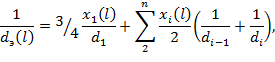
xi(l) – доля i-фракции на расстоянии l от начала плотины в свою очередь, задаваемая линейной зависимостью xi(l) = Ai*l + Bi. В исходных данных заданы доли фракций в начале и конце плотины:xi(0) = Bi, xi(L) = Ai*L + Bi.Следовательно:
Bi = xi(0), ![]()
![]()
Метод расчета скорости фильтрации
Скорость фильтрации определяем следующим образом:
Q = V/t,
где Q – скорость фильтрации, м3/ч,
V – объем воды, заполняющей всю фильтрационную плотину во время фильтрования, м3 ,
t – время фильтрации объема V, т.е. время за которое вода проходит через всю фильтрационную плотину, ч.
Объем воды, заполняющей всю фильтрационную плотину во время фильтрования рассчитываем так:
V = Vфп * p = L * W * D * p,
Vфп – это объем всейфильтрационной плотины, определяемый какVфп = L * W * D,
Следовательно, объем воды, заполняющей всю фильтрационную плотину равен:
![]()
Время фильтрации всего объема фильтрационной плотины рассчитываем так:
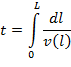
где v (l) – линейная скорость фильтрации на расстоянии l от начала плотины, рассчитываемая так:
![]()
То есть,
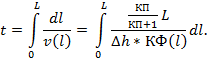
Таким образом, скорость фильтрации определяем так:
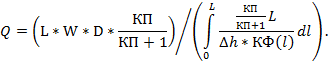
При условии равномерности пористости плотины, т.е. при условии КП = const, получим:
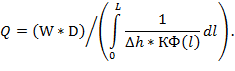
Результаты и обсуждение
Исходные данные для имитационного моделирования
Моделирование было проведено со следующими исходными данными:
А) однородная фильтрационная плотина:
- разность высот уровней напорной и отводящей траншеи, Δh− 1,247 м,
- длина, ширина и толщина фильтрационной плотины − 29 м, 310 м, 5,15 м, соответственно,
- коэффициент пористости фильтрационной плотины − 1,32,
- коэффициент эффективности очистки фильтрационной плотины для взвешенных частиц заданного гранулометрического состава – 3,986,
- линейные зависимости долей в фильтрационной плотины кварцевого песка различных фракций, (xi), заданные как xi(0) и xi(L) значения долей фракций в начале и конце плотины, соответственно, приведены в табл. 1.
Табл. 1. Гранулометрический состав песка однородной фильтрационной плотины
|
Фракции, мм |
+10,0 |
-10,0 +5,0 |
-5,0 +2,0 |
-2,0 +1,0 |
-1,0 +0,5 |
-0,5 +0,25 |
-0,25 +0,1 |
-0,1 +0,05 |
-0,05 +0,005 |
-0,005 |
|
Доля фракции во всей плотине в % |
2,5 |
9,0 |
13,25 |
13,05 |
18,55 |
25,3 |
16,35 |
0,2 |
1,0 |
0,8 |
Б) неоднородная фильтрационная плотина (по распределению фракций песка):
- все исходные данные, кроме гранулометрического состава плотины (см. табл. 2), такие же, как для плотины (А).
В) неоднородная фильтрационная плотина, с большей разностью высот уровней воды, в напорной и отводящих траншеях:
- все исходные данные, кромеΔh, такие же как для плотины (Б),
- Δh=1,31335 м.
Табл. 2. Гранулометрический состав песка неоднородной фильтрационной плотины
|
Фракции, мм |
+10,0 |
-10,0 +5,0 |
-5,0 +2,0 |
-2,0 +1,0 |
-1,0 +0,5 |
-0,5 +0,25 |
-0,25 +0,1 |
-0,1 +0,05 |
-0,05 +0,005 |
-0,005 |
|
Доля фракции в начале плотины в % |
4,3 |
16,0 |
20,8 |
15,8 |
17,1 |
17,2 |
7,7 |
0,1 |
0,6 |
0,4 |
|
Доля фракции в конце плотины в % |
0,7 |
2,0 |
5,7 |
10,3 |
20,0 |
33,4 |
25,0 |
0,3 |
1,4 |
1,2 |
Г) неоднородная фильтрационная плотина с уменьшающимся коэффициентом пористости:
- все исходные данные, кроме приведенных ниже, такие же, как для плотины (Б),
- коэффициент пористости фильтрационной плотины является линейной функцией длины плотины: в начале плотины КП = 1,42, в конце плотины КП = 1,22.
Д) неоднородная фильтрационная плотина с увеличивающимся коэффициентом пористости:
- все исходные данные, кроме приведенных ниже, такие же, как для плотины (Б),
- коэффициент пористости фильтрационной плотины является линейной функцией длины плотины: в начале плотины КП = 1,22, в конце плотины, КП = 1,42,
Е) неоднородная фильтрационная плотина с уменьшенным коэффициентом пористости:
- все исходные данные, кроме приведенных ниже, такие же, как для плотины (Б),
- коэффициент пористости фильтрационной плотины, КП = const =1,22.
Ж) неоднородная фильтрационная плотина с увеличенным коэффициентом пористости:
- все исходные данные, кроме приведенных ниже, такие же, как для плотины (Б),
- коэффициент пористости фильтрационной плотины, КП = const =1,42.
З) неоднородная фильтрационная плотина с большим содержанием мелких фракций по сравнению с плотиной (Б):
- все исходные данные, кроме гранулометрического состава плотины (см. табл. 3), такие же, как для плотины (Б).
Табл. 3. Гранулометрический состав песка неоднородной фильтрационной плотины с большим содержанием мелких фракций по сравнению с плотиной (Б)
|
Фракции, мм |
+10,0 |
-10,0 +5,0 |
-5,0 +2,0 |
-2,0 +1,0 |
-1,0 +0,5 |
-0,5 +0,25 |
-0,25 +0,1 |
-0,1 +0,05 |
-0,05 +0,005 |
-0,005 |
|
Доля фракции в начале плотины в % |
3,3 |
15 |
19,8 |
14,8 |
17,1 |
17,2 |
8,7 |
1,1 |
1,6 |
1,4 |
|
Доля фракции в конце плотины в % |
0 |
0,7 |
4,7 |
9,3 |
20 |
33,4 |
26 |
1,3 |
2,4 |
2,2 |
И) неоднородная фильтрационная плотина с большим содержанием крупных фракций по сравнению с плотиной (Б):
- все исходные данные, кроме гранулометрического состава плотины (см. табл. 4), такие же, как для плотины (Б).
Табл. 4. Гранулометрический состав песка неоднородной фильтрационной плотины с большим содержанием крупных фракций по сравнению с плотиной (Б)
|
Фракции, мм |
+10,0 |
-10,0 +5,0 |
-5,0 +2,0 |
-2,0 +1,0 |
-1,0 +0,5 |
-0,5 +0,25 |
-0,25 +0,1 |
-0,1 +0,05 |
-0,05 +0,005 |
-0,005 |
|
Доля фракции в начале плотины в % |
5,3 |
17 |
21,8 |
16,8 |
17,1 |
17,2 |
4,8 |
0 |
0 |
0 |
|
Доля фракции в конце плотины в % |
1,7 |
3 |
6,7 |
11,3 |
20 |
33,4 |
23,3 |
0 |
0,4 |
0,2 |
Результат моделирования
В качестве отправной точки для объяснения результатов моделирования работы фильтрационных плотин рассмотрим однородную фильтрационную плотину (А) с таким же суммарным содержанием фракций, как у большинства неоднородных плотин. На рис. 1 представлены результаты моделирования: коэффициент фильтрации постоянен и равен 407,825 м/сутки, скорость фильтрации составила 1166,54 м3/ч, степень очистки – 97,65 %. Несмотря на, казалось бы, оптимистичные результаты, на практике такая плотина будет неравномерно «забиваться» отфильтрованными частицами, преимущественно в начале плотины, и через некоторое время плотину будет некорректно рассматривать как однородную, а корректно будет представить ее как неоднородную, у которой вдоль направления фильтрации содержание крупных фракций возрастает, а мелких – убывает. В начале такой плотины вода будет фильтроваться с небольшой линейной скоростью, плотина при этом будет «пропитана» водой практически на всю толщину. Однако потом линейная скорость фильтрации будет резко возрастать, при условии постоянства той же объемной скорости, т.е. плотина будет «пропитана» водой только на часть толщины, пропорциональной отношению линейной скорости в данной точке к линейной скорости в начальной точке плотины. Иными словами, время прохождения порции воды через всю плотину будет уменьшаться и таким образом степень очистки будет меньше, чем должна быть для однородной плотине при полученной объемной скорости фильтрации.
Описанный выше недостаток, когда плотина неравномерно «забивается» отфильтрованными частицами, преимущественно сначала, можно существенно нивелировать на длительное время работы плотины, если плотина будет организована как неоднородная, у которой вдоль направления фильтрации содержание крупных фракций убывает, а мелких – возрастает.
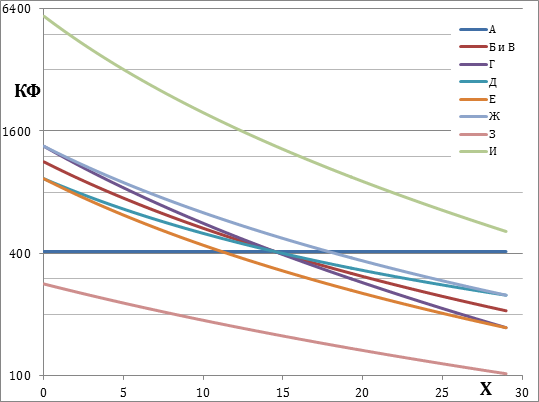
Рис. 1. Логарифмические зависимости коэффициентов фильтрации КФ (м/сутки) промоделированных плотин как функции расстояния (м) от начала плотины КФ = f (l)
На рис. 1. представлены результаты моделирования для такой плотины (Б), причем суммарное содержание фракций во всей плотине такое же, как у плотины (А). Как видно из графика, коэффициент фильтрации обратно пропорционально уменьшается от ~ 1125 до ~ 210 м/сутки. Скорость фильтрации составила 1107,61 м3/ч, степень очистки – 98,07 %. Т.е. для такой плотины наблюдается уменьшение скорости фильтрации на ~5,3 % с одновременным увеличением степени очистки на 0,42 %. Если разность высот уровней воды в подводящей и отводящей траншеях увеличить с 1,247 м до 1,31335 м (плотина (В), т.е. на ~5,3%, то скорость фильтрации и степень очистки станут такими же, как у однородной плотины, т.е. 1166,54 м3/ч и 97,65 % (см. рис. 1). При этом зависимость коэффициента фильтрации от расстояния от начала плотины будет такой же, как у неоднородной плотины (Б).
Для цели дальнейшего развития понимания поведения плотин рассмотрим неоднородные плотины, аналогичные (Б), но 1) с линейноуменьшающимся и увеличивающимся коэффициентом пористости (КП) плотин, (Г) и (Д), соответственно, 2) с постоянным КП меньшим и большим по сравнению с плотиной (Б). Зависимости коэффициентов пористости плотин (Г) и (Д) подобраны таким образом, чтобы средние значения КП этих плотин равны КП плотины (Б), а минимальные и максимальные КП плотин (Г) и (Д) равны между собой и равны постоянным КП плотин (Е) и (Ж). Результаты моделирования представлены на рис. 1 и в табл. 5. Для всех этих плотин характерно качественно одинаковое обратно пропорциональное уменьшение коэффициента фильтрации с увеличением расстояния от начала плотин, но сами значения величины КФ явно прямо пропорционально зависят от коэффициента пористости. Скорость фильтрации, в свою очередь, прямо пропорционально зависят от коэффициента фильтрации, причем, увеличение значения меньшего КФ плотины (т.е. КФ конечного участка плотины в направлении фильтрации) в заметно большей степени увеличивает скорость фильтрации по сравнению со значением большего КФ плотины (т.е. КФ начального участка плотины в направлении фильтрации). Самая медленная плотина (Е) (КП = 1,22) КФ от ~ 930 до ~ 250 м/сутки, скорость фильтрации – 913,86 м3/ч. Далее плотина (Г) (КП = 1,42-1,22), у которой больший КФ возрос на 44 %, а скорость фильтрации возросла на 14,8 % по сравнению с (Е). Затем плотина (Д) (КП = 1,22–1,42), у которой меньший КФ возрос на 43 %, а скорость фильтрации возросла на 26 % по сравнению с (Е). Наконец самая быстрая плотина (Ж) (КП = 1,42), у которой меньший КФ возрос на 43 %, больший – на 44 %, а скорость фильтрации возросла на 44,7 % по сравнению с (Е). Степень очистки прямо пропорциональна времени фильтрации и, соответственно, обратно пропорциональна скорости фильтрации, что и наблюдается в результатах моделирования. Степень очисткиэтих плотин варьируется в диапазоне от 96,71 % для самой быстрой (Ж) до 99,02 % для самой медленной (Е).
Табл. 5. Результаты моделирования плотин (Б), (Г), (Д), (Е), (Ж)
|
Плотина |
КП |
КФ, м/сутки |
Скорость фильтрации, м3/ч |
Степень очистки, % |
|
(Б) |
1,32 |
1125-240 |
1107,61 |
98,07 |
|
(Г) |
1,42-1,22 |
1340-175 |
1049,24 |
98,39 |
|
(Д) |
1,22-1,42 |
930-250 |
1151,84 |
97,81 |
|
(Е) |
1,22 |
930-175 |
913,86 |
99,02 |
|
(Ж) |
1,42 |
1340-250 |
1321,91 |
96,71 |
Рассмотрим еще влияние содержания мелких фракций на производительность плотин. Для этого, первое, промоделируем работу плотины (З) при сохранении всех условий, как у плотины (Б), за исключением гранулометрического состава: увеличим на 1 % содержание каждой из четырех мелких фракций (-0,25+0,1 мм; -0,1+0,05 мм; -0,05+0,005 мм; -0,005 мм), содержание каждой из четырех крупных (+10,0 мм; -10,0+5,0 мм; -5,0+2,0 мм; -2,0+1,0 мм), соответственно уменьшим на 1 %, а содержание двух средних (-1,0+0,5 мм; -0,5+0,25 мм) оставим прежним. Второе, промоделируем работу плотины (И) при сохранении всех условий как у плотины (Б) за исключением гранулометрического состава: уменьшим на 1 % содержание каждой из четырех мелких фракций (в случаях когда содержание фракций –0,1+0,05 мм; -0,05+0,005 мм; -0,005 мм плотины (Б) было меньше 1 %, то оно было уменьшено до 0 в плотине (И), а недостающее уменьшение было «перенесено» на фракцию –(0,25+0,1 мм), содержание каждой из четырех крупных (+10,0 мм; -10,0+5,0 мм; -5,0+2,0 мм; -2,0+1,0 мм), соответственно увеличим на 1 %, а содержание двух средних (-1,0+0,5 мм; -0,5+0,25 мм) оставим прежним. Диапазоны значений КФ значительно отличаются от полученных ранее и составляют от ~282 до ~102 м/сутки для плотины (З) с увеличенным содержанием мелких фракций по сравнению с плотиной (Б) и от ~5850 до ~670 м/сутки для плотины (И) с уменьшенным содержанием мелких фракций. Скорости фильтрации составили 445,96 и 3384,41 м3/ч для плотин (З) и (И), соответственно. Степени очистки в свою очередь составили 99,99 % и 72,13% для плотин (З) и (И), соответственно. Скорость фильтрации плотины (З) уменьшилась приблизительно в 2,5 раза, тогда как степень очистки увеличилась на 1,92 % и практически достигла максимального значения, составив 99,99 %. Скорость фильтрации плотины (И) увеличилась приблизительно в 3 раза, тогда как степень очистки уменьшилась на 25,94 % и немного больше четверти исходных взвешенных частиц пройдет через плотину. Работу таких плотин можно будет признать неудовлетворительной: (З) в отношении скорости фильтрации, а (И) – степени очистки. Таким образом, содержание мелких фракций оказывает наиболее значительное влияние на скорость фильтрации и степень очистки по сравнению с другими рассмотренными факторами.
Выводы
Таким образом, можно резюмировать, что на этапе проектирования фильтрационной плотины основное внимание должно быть уделено подбору материала плотины и его гранулометрическому составу, который оказывает наибольшее влияние на скорость фильтрации и степень очистки и который при необходимости должен быть скорректирован для обеспечения требуемых степени очистки и производительности плотины.
Кроме того, можно сделать вывод, что для обеспечения длительной работы наиболее перспективна неоднородная плотина, у которой вдоль направления фильтрации содержание крупных фракций убывает, а мелких – возрастает. В процесса работы такая плотина естественно будет «забиваться», т.е. у нее будет уменьшаться коэффициент пористости и увеличиваться содержание мелких фракций, и, соответственно, будет уменьшаться скорость фильтрации с одновременным увеличением степени очистки, вплоть до ~100 %. При уменьшении скорости фильтрации ниже требуемой придется противодействовать этим эффектам и, в качестве первой меры, надо будет увеличивать разность высот уровней воды в напорной и отводящей траншеях. До некоторой степени эта мера будет работать, однако по достижению максимально возможной разности высот уровней воды в траншеях для увеличения упавшей скорости фильтрации необходимо будет проводить земляные работы по изъятию части конечного участка плотины. Необходимую для изъятия часть плотины можно будет рассчитать с помощью моделирования после определения нового гранулометрического состава поработавшей плотины в нескольких точках вдоль направления фильтрации.
Работа выполнена при финансовой поддержке и в рамках государственного контракта № 14.515.11.0061, ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007–2013 годы» Министерства образования и науки Российской Федерации.
Рецензенты:
Ибламинов Р.Г., д.г.-м.н., профессор, зав. кафедрой минералогии и петрографии ЕНИ, ФГБОУ ВПО «Пермский государственный национальный исследовательский университет», г. Пермь.
Осовецкий Б.М., д.г.-м.н., профессор, профессор кафедры минералогии и петрографии ЕНИ, ФГБОУ ВПО «Пермский государственный национальный исследовательский университет», г. Пермь.
Библиографическая ссылка
Вылков А.И., Удилов А.Е. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ СВОЙСТВ ТЕХНОГЕННЫХ ФИЛЬТРАЦИОННЫХ ПЛОТИН И ПОЛЕЙ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10523 (дата обращения: 16.02.2026).



