Введение
При планировании новых проектов аналитики сталкиваются с проблемой неопределенности, которая для каждой сферы проявляется по-разному. Обычно неопределенность относится к предсказаниям будущих событий, или к неизвестному.
В общем случае, неопределенность - нехватка уверенности, состояние наличия ограниченных знаний, где невозможно точно описать будущий результат или наличие большого числа возможных исходов. В такой ситуации конечно можно использовать классические статистические (вероятностные) методы, но как показывает практика, их использование не всегда может дать адекватные результаты т.к. не всегда существуют условия для их корректного применения, что в свою очередь может привести либо к реализации совершенно неэффективного проекта, либо к его избыточному финансированию.
В результате на сегодняшний день уделяется большое внимание исследованиям в области теории нечетких множеств и в частности нечетким множествам первого порядка (НМ1). В общем виде НМ1 можно определить следующим образом:
![]() , где
, где ![]() ;
; ![]() ,
, ![]() (1)
(1)
где B - базис, X – универсальное множество, ![]() - отображение базиса на универсальное множество.
- отображение базиса на универсальное множество.
Для решения конкретных практических задач определение (1) использовать достаточно неудобно, поэтому Лотфи Заде предложил более удобную интерпретацию НМ1 [5]:
![]() (2)
(2)
где X – универсальное множество, а μA(x) - функция принадлежности элемента х множеству А, являющееся подмножеством универсального множества. На основе нечетких множеств первого порядка были разработаны различные модели и алгоритмы для принятия решения в условиях неопределенности, и в частности модель оценки эффективности инвестиционных проектов [1,2]. Анализ таких методов и моделей показывает, что довольно часто они не обеспечивают получение полностью достоверных решений ввиду недостаточно обоснованного выбора параметров моделирования, а поиск эффективных решений сопровождается значительными временными затратами из-за необходимости выполнения многократных реализаций используемых методов, моделей и алгоритмов с целью выбора оптимальных параметров. Еще одним недостатком нечетких множеств первого порядка является тот факт, что зачастую они не могут адекватно описать всю имеющуюся неопределенность (вероятностную, интервальную, временную).
Средством для решения всех выше описанных проблем могут выступить нечеткие множества второго порядка (НМ2), которые и будут более подробно описаны в этой статье.
Нечеткие множества второго порядка
Нечеткие множества второго порядка являются обобщением нечетких множеств первого порядка и разрабатывались для обработки большей степени неопределенности. Еще в начале исследований, связанных с теорией нечетких множеств, высказывались соображения о том, что функция принадлежности нечеткого множества первого порядка практически не содержит неопределенности, связанной с ней, что, в свою очередь противоречит слову «нечеткий», что означает «много неопределенности».
В таком случае возникает закономерный вопрос: - что делать в той ситуации, когда возникают сомнения относительно значения функции принадлежности. В ответ на этот вопрос был Лотфи А. Заде, предложил использовать более сложные виды нечетких множеств и названные нечеткими множествами второго порядка (НМ2). Они дают возможность описать всю неопределенность в функции принадлежности теории нечетких множеств. Если же неопределенность имеет достаточно низкий уровень, то НМ2 можно свести к НМ1, так же как снижение вероятности к детерминизму, когда неопределенность исчезает.
Исходя из приведенного выше определения НМ1 (1) можно вывести формулу для определения нечеткого множества n-порядка:
![]()
![]() ,
, ![]() , (3)
, (3)
из которого получаем определение НМ2:
![]()
![]() ,
, ![]() ,
, ![]() ;
; ![]() }, (4)
}, (4)
при этом ![]()
![]()
В работе [3] Мендель и Джохан предложили определение более удобное для практического применения:
![]() , (5)
, (5)
где X - универсальное множество, а ![]() – множество функций принадлежности
– множество функций принадлежности ![]() , характеризующих степень принадлежности элементов x и и (третье измерение, характеризующее вторичную функцию принадлежности) множеству A . Различают общее и интервальное НМ2. Особенности каждого вида будут рассмотрены далее.
, характеризующих степень принадлежности элементов x и и (третье измерение, характеризующее вторичную функцию принадлежности) множеству A . Различают общее и интервальное НМ2. Особенности каждого вида будут рассмотрены далее.
Функция принадлежности общего НМ2, представлена в 3-мерной модели на рисунке 1, где третьим измерением функции принадлежности в каждой точке 2-мерной области является так называемый след неопределенности (FOU).
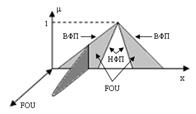
Рисунок 1. След неопределенности НМ2
След неопределенности - это размывание функции принадлежности первого порядка, который полностью описывается двумя ее ограничивающими функциями (рис. 1): нижняя функция принадлежности (НФП) и верхней функции принадлежности (ВФП), каждая из которых представляет собой нечеткое множество первого порядка.
Следовательно, можно использовать нечеткую математику, характерную для первого порядка при работе с НМ2, с особенностями которой можно ознакомиться в статье Менделя и Карника [4].
Сравнение нечетких множеств первого и второго порядков
Нечеткие множества первого порядка характеризуется степенью расплывчатости, а вторые - степенью нечеткости, так что его можно было бы назвать "нечеткое нечеткое множество." Такое множество полезно в тех случаях, когда затруднительно определить точное значение функции принадлежности для нечеткого множества, а так же и при моделировании.
В НМ1 степень принадлежности определена числом, принадлежащим интервалу [0, 1], в НМ2 - степень принадлежности сама по себе нечетка и представляется как вторичная функция принадлежности. НМ2 включают третье измерение и след неопределенности, который дает им дополнительные степени свободы для управления неопределенностью.
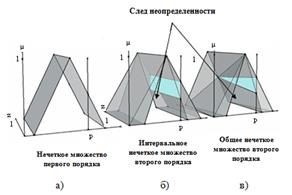
На рис. 2 представлено трех типов нечетких множеств. Нужно отметить, что, в то время как традиционное множество первого типа не визуализируется как трехмерный набор, его концепция и визуализация в трех измерениях, является прямой. При рассмотрении каждого из его элементов, связанного со значением функции принадлежности в третьем измерении равным 1, получаем полную уверенность относительно каждого достигнутого значения принадлежности, связанным с новым входным значением.
НМ1 учитывает нечеткое представление исходного параметра и функция принадлежности этого множества определяет степень принадлежности, полученную на основании исходного набора термов и в результате она перестает быть нечеткой (теряется вся неопределенность). Если же существует достаточный уровень неопределенности в количестве исходных наборов, то можно воспользоваться НМ2, которые дают возможность избежать постоянного обновления функции принадлежности и результата в степенях принадлежности, при этом наличие неопределенности сохраняется, что в некоторых случаях необходимо учитывать [3].
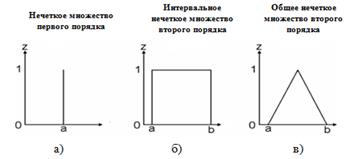
Рисунок 3. Представление вторичных функций принадлежности (третьи измерения)
На рис. 2 представлен исходный параметр p, примененный к трем различным типам нечетких множеств – НМ1 (2а), интервальное НМ2 (2б) и общее НМ2 (2в), на основе которого получаем степени принадлежности (определенной для типа нечеткого множества). Количество неопределенности (и распределение), которое связано со степенью – след неопределенности, выделено цветом в рис. 2 и более наглядно продемонстрировано на рис. 3, котором показаны вторичные функции принадлежности (третье измерение) НМ1 - рис. 3a, интервального НМ2 – рис. 3б и общего НМ2 – рис. 3в. Нужно отметить, что рис. 3 визуализирует µ-z измерения.
У вторичной функции принадлежности НМ1 есть только одно значение в ее области (рис. 3a) в соответствии с основным значением функции принадлежности, в которой вторичность равняется 1. Следовательно, в НМ1, для каждого значения x (в нашем случае p), нет никакой неопределенности, связанной с основным значением функции принадлежности. В интервальном НМ2 (рис. 3б), существует максимальная неопределенность, связанная со вторичной функцией принадлежности, поскольку значение основной функции принадлежности находится в пределах интервала [a, b], где у каждого значения в этом интервале есть связанная с ним вторичная принадлежность 1. Что касается общего НМ2 (рис. 3в), то неопределенность (представление вторичной функцией принадлежности) здесь может быть смоделирована с любой степенью между первым и интервальным вторым нечетким множеством, например треугольной вторичной функцией принадлежности - рисунке 3в. В целом, можно отметить, что общее НМ2 позволяет смоделировать любую степень неопределенности в третьем измерении, т.е. если неопределенность практически отсутствует, то данное НМ2 можно свести к первому порядку, в случае максимального уровня неопределенности все можно свести к интервальному НМ2, где неопределенность одинаково распределена в третьем измерении.
Высоты функции принадлежности второго порядка находятся на вершине своего следа неопределенности. На рис. 4б показан след неопределенности, если существует размывание треугольной функции принадлежности, представленное затенением. Другой пример приведен на рис. 4а для гауссовой первичной функции принадлежности, у которой стандартное отклонение известно с совершенной уверенностью, но, среднее, ??m, не определено и варьируется где-нибудь в интервале от m1 до m2. Равномерное затенение в течение всего следа неопределенности означает, что предполагается равномерное взвешивание (возможности). Из-за равномерного взвешивания, это НМ2 называется интервальным НМ2 (рис. 4б) [3].
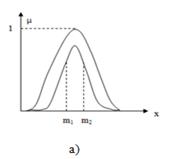
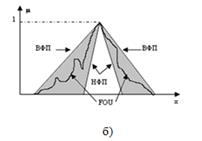
Рисунок 4. Общее (а) и интервальное (б) НМ2
Почти все приложения используют интервальное НМ2, потому что, на сегодняшний день, только для таких множеств (и систем, которые используют их), все расчеты просты для выполнения. Кроме того, хотя общее НМ2 дает больше степеней свободы параметров, чем интервальное, никто не знает еще, что лучше выбрать.
Практическое применение нечетких множеств второго порядка
Для демонстрации целесообразности использования НМ2 рассмотрим актуальную на сегодня проблему – оценка экономической эффективности инвестиционных проектов.
Исходное условие задачи:
Необходимо проанализировать три инвестиционные проекта, реализация которых рассчитана на 5 лет, с различными объемами предполагаемых вложений и доходов. Необходимо определить наиболее эффективный инвестиционный проект с учетом данных представленных в таблице 1 (данные реальные, но обезличенные). Ставка дисконтирования равна 15%, а уровень инфляции составляет 8,3%.
Таблица 1 Исходные данные по задаче
|
Название |
Требуемые инвестиционные вложения, млн. руб. |
Прогнозируемый поток доходов с учетом срока реализации, млн. руб.: |
||||
|
1 |
2 |
3 |
4 |
5 |
||
|
ИП-1 |
150 |
30 |
50 |
70 |
100 |
135 |
|
ИП-2 |
110 |
30 |
40 |
60 |
80 |
100 |
|
ИП-3 |
135 |
20 |
40 |
70 |
90 |
110 |
Для определении наиболее эффективного с экономической точки зрения инвестиционного проекта воспользуемся тремя показателями:
Чистая текущая стоимость – NPV(д. ед.): Индекс рентабельности – PI (д. ед.):
![]() , (6)
, (6) ![]() (7)
(7)
где Сk - доходы в k-й период времени; IC - инвестиционные вложения; r - ставка дисконтирования; i - прогнозируемый средний уровень инфляции.
|
Алгоритм решения на основе НМ1 [2]: |
Алгоритм решения на основе НМ2: |
|
1. Получение экспертных прогнозов о денежных потоках. 2. Преобразование полученных данных в интервальную форму. 3. Выбор ширины интервала приближения для балансового уравнения денежных потоков. 4. Переход к математическому представлению балансового уравнения в виде системы. 5. Вычисление интервальных значений срезов IRR. 6. Восстановление функции принадлежности (для решения задач, возникающих на шагах 5 и 6, используется описанный выше метод решения нечетких интервальных систем). 7. Дефаззификация полученных нечетких результатов. 8. Представление полученного значения IRR в виде графической зависимости. 9. Выбор оптимального решения на основании компромисса между допустимыми рисками и прогнозируемым доходом. |
1. Инициализация — выбор исходной совокупности инвестиционных проектов 2. Задание исходных параметров инвестиционных проектов на основе экспертных оценок с преобразованием их в интервальную форму 3. Выбор вида функции принадлежности 4. Задание параметров функции принадлежности 5. Расчет значений критериев оценки на основе интервальной математики для НМ2 (значения α-срезов FOU) 6. Построение функций принадлежности для каждого ИП (строятся соответствующие пары значений на основе функции random) 7. Дефаззификация полученных нечетких результатов 8. Выделение области нахождения наилучшего (оптимального) решения (использование методов Min и Мах) 9. Нахождение оптимального решения из выбранной области на основании компромисса между допустимыми рисками и прогнозируемым доходом. |
Для эффективного применения приведенных выше алгоритмов, все необходимые расчеты проведем в ПС «FuzzyCalc», которое позволяет учесть возможную неопределенность прогнозных значений по проектам. Следует заметить, что все представленные ниже расчеты приводятся в нечетком виде.
Таблица 2 Решение задачи с помощью алгоритма на основе НМ1:
|
Ставка дисконтирования (r): |
0,15 |
||||||
|
Уровень инфляции (i): |
0.0833431 |
||||||
|
|
ИП-1 |
с i: |
ИП-2 |
с i: |
ИП-3 |
с i: |
|
|
IC: |
150 |
136.433 |
110 |
102.391 |
135 |
124.253 |
|
|
Года: |
Ck |
Ckr |
Ck |
Ckr |
Ck |
Ckr |
|
|
1 |
30 |
26.1709 |
30 |
26.036 |
20 |
17.455 |
|
|
2 |
50 |
36.7485 |
40 |
29.8089 |
40 |
30.3947 |
|
|
3 |
70 |
46.0108 |
60 |
38.8939 |
70 |
46.3037 |
|
|
4 |
100 |
56.7797 |
80 |
45.5995 |
90 |
51.4825 |
|
|
5 |
135 |
66.7563 |
100 |
50.1758 |
110 |
54.2856 |
|
|
Сумма: |
|
232.466 |
|
190.514 |
|
199.921 |
|
|
NPV: |
|
97.6166 |
|
88.6452 |
|
75.8167 |
|
|
PI: |
|
1.52544 |
|
1.71574 |
|
1.43314 |
|
|
NPV: |
PI: |
||||||
µ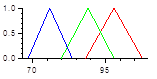 |
µ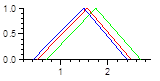 |
||||||
Ckr – дисконтированный поток доходов за k-й период времени
Таблица 3 Решение задачи с помощью алгоритма на основе НМ2:
|
Ставка дисконтирования (r): |
0,15 |
||||||
|
Уровень инфляции (i): |
0.0833431 |
||||||
|
|
ИП-1 |
с i: |
ИП-2 |
с i: |
ИП-3 |
с i: |
|
|
IC: |
150 |
136.433 |
110 |
102.391 |
135 |
124.253 |
|
|
Года: |
Ck |
Ckr |
Ck |
Ckr |
Ck |
Ckr |
|
|
1 |
30 |
26,12103 |
30 |
26,12103 |
20 |
17,41402 |
|
|
2 |
50 |
37,906 |
40 |
30,3248 |
40 |
30,3248 |
|
|
3 |
70 |
46,20671 |
60 |
39,60575 |
70 |
46,20671 |
|
|
4 |
100 |
57,47461 |
80 |
45,97968 |
90 |
51,72715 |
|
|
5 |
135 |
67,55831 |
100 |
50,04319 |
110 |
55,04751 |
|
|
Сумма: |
|
235,2667 |
|
192,0745 |
|
200,7202 |
|
|
NPV: |
|
96,6806 |
|
90,44469 |
|
75,99274 |
|
|
PI: |
|
1,568444 |
|
1,746131 |
|
1,486816 |
|
|
NPV: |
PI: |
||||||
µ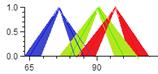 |
µ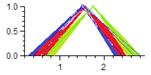 |
||||||
Исходя из полученных результатов, можно сделать вывод о том, что с точки зрения рассмотренных показателей ИП-3 менее эффективный, соответственно из дальнейшего анализа его можно исключить. Следовательно, далее будем рассматривать только первый и второй инвестиционный проекты, поскольку на данном этапе нельзя однозначно определить наиболее эффективный с экономической точки зрения. Поскольку было представлено решение как на основе НМ1, так и на основе НМ2, логично продолжить решение в обоих случаях, но это возможно лишь с помощью НМ2 так как НМ1 не обладают достаточными возможностями для дальнейшего решения задачи.
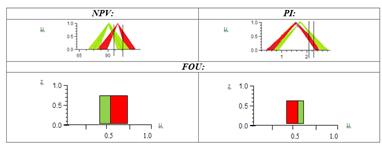
Как уже говорилось ранее НМ2 имеют третье измерение, так называемый след неопределенности (FOU) и именного его и следует использовать для нахождения окончательного решения:
Полученные выше результаты представим как вероятность получения соответствующих значений показателей NPV и PI – 0,73 и 0,62. Тогда использую формулу полной вероятности рассчитаем вероятность реализации как ИП-1, так и ИП-2:
![]() (8)
(8)
![]()
![]()
Исходя из полученных расчетов FOU для каждого из двух оставшихся на этом этапе проектов, можно сделать вывод о том, что выгоднее и экономически рентабельнее будет выбрать ИП-1.
Что же касается предлагаемой модели оценки инвестиционных проектов на основе нечетких множеств второго порядка, то данная модель предполагает решения актуальной на сегодняшний день задачи финансового бюджетирования в условиях неопределенности, основанная на нечеткой параметризации исходных данных. Используя полученный алгоритм, можно рассчитать требуемые показатели экономической эффективности инвестиционных проектов и по совокупности (что иногда бывает затруднительно при использовании НМ1) определить наиболее выгодный как для инвестора, так и для руководителя.
Рецензенты:
Чернов В.Г., д.э.н., профессор кафедры Управление и информатика в технических и экономических системах ВлГУ, г.Владимир.
Дубровин Н.И., д.ф.м.н., профессор, заведующий каф. Алгебра и геометрия ВлГУ, г.Владимир.
Библиографическая ссылка
Ремезова Е.М. НЕЧЕТКИЕ МНОЖЕСТВА ВТОРОГО ПОРЯДКА: ПОНЯТИЕ, АНАЛИЗ И ОСОБЕННОСТИ ПРИМЕНЕНИЯ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10506 (дата обращения: 27.02.2026).



