Введение
В существующей теории моделирования дорожно-грунтовых оснований (ДГО) распределяли их по величине неровностей, а именно по частоте и амплитуде, наряду с корреляционной функцией и спектральной плотностью. Однако как показали исследования, то важным при составлении характеристик является характер неровностей. В большинстве случаев, при решении задач плавности хода автомобиля задаются возмущающим воздействием в виде суммы гармоник или «белого шума» со спектральной плотностью (корреляционной функцией) характерной для исследуемого участка. Но как показывает практика, это не всегда верно. Есть случаи, когда микропрофиль (микрорельеф) ДГО целесообразнее представлять в виде ряда характерных неровностей. Примером могут служить лесные дороги, разбитое асфальтированное шоссе, дороги типа «stone-road». Необходимо отметить, что в работе [10] по описанию неровностей для разбитых асфальтобетонных шоссе приводятся данные о числе выбоин, но только в табличном виде, поэтому эти данные тяжело задать в математической модели
Математическая модель
Анализ неровностей «пороговых (протяженных по отношению в колее машины)» препятствий ДГО позволил выделить основные типы. Они приведены на рис 1.
а б
б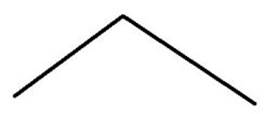
в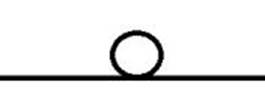 г
г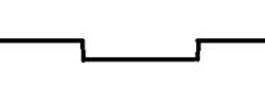
Рис. 1. Характерные профильные «пороговые» препятствия: а – волна, б – треугольник, в – цилиндр, г – выбоина.
Препятствие типа «волна» характерно для большинства естественных ДГО и дорог с усовершенствованным покрытием, для которых характерно интенсивное (или достаточно постоянное для грунтовых дорог) движение. Препятствие типа «треугольник» характерно для естественных ДГО, например поле, для которых характерны единичные случаи движения. Препятствие типа «цилиндр» - это либо лесные дороги, либо дороги типа «stone-road». Препятствие типа «выбоина» - это разбитое асфальтобетонное шоссе.
Множественные исследования авторов статьи позволили предложить следующую теорию.
В результате замеров дорог были получены распределения числа неровностей от их протяженности.
Для математического моделирования наиболее подходящим является показательный (экспоненциальный) закон распределения.
Применительно к зависимости числа неровностей от их протяженности, а также размеров между неровностями:
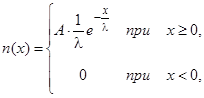 (1)
(1)
где ![]() ,
, ![]() – параметры данного распределения,
– параметры данного распределения, ![]() – шаг дискретизации размеров неровностей.
– шаг дискретизации размеров неровностей.
Рассмотрим примеры (рис. 2) ДГО и характерные неровности на примере трех типов: лесные дороги [5, 6], разбитое асфальтированное шоссе [7], дороги типа «stone-road» [2-4, 9].
а  б
б 
в 
Рис. 2 Примеры ДГО и характерные неровности: а - лесные дороги, б - разбитое асфальтированное шоссе, в - дороги типа «stone-road».
Рассмотрим более подробно для каждого из рассматриваемых типов ДГО, как будут распределяться неровности.
а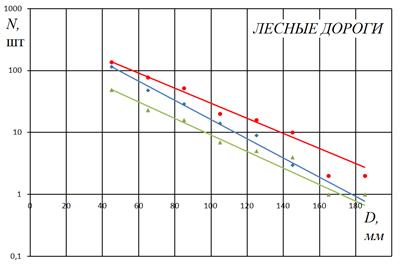
б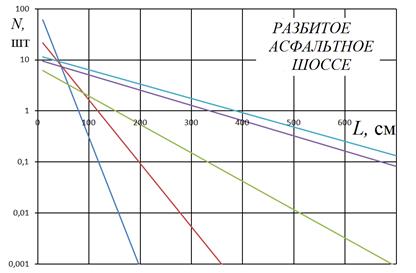
в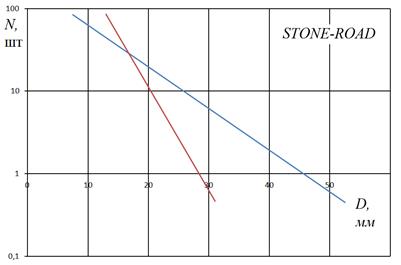
Рис 3. Распределение неровностей на километр пути: а - лесные дороги, б - разбитое асфальтированное шоссе, в - дороги типа «stone-road».
Необходимо отметить, что к аналогичным выводам (закону распределения неровностей) приходят авторы работ по исследованию лунной поверхности, а именно распределению камней и кратеров на поверхности Луны [1, 8].
Для моделирования микропрофиля пути также необходимо знать взаимное расположение характерных неровностей. Проведенные исследования показали, что для этого также можно использовать зависимость (1). Для дорог типа «stone-road» полагаем, что камни расположены рядом друг с другом, поэтому считаем, что расстояние между ними равно нулю. На практике же они могут отстоять на некоторое расстояние, но в данной работе этот случай не исследовался.
Рассмотрим, как для разбитых асфальтных и лесных дорог будут распределяться расстояния между неровностями.
а 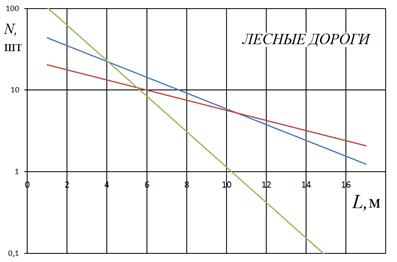
б 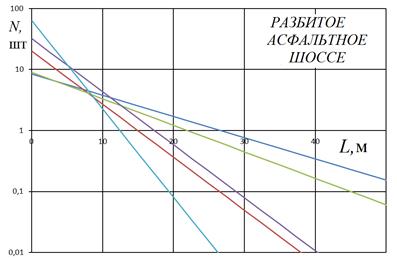
Рис 4. Распределение расстояний между неровностями на километр пути: а - лесные дороги, б - разбитое асфальтированное шоссе.
Рассмотрим более подробно асфальтированные дороги. На основании анализа экспериментальных данных были сделаны следующие выводы, что все множество дорог можно разделить на четыре типа по степени изношенности: ровная, малоизношенная, сильноизношенная и разбитая дорога. Было принято, что для описания асфальтобетонного основания городских дорог можно принять следующие усредненные зависимости, приведенные в таблице 1. Данные значения являются результатом многомерного анализа проведенного авторами работы. Также в таблице приведены характеристики взаимного распределения трещин.
Таблица 1. Параметры модели изношенности для различных участков дорог
|
№ п.п. |
Характеристика дороги |
Тип неровностей |
Параметры размеров |
Параметры расстояний между |
Средняя глубина неровности, см |
||
|
|
|
|
|
|
|||
|
1 |
Ровная дорога |
Выбоины |
- |
- |
- |
- |
- |
|
Трещины |
- |
1 |
180 |
5 |
- |
||
|
2 |
Малоизношенная |
Выбоины |
185* |
15 |
100 |
15 |
1 |
|
Трещины |
- |
2 |
120 |
5 |
- |
||
|
3 |
Сильноизношенная |
Выбоины |
100* |
45 |
110 |
6 |
2 |
|
Трещины |
- |
3 |
60 |
5 |
- |
||
|
4 |
Разбитая дорога |
Выбоины |
190* |
150 |
190 |
5 |
3 |
Как видно из таблицы значения, приведенные в ней, говорят о том, что для «ровной дороги», «малоизношенной» и «сильноизношенной» характерно наличие трещин. При этом можно использовать только зависимость взаимного распределения расстояний между трещинами, а размеры брать постоянными. Получается, что на «ровной» дороге трещин больше, а на «сильноизношенной» меньше, но они шире. В свою очередь на разбитой дороге их можно не учитывать, так как в данном случае трещины уже «переродились» в выбоины.
Интересное явление наблюдается для изменения на «малоизношенной», «сильноизношенной» и «разбитой» дорогах. При увеличении разбитости увеличивается протяженность неровностей и их средняя глубина, и как следствие расстояния между неровностями.
Выводы
- Приведена классификация профильных «пороговых» препятствий дорожно-грунтовых оснований.
- Впервые получены зависимости для описания числа характерных неровностей и их взаимного расположения для разных дорог, таких как лесная дорога, разбитое асфальтированное шоссе, дорога типа «stone-road».
- Приведена классификация асфальтобетонного основания городских дорог в зависимости от степени его изношенности. Даны коэффициенты для расчета параметров распределения неровностей и их взаимного расположения.
- Используя полученные данные можно спрогнозировать плавность хода транспортно-технологических машин на опорных основаниях рассмотренного типа из условий подвижности по мобильности с ограничением движения по профильной проходимости.
- Полученные законы распределения неровностей характерны не только Земных условий, но и для описания поверхностей движения космических тел, в частности Луны.
Исследования проведены при финансовой поддержке Министерства образования и науки РФ в рамках проекта по договору № 02.G25.31.0006 от 12.02.2013 г. (постановление Правительства Российской Федерации от 9 апреля 2010 года №218).
Рецензенты:
Молев Ю.И., д.т.н., профессор кафедры «Строительные и дорожные машины» ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е.Алексеева», г. Нижний Новгород.
Шапкин В.А., д.т.н., профессор кафедры «Строительные и дорожные машины» ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е.Алексеева», г. Нижний Новгород.
Библиографическая ссылка
Макаров В.С., Зезюлин Д.В., Беляев А.М., Зубов П.П., Вахидов У.Ш., Редкозубов А.В., Беляков В.В. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОВЕРХНОСТИ ДОРОЖНО-ГРУНТОВЫХ ОСНОВАНИЙ, НАСЫЩЕННЫХ ХАРАКТЕРНЫМИ ПОВТОРЯЮЩИМИСЯ ДИСКРЕТНЫМИ ПРЕПЯТСТВИЯМИ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10472 (дата обращения: 17.02.2026).



