В Стратегии модернизации российского образования, в Законе РФ «Об образовании», Национальной доктрине образования в РФ до 2025 г. и других правительственных документах по образованию главная задача российской образовательной политики сформулирована как обеспечение современного качества образования на основе сохранения его фундаментальности и соответствия актуальным и перспективным потребностям личности, общества и государства.
Одной из проблем повышения качества обучения является проблема разработки критериев и показателей качества знаний, умений и навыков; разработка модели внутривузовского контроля за качеством подготовки специалистов. Больше всего исследований посвящено разработке критериев и показателей качества образования и проблеме оценивания знаний и умений. Так И.Я. Лернером выделена система свойств (показателей), «качеств знания», характеризующая полноценность знаний учащихся общеобразовательных школ: полнота, глубина, точность, осознанность, системность, систематичность, прочность, оперативность, гибкость, действенность [3].
Во время обучения в педвузе студенту необходимо усвоить достаточно большой объем профессиональных знаний и умений. Математические и методические знания и умения, составляющие основную часть профессиональных умений учителя математики, должны обладать такими качествами как осмысленность и прочность. Но, практика показывает, что знания и умения студентов в основном не обладают такими качествами, утрачиваются полностью или частично. Нужна система повторения математических и методических дисциплин в педвузе.
В теории и методике обучения математике в школе сложилась определенная система повторения. В теоретических исследованиях хорошо изучены и в практике обучения математике в школе используются различные виды повторения, методические особенности их содержания, организации и т. п.
В исследовании Г.К. Безруковой [1], разработана технология проектирования повторительной работы по математике в школе. Г.К. Безрукова уточняет понятие повторения, которое мы положили в основу данного исследования: повторение – это воспроизведение и последующее совершенствование ранее усвоенной информации с целью ее использования на качественно ином уровне работы с системой знаний. Система процедур технологии В.М. Монахова дополнена новыми, характерными для повторения процедурами: а) проектирования целеполагания для двух видов (сопутствующее и обобщающее повторение «для чего повторять?»); б) встраивания повторительной работы в логическую структуру учебного содержания («сколько и в какой мере повторять?»); в) установления соответствия между целеполаганием и качеством повторительной работы.
В.А. Тестов считает, что в педвузе организации повторения математики должно способствовать, прежде всего, само построение математических курсов, учитывающее многоступенчатость и преемственность формирования математических структур. Спиралевидное построение программы математических дисциплин (в школе и в вузе) позволяет естественным образом проводить повторение на более высокой ступени математических структур, устанавливать связи между старыми знаниями: изучение темы не исчерпывается во всех деталях сразу же в течение одного учебного года, а желательно возвращение к каждой теме с более богатым содержанием [5].
При изучении математических и методических дисциплин в высшей школе повторение практически отсутствует как в образовательных стандартах и программах, так и в практике обучения. В то же время особенности обучения в вузе (большой объемом информации, редкий контроль усвоения знаний и способов деятельности и др.) порождают трудности в учебной деятельности студентов, которые влияют на результаты обучения (на качество знаний и умений).
Повторение изученного материала должно осуществляться в определенной системе, которая встроена в методическую систему изучения элементарной математики, теории и методики обучения математике [6]. Требования к проектированию повторения элементарной математики, теории и методики обучения математике разработаны на основе анализа психолого-педагогических и методических исследований проблемы повторения с позиций технологического подхода к обучению (О.Б. Епишева [2], Монахов В.М. [4] и др.).
I. Общие цели повторения проектируются по категориям знание, понимание, умения и выражаются в действиях студентов и конкретизируются на отобранном для повторения материале.
Общие цели повторения:
Студент знает и понимает:
- место и роль будущей информации (по элементарной математике и методике обучения математике) в системе уже имеющихся знаний;
- приемы запоминания и восстановления в памяти плохо усвоенных или забытых знаний и способов деятельности;
- приемы установления логических связей между изученным материалом и материалом, изучить который предстоит;
умеет:
- выделять основной материал в ранее изученном, систематизировать и обобщать его;
- совершенствовать ранее усвоенные понятия и способы действий.
- рассматривать и преобразовывать материал школьного курса математики (элементарной математики) глазами учителя.
Ниже приведены конкретизированные цели повторения содержательно-методической линий школьного курса арифметики и алгебры «Числа и вычисления».
Студент знает и понимает:
- основную идею развития понятия числа и расширения числовых множеств;
- основные арифметические понятия, их определения;
- методику обучения математическим понятиям в школе;
- правила вычислений и различные способы (в том числе наиболее рациональные) их формулировки;
- основные этапы и приемы обучения правилам вычислений;
- основные типы арифметических задач школьного курса математики;
- основные этапы, методы, алгоритмы и приемы решения арифметических задач;
умеет:
- определять, классифицировать, сравнивать, символически записывать числовые множества, их свойства и правила действий с числами;
- планировать методику обучения числовым множествам;
- применять правила вычислений, решать арифметические задачи различными методами;
- на основе общего методического приема планировать методику обучения решению арифметических задач.
III. Содержание повторения спроектировано в соответствии с целями повторения.
Компоненты содержания повторения: 1) теоретический, состоящий из математического содержания (элементарная математика) и методического содержания (курс общей и специальной методики обучения математике); 2) практический, состоящий из учебных задач и математических задач для повторения.
Основные типы математических и учебных задач для повторения по классификации несколько отличаются от основных типов задач для изучения основного курса (задачи на формирование знания, понимания изучаемого, задания на формирование умений и навыков, задачи на достижение развивающих и воспитательных целей), т.к. они должны отражать и специфические цели повторения. Нами выделены следующие типы задач для повторения:
1) задачи на воспроизведение изученного ранее школьного и вузовского материала;
2) задачи на обобщение и систематизацию изученного материала;
3) задачи на развитие памяти, внимания и мышления (на изученном материале);
4) задачи на установление связей элементарной математики с методикой обучения математике;
Все математические, методические и учебные задачи для повторения дифференцированы по уровням усвоения (учебной деятельности) студентов.
Математические и учебные задачи для повторения разработаны нами, с учетом целей повторения, на материале школьного курса математики, материале курса общей методики и изучаемой специальной методики обучения математике в основной школе. Содержательная конкретизация обобщенных типов задач для повторения представлена в виде системы учебных заданий, которые выполняют студенты в процессе повторения и обучения. Учебные и математические задачи 1-го типа (на воспроизведение изученного) выполняют функцию актуализации ранее изученных знаний для дальнейшего изучения курса. Учебные и математические задачи остальных типов (на обобщение и систематизацию, на развитие памяти, на установление логических связей) реализуют обогащающий характер повторения.
Ниже приведены примеры таких учебных заданий для повторения содержательно-методической линии «Числа и вычисления».
1) Задания на воспроизведение ранее изученного школьного курса математики и курса общей методики преподавания математики
На 1-м уровне это означает, что студент воспроизводит простейшие понятия, термины, свойства чисел и вычислений, символическую запись, общие методы решения математических задач и т. п.; основные положения общей методики обучения математики.
1. Определите, какое из данных утверждений ошибочное:
а) произведение равно нулю, если хотя бы один из множителей равен нулю;
б) если число делится одновременно на 2 и 8, то оно делится на 16;
в) при умножении степеней с одинаковыми основаниями показатели складываются, а основание остается прежним;
г) частное обыкновенной дроби и натурального числа равно дроби с тем же числителем и знаменателем, равным произведению знаменателя данной дроби и натурального числа.
На 2-м уровне студент воспроизводит определения понятий, формулировки правил (алгоритмов) школьного курса математики, методы решения арифметических задач, способы устных вычислений, методику работы над понятиями, методику работы над задачей и т.д.
1. Вычислите: 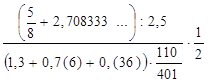
На 3-м уровне студент воспроизводит основные направления специальной методики изучения числовой линии, приемы рациональных вычислений и др.
1. Вычислите ![]() и укажите верный ответ среди предложенных:
и укажите верный ответ среди предложенных:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2. Вычислите устно: 99 + 95 + 91 + … + 7 + 3 – 1 – 5 – … – 89 – 93 – 97.
2) Задания на обобщение и систематизацию изученного материала
На 1-м уровне это означает, что обобщение и систематизация происходит на уровне понятий, т.е. студент выделяет существенные признаки понятий, подводит объект под понятие, выделяет методы и методические приемы работы с понятиями, правилами и задачами числовой линии.
1. Определите, является ли данное утверждений верным: сумма любых двух рациональных чисел – рациональное число.
На 2-м уровне обобщение и систематизация происходит на уровне системы понятий, т.е. студент сопоставляет, сравнивает данные понятия, выделяет на этой основе существенные свойства, сравнивает методику изучения понятий, правил, методику обучения решению арифметических задач с общей методической схемой обучения решению математических задач и др.
1. Сравните традиционный и технологический подход к проектированию целей обучения математике. Сделайте выводы.
На 3-м уровне обобщение и систематизация происходит на уровне теории, т.е. при выполнении этих заданий студент обобщает и систематизирует изученные теоретические положения.
1. Найдите, в каких других задачах (или других темах) используются похожие приемы решения задач по теме «Обыкновенные дроби». Обобщите их.
3) Задания на развитие памяти, внимания и мышления
На развитие памяти
1. Назовите основные термины темы «Дроби» (5-6-ой класс), начинающиеся на одну и ту же букву.
На развитие внимания
1. Ответ на вопросы задачи необходимо выбрать из следующих чисел: 0,2 г; 250 м; 1,435 м; 45 см; 1,2 л; 0,6.
а) Чему равна высота стула (от пола до сиденья)?
б) Назовите примерно ширину железнодорожной колеи (расстояние между рельсами).
в) На каком расстоянии можно различать цвет одежды человека?
На развитие мышления
1. Продолжите числовую последовательность 2, 5, 7, 11, 14, …
4) Задания на установление связей между элементарной математикой и методикой ее изучения
На 1-м уровне студент выделяет понятия, вновь вводимые в данной теме, устанавливает вид определения и его структуру, формулирует вопросы для учащихся с целью раскрытия структуры определения и его применения. Студент, зная логическую структуру определения понятия, продумывает методику работы над структурой и над усвоением определения понятия. Аналогично для алгоритмов и правил числовой линии.
1. Сформулируйте для учащихся 6-го класса вопросы на усвоение структуры определения понятия «координатная прямая».
На 2-м уровне студент выделяет основные методы решения арифметических задач и выделяет основные действия учащихся по их решению, формулирует приемы их решения, составляет учебные задачи для формирования умений решать задачи данного типа.
1. Выделите действия учащихся по нахождению модуля числа. Составьте учебные задачи на каждое действие.
На 3-м уровне студент выделяет общие идеи и методы изучения числовой линии, основные методы решения арифметических задач, разрабатывает методику изучения числовой линии в школе.
1. Найдите в учебнике «Математика 6» (авт. В.Я. Виленкин и др.) основную идею расширения множества рациональных неотрицательных чисел до множества всех рациональных чисел.
2. Составьте план работы с учащимися по изучению множества положительных и отрицательных чисел.
IV. Проектирование методов, средств и форм повторения. Основным методом повторения элементарной математики, теории и методики обучения математике является самостоятельное решение специально подобранных математических и учебных задач для повторения. Решение задач является важнейшим видом учебной деятельности, в процессе которого студенты приобретают новые знания, умения и способы деятельности, совершенствуют и углубляют их. Другим основным методом повторения является обсуждение в группе или индивидуально с преподавателем результатов выполнения специальных математических и учебных задач для повторения. При этом задача преподавателя – помочь студенту выявить трудности, возникающие при повторении; дать необходимые рекомендации для повторения и преодоления этих трудностей; помощь в планировании и осуществлении повторения; консультация в выполнении специальных заданий для повторения. Средствами повторения являются учебно-методическая и справочная литература: учебники, в том числе и школьные, учебные пособия; средства наглядности: таблицы, схемы, презентации и т.п. Кроме этого, к средствам повторения мы относим комплекс учебных пособий по руководству самостоятельной работой студентов. Например, учебное пособие «Руководство для повторения курса «Элементарная математика, теория и методика обучения математике», представленное в двух вариантах: печатном и электронном.
V. Проектирование диагностики и оценки результатов повторения осуществляется в трех формах: а) самоконтроль студентами результатов усвоения при повторении с помощью электронного варианта пособия; б) контроль преподавателем результатов повторения с помощью электронного варианта пособия; в) контроль преподавателем результатов повторения на семинарско-практических занятиях и их дальнейшая коррекция.
Математические и учебные задачи на диагностику результатов повторения адекватны задачам на диагностику результатов изучения основного курса.
1-й уровень
1. Заполните пропуски так, чтобы получилось верное утверждение:
1) Дробь 0,025, представленная как обыкновенная несократимая дробь, равна …
3) ![]() = …
= …
2-й уровень
1. Производительность труда понижалась 2 раза в год на одно и то же число процентов. Найдите это число, если выработка снизилась с 2000 руб. до 1767,2 руб.
2. Отметьте, какой из названных методических приемов используется на заключительном этапе работы над арифметической задачей:
а) проверка результатов решения задачи; б) обоснование правильности решения;
в) составление аналогичной задачи; г) составление плана решения задачи.
3-й уровень
1. Установите, какая из ниже перечисленных учебных задач направлена на развитие логического мышления учащихся:
а) запишите все делители чисел: 18, 24, 45.
б) сравните числа 0,52 и 13/23.
в) в следующем определении подчеркните термин волнистой чертой, родовое понятие – одной прямой чертой, видовое отличие – двумя прямыми чертами: числа, которые можно записать в виде обыкновенной дроби, называются рациональными.
г) запишите под диктовку следующие числа: 0,098; ¼, 5,075; 3,448.
Статья выполнена в рамках финансирования долгосрочной целевой программы «Основные направления образования и науки Тюменской области
Рецензенты:
Епишева Ольга Борисовна, доктор пед. наук, профессор кафедры математики, теории и методики обучения математике федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Тобольская государственная социально-педагогическая академия им. Д.И. Менделеева».
Маллабоев Умарджон, доктор физ.-мат. наук, профессор кафедры физики, технологии и методик преподавания федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Тобольская государственная социально-педагогическая академия им. Д.И. Менделеева».
Библиографическая ссылка
Шебанова Л.П. ПРОЕКТИРОВАНИЕ ПОВТОРЕНИЯ ПРИ ИЗУЧЕНИИ МЕТОДИКИ ОБУЧЕНИЯ МАТЕМАТИКЕ КАК СРЕДСТВА ОБЕСПЕЧЕНИЯ КАЧЕСТВА ПОДГОТОВКИ УЧИТЕЛЯ МАТЕМАТИКИ В ПЕДАГОГИЧЕСКОМ ВУЗЕ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10437 (дата обращения: 17.02.2026).



