Введение
Интенсивно развивающаяся сфера информационных технологий в настоящее время открывает широкие перспективы для развития многих областей науки и техники, что находит свое отражение в нормативно-правовых и законодательных актах РФ. Приоритетными являются направления по созданию единого информационно-телекоммуникационного пространства органов государственного, военного управления, МВД, МЧС и т.д., интегрированной федеральной сети передачи данных, внедрение систем мониторинга, учета и прогнозирования во все сферы деятельности.
Реализация данных направлений возможна на базе создания единой информационно-телекоммуникационной системы (ИТКС), связывающей органы государственной власти, министерства и ведомства.
Однако следует отметить, что устойчивое функционирование такой сложной системы неразрывно связано с обеспечением ее структурной и функциональной живучести. Поиск путей обеспечения высокого уровня живучести требует постановки и решения ряда сложных научно-технических задач. И если исследование структурной составляющей живучести в основном сводится к выявлению уязвимых мест в топологии системы и определению степени их влияния на целостность системы, то исследование функциональной составляющей живучести приводит к определению способности системы решать стоящие перед ней задачи в условиях структурной деградации.
Вместе с тем непредсказуемость изменения большинства воздействующих факторов, влияющих на свойства ИТКС и ее топологию, придает особое значение анализу функциональной составляющей живучести с учетом состояния элементов системы и действующих между ними взаимосвязей. При этом под воздействующими факторами могут пониматься ошибки операторов, физические и программно-аппаратные воздействия злоумышленников и любые деструктивные воздействия, приводящие к структурной деградации системы.

Рис.1. Периоды активной работы элементов ИТКС
Один из путей решения этой задачи лежит в плоскости управления резервными элементами (РМ) ИТКС в процессе диспетчирования вычислительного процесса с учетом ресурсно-временных характеристик на каждой из стадий выполнения плана вычислительного процесса (ПВП).
На рисунке 1 показан фрагмент временной диаграммы при выполнении m-го задания с основными периодами активной работы элементов ИТКС.
МОДЕЛЬ ОРГАНИЗАЦИИ РАСПРЕДЕЛЕННЫХ ВЫЧИСЛЕНИЙ
Математическая модель распределенных вычислений представляет собой зависимость:
![]()
где ![]() – вычислительная структура,
– вычислительная структура,
![]() – расписание, определяющее загрузку вычислительных модулей,
– расписание, определяющее загрузку вычислительных модулей,
![]() – множество деструктивных воздействий по элементам вычислительной структуры.
– множество деструктивных воздействий по элементам вычислительной структуры.
Время ![]() выполнения ПВП в этом случае складывается из времени
выполнения ПВП в этом случае складывается из времени ![]() ожидания поступления g-йстадии m-го задания в обработку, времени
ожидания поступления g-йстадии m-го задания в обработку, времени![]() обработки g-й стадии m-го задания i-м вычислительным модулем (ВМ) и времени
обработки g-й стадии m-го задания i-м вычислительным модулем (ВМ) и времени![]() , затрачиваемого на передачу результатов обработки g-й стадии от i-го к j-му ВМ для обработки (g+1)-й стадии:
, затрачиваемого на передачу результатов обработки g-й стадии от i-го к j-му ВМ для обработки (g+1)-й стадии:
![]() . (1)
. (1)
Время ожидания поступления g-й стадии m-го задания в обработку в общем случае зависит от времени ![]() подготовки i-го ВМ к обработке g-й стадии m-го задания и времени
подготовки i-го ВМ к обработке g-й стадии m-го задания и времени![]() ожидания поступления m-го задания в обработку:
ожидания поступления m-го задания в обработку:
![]() . (2)
. (2)
Необходимо отметить, что значения величин, входящих в выражение (2), являются функцией от расписания ![]() загрузки ВМ [1,4], а также соотношения между количеством заданий M, подлежащих обработке, и величиной выделяемого вычислительного ресурса
загрузки ВМ [1,4], а также соотношения между количеством заданий M, подлежащих обработке, и величиной выделяемого вычислительного ресурса ![]() (количества ВМ):
(количества ВМ):
![]() . (3)
. (3)
При этом если значение ![]() , то значения
, то значения ![]() , если данное соотношение выполняется для любых смежных стадий ПВП, то
, если данное соотношение выполняется для любых смежных стадий ПВП, то ![]() .
.
Для сформированного расписания загрузки ВМ начальные моменты ![]() времени поступления g-й стадии m-го задания в обработку, начальные моменты
времени поступления g-й стадии m-го задания в обработку, начальные моменты ![]() времени передачи результатов обработки определяются из соотношений (4) и (5) соответственно, а допустимый
времени передачи результатов обработки определяются из соотношений (4) и (5) соответственно, а допустимый ![]() резерв времени из соотношения (6):
резерв времени из соотношения (6):
![]() , (4)
, (4)
![]() , (5)
, (5)
![]() , (6)
, (6)
где ![]() – директивное время завершения обработки m-го задания;
– директивное время завершения обработки m-го задания;
![]() – расчетное время завершения обработки m-го задания.
– расчетное время завершения обработки m-го задания.
Модель деструктивных воздействий [3, 6] представлена множеством ![]() , где
, где ![]() – показатель деградации i-го элемента,
– показатель деградации i-го элемента, ![]() – показатель деградации канала связи между i-м и j-м элементами,
– показатель деградации канала связи между i-м и j-м элементами,![]() – момент времени проведения деструктивных воздействий. При этом показатели деградации определяются как:
– момент времени проведения деструктивных воздействий. При этом показатели деградации определяются как:![]() –воздействие по элементу системы отсутствует,
–воздействие по элементу системы отсутствует,![]() – ухудшение характеристик элемента системы,
– ухудшение характеристик элемента системы,![]() – элемент системы выведен из строя.
– элемент системы выведен из строя.
Таким образом, в результате деструктивных воздействий в момент времени ![]() , прогнозируемое время
, прогнозируемое время ![]() , затрачиваемое на обработку g-й стадии m-го задания i-мВМ, будет определяться из выражения (7):
, затрачиваемое на обработку g-й стадии m-го задания i-мВМ, будет определяться из выражения (7):
![]() , (7)
, (7)
а прогнозируемое время передачи результатов обработки по каналу связи от i-го к j-му ВМ из выражения (8) соответственно:
![]() . (8)
. (8)
Из анализа выражений (6), (7) и (8) можно сделать вывод, что условием успешного выполнения задач по предназначению системой будет выполнение условия (9):
![]() , (9)
, (9)
Таким образом, для обеспечения требуемого уровня функциональной живучести [3, 6] ИТКС, необходимо минимизировать значения ![]() временных потерь, возникающих в результате деструктивных воздействий. С этой целью все вычислительные средства ИТКС разбиваются на подмножества основных средств, обеспечивающих непосредственное решение задач по предназначению, и резервных, обеспечивающих живучесть системы [5].
временных потерь, возникающих в результате деструктивных воздействий. С этой целью все вычислительные средства ИТКС разбиваются на подмножества основных средств, обеспечивающих непосредственное решение задач по предназначению, и резервных, обеспечивающих живучесть системы [5].
При этом на резервных вычислительных модулях (РМ) производится мультипрограммная обработка копий заданий, соответствующих загрузке основных ВМ. При отказе одного из основных ВМ, один из РМ прекращает мультипрограммную обработку и переходит к монопольной обработке задания, выполняемого отказавшим ВМ [2]. С целью сокращения задержки ![]() в обработке задания отказавший ВМ замещается тем РМ, на котором задание, выполняемое в момент отказа ВМ, выполнялось больше времени. Таким образом, время выполнения g-й стадии m-го задания на РМ будет определяться из соотношения (10):
в обработке задания отказавший ВМ замещается тем РМ, на котором задание, выполняемое в момент отказа ВМ, выполнялось больше времени. Таким образом, время выполнения g-й стадии m-го задания на РМ будет определяться из соотношения (10):
![]() , (10)
, (10)
где ![]() – квант времени, выделяемый на выполнение копийg-й стадии m-го задания, выполняемого на i-м ВМ в момент времени
– квант времени, выделяемый на выполнение копийg-й стадии m-го задания, выполняемого на i-м ВМ в момент времени![]() .
.
В случае замещения основного канала связи резервным, время передачи результатов обработки будет определяться из выражения (11):
![]() (11)
(11)
где ![]() – объем выходной информации при обработке g-й стадии m-го задания,
– объем выходной информации при обработке g-й стадии m-го задания,
![]() – пропускная способность канала связи между i-м и j-м ВМ,
– пропускная способность канала связи между i-м и j-м ВМ,
![]() – пропускная способность резервного канала связи между i-м и j-м ВМ.
– пропускная способность резервного канала связи между i-м и j-м ВМ.
Таким образом, модель организации распределенных вычислений в условиях деградации вычислительной структуры может быть представлена следующим образом (рисунок 2).
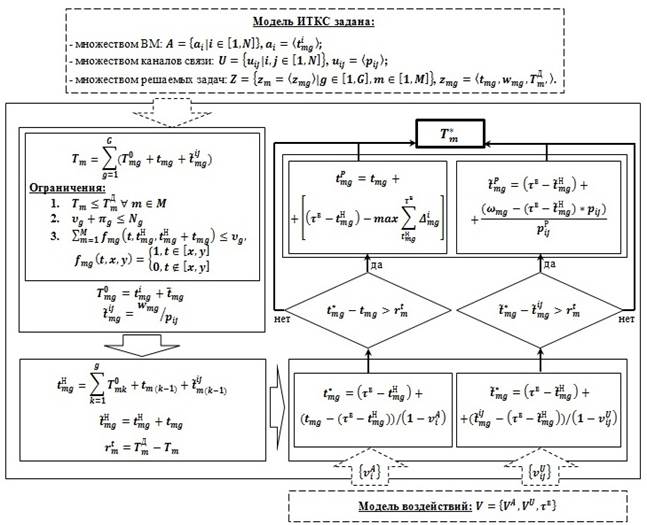
Рис. 2. Модель организации распределенных вычислений в условиях деградации вычислительной структуры
Заключение
Предложенная модель может быть использована для анализа и оценивания эффективности диспетчирования распределенных вычислений в информационно-телекоммуникационных системах, функционирующих в условиях деградации вычислительной структуры.
Рецензенты:
Басыров А. Г., д.т.н., доцент, начальник кафедры информационно-вычислительных систем и сетей Военно-космической академии имени А. Ф. Можайского, г. Санкт-Петербург.
Петренко С. А., д.т.н., доцент, начальник кафедры математического и программного обеспечения Военно-космической академии имени А. Ф. Можайского, г. Санкт-Петербург.
Библиографическая ссылка
Шушаков А.О. МОДЕЛЬ ОРГАНИЗАЦИИ РАСПРЕДЕЛЕННЫХ ВЫЧИСЛЕНИЙ В УСЛОВИЯХ ДЕГРАДАЦИИ ВЫЧИСЛИТЕЛЬНОЙ СТРУКТУРЫ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10356 (дата обращения: 17.02.2026).



