При работе механизма загрузки порубочных остатков, перемещения его элементов происходят только в плоскости X-Z, поэтому разработана двумерная модель механизма. В общей модели (устройства для измельчения порубочных остатков, оснащенного механизмом загрузки) двумерная модель механизма загрузки добавляется к трехмерной модели устройства для измельчения порубочных остатков.
В настоящее время общепринятым методом моделирования сложных механизмов является матричный метод формирования общих уравнений из уравнений, описывающих отдельные элементы механизма [1,2,3,7]. Преимуществом данного метода является упрощенное и формализованное составление общей системы уравнений, недостатком метода – некоторая громоздкость системы дифференциальных уравнений и соответственно больший объем компьютерных вычислений [4,5].
В рамках данного метода механизм разбивается на несколько абсолютно твердых тел, взаимодействующих между собой несколькими связями определенных типов (шарнирное соединение, невесомая нерастяжимая тяга, связь с помощью гидроцилиндра и т.п.). При этом, в двумерном случае, положение каждого тела i в пространстве задается координатами центра тяжести (xi, zi) и углом наклона к горизонтальному направлению φi. Инерционные свойства тел задаются их массой mi и центральным моментом инерции Ji. Для каждого тела определяется набор точек (контактных точек), в которых это тело контактирует с любыми другими телами тем или иным способом [6].
Для каждого тела (рисунок 1) вводим систему отсчета xi, yi, начало которой совмещаем с центром тяжести. Тогда положение связанных осей относительно неподвижной системы координат x0, z0 будет задаваться набором xi0, zi0, ji0. В связанной системе координат контактные точки удобно задавать полярными координатами rij, jij, где индекс i соответствует номеру тела (i = 1, 2, ..., n), j - номеру контактной точки (j = 1, 2, ..., m).
Условимся также, что неподвижная система координат есть некоторая система, связанная с условным телом номер ноль (i = 0). Поэтому точки, принадлежащие неподвижной системе координат (некоторые жесткие заделки), будем задавать также полярными координатами вида r0i, j0i. Центр тяжести любого тела будем считать нулевой точкой (j = 0).
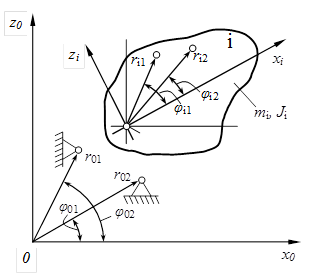
Рисунок 1 – Схема индексации контактных точек тела механизма в полярной системе координат
В соответствии с предложенными правилами индексации механизм загрузки был разбит на отдельные твердые тела и связи следующим образом (рисунок 2).
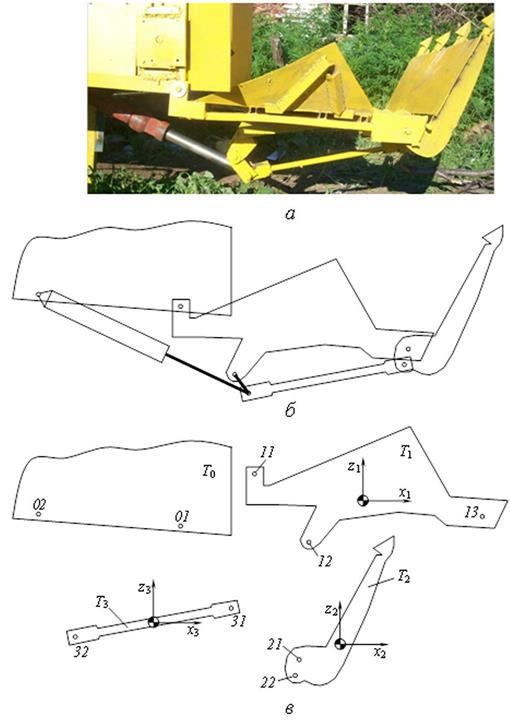
Рисунок 2 – Представление механизма загрузки в модели, как совокупности отдельных твердых тел и связей между ними: а – фотография механизма; б – взаимосвязь тел механизма; в – индексация тел и контактных точек механизма
Механизм разбит на три абсолютно твердых тела: T1 – стрела; T2 – захват; Т3 – нижняя тяга. Кроме того, в качестве неподвижного "нулевого" тела T0 рассматривается корпус устройства для измельчения порубочных остатков.
Тела механизма взаимодействуют тремя типами связей:
- цилиндрическими шарнирами (01–11, 13–21, 22–31);
- невесомой нерастяжимой тягой (12–31);
- гидроцилиндром (02–32).
Для записи уравнений движения механизма в целом используются уравнения Лагранжа I рода с неопределенными множителями в виде
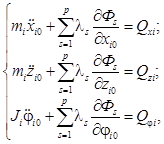 (1)
(1)
где Qxi, Qzi – декартовы составляющие равнодействующих сил, приложенных к i-му телу; Qφi – соответствующий момент; λs – неопределенные множители Лагранжа (s = 1, 2, ..., p); Фs – функции связей.
При составлении общей системы уравнений вначале последовательно рассмотрим три типа связей, присутствующие в данном механизме (рисунок 3), после чего "смонтируем" общую систему уравнений механизма, руководствуясь при этом определенными правилами последовательного индексирования уравнений.
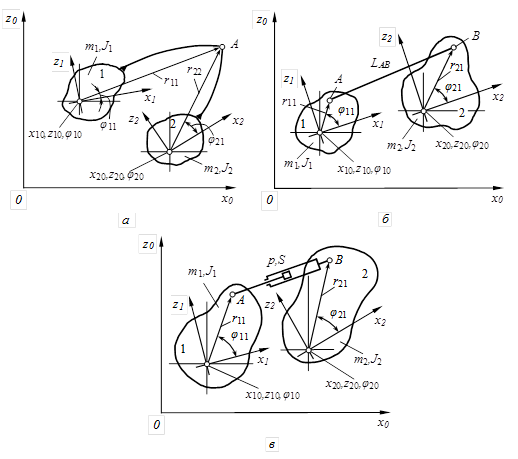
Рисунок 3 – Расчетные схемы для трех видов связей в моделируемом механизме: а – цилиндрический шарнир; б – нерастяжимая тяга; в – гидроцилиндр
При составлении уравнений движения для шарнирной связи и нерастяжимой тяги (рисунок 3, а и б) учитываем заложенные в данный вид связи ограничения (неразрывность, равенство углов поворота, неизменность заданного расстояния), записываем функции связей, затем определяем коэффициенты при множителях Лагранжа путем дифференцирования функций связи, после чего подставляем эти коэффициенты в уравнения (1), с учетом вторых производных функций связи по времени. Тогда, опуская промежуточные преобразования, получим для шарнирной связи искомую систему уравнений в матричной форме.
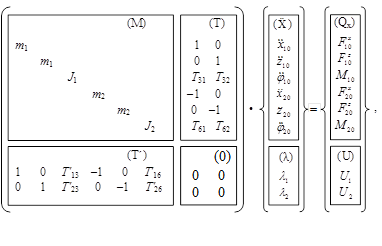 (2)
(2)
где Т´13 = Т31 = –r11sin(φ10+φ11); Т´16 = Т61 = r21sin(φ20+φ21);
Т´23 = Т32 = –r11cos(φ10+φ11); Т´26 = Т26 = –r21cos(φ20+φ21);
U1 = r11cos(φ10+φ11)![]() – r21cos(φ20+φ21)
– r21cos(φ20+φ21)![]() ;
;
U2 = r11sin(φ10+φ11)![]() – r21sin(φ20+φ21)
– r21sin(φ20+φ21)![]() ;
;
![]() ,
, ![]() и
и ![]() – проекции равнодействующей внешних сил, действующих на первое тело и суммарный момент этих сил относительно центра тяжести этого тела;
– проекции равнодействующей внешних сил, действующих на первое тело и суммарный момент этих сил относительно центра тяжести этого тела;
![]() ,
,![]() и
и ![]() – то же самое – для второго тела.
– то же самое – для второго тела.
Последнюю систему, как и системы для остальных рассматриваемых видов связей (рисунок 3), можно представить в виде обобщенного выражения
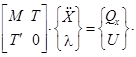 (3)
(3)
В выражениях (2) и (3) буквами обозначены следующие матрицы: М – диагональная подматрица масс, коэффициенты которой есть последовательные значения масс и моментов инерции; Т – прямоугольная подматрица коэффициентов при множителях Лагранжа размерности 6 ´ nλ, где nλ – число уравнений связи (коэффициенты матрицы вычисляются по специальным формулам); Т´– подматрица, транспонированная по отношению к матрице Т; 0 – нулевая подматрица; ![]() – подматрица линейных и угловых ускорений системы; λ – подматрица неопределенных множителей Лагранжа; Qx – подматрица внутренних и внешних возмущений, приведенных относительно центров тяжести тел; U – подматрица размерности n.
– подматрица линейных и угловых ускорений системы; λ – подматрица неопределенных множителей Лагранжа; Qx – подматрица внутренних и внешних возмущений, приведенных относительно центров тяжести тел; U – подматрица размерности n.
Формулы для частных случаев связи тела с неподвижной системой координат могут быть получены из системы вида (2) путем исключения всех координат, относящихся ко второму телу. В частности, для шарнирной связи тела 1 (стрелы) с телом 0 (корпусом устройства для измельчения порубочных остатков) получим следующую систему
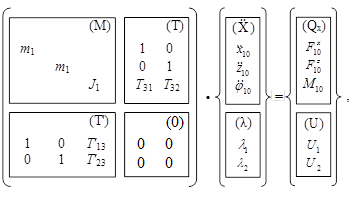 (4)
(4)
где Т´13 = Т31 = –r11sin(φ10+φ11); Т´23 = Т32 = –r11cos(φ10+φ11); U1 = r11cos(φ10+φ11)![]() ;
;
U2 = r11sin(φ10+φ11)![]() .
.
Системы уравнений, описывающие остальные виды связей, имеют такую же структуру, как и система (2). Отличие заключается в другом виде выражений для определения элементов подматриц, а также в размерностях самих подматриц, зависящих от числа nλ.
Для случая связи двух тел 1 и 2 (рисунок 3, б) с помощью невесомой нерастяжимой тяги (в точках А и В – цилиндрические шарниры) длиной LАВ nλ = 1, поэтому матрица Т имеет размерность 6 ´ 1, а вектор U состоит из одного элемента. Тогда, опуская промежуточные операции расчетов, запишем окончательно выражения для искомых элементов подматриц:
![]() , (5)
, (5)
![]() , (6)
, (6)
![]() , (7)
, (7)
![]() , (8)
, (8)
![]()
![]()
![]() . (9)
. (9)
В выражениях (5) ... (9) и в выражениях, составляемых ниже, с целью сокращения длины выражений условно приняты подстановки φ20 + φ21 = φ20* и φ10 + φ11 = φ10*, причем звездочки не проставлены.
Соединение двух тел с помощью гидроцилиндра (рисунок 3, в), для которого известны рабочая Sр, штоковая Sш, поршневая Sп площади, давление рг и коэффициент μТ сухого трения гидравлической пары, описывается следующими уравнениями:
![]() ; (10)
; (10)
![]() ; (11)
; (11)
![]() ; (12)
; (12)
![]() ; (13)
; (13)
![]() ; (14)
; (14)
![]() , (15)
, (15)
где ![]() ;
;
![]() ;
;
![]()
На основе приведенных выше систем уравнений для трех типов связей, составляется общая система уравнений, описывающая весь механизм. Для формирования общей системы необходимо иметь три вида исходных данных:
– о массах, моментах инерции и геометрии расположения контактных точек;
– о связях, объединяющих тела в механизм;
– о начальных условиях и прочие вспомогательные сведения, необходимые для осуществления процесса интегрирования.
Формирование общей системы уравнений на основании рассмотренных частных случаев осуществляется с помощью принципа суперпозиции: введение в систему каждой новой связи означает только введение соответствующих членов-столбцов в систему уравнений и никак не изменяет члены уравнений, отвечающие описанию всех других связей, реакций, сил. Это означает, что если выписать диагональную матрицу масс системы, то запись массива коэффициентов при множителях Лагранжа и массивов коэффициентов в правой части уравнения можно выполнить с помощью уравнений-шаблонов, выведенных ранее. При этом вид связи будет определять, каким именно шаблоном следует воспользоваться, а значения индексов контактных точек связи определят, какие значения rij и φij следует подставлять в формулы.
Рецензенты:
Маштаков Д.А., д.с.-х.н., доцент, заведующий кафедрой «Лесное хозяйство и лесомелиорация», ФГБОУ ВПО «Саратовский государственный аграрный университет им. Н.И. Вавилова», г. Саратов.
Панкратов В.М., д.т.н., профессор, заместитель директора, «Институт проблем точной механики и управления РАН», г. Саратов.
Библиографическая ссылка
Фетяев А.Н., Фокин С.В. О ПРЕДСТАВЛЕНИИ В МОДЕЛИ МЕХАНИЗМА ПОДЪЕМА ПОРУБОЧНЫХ ОСТАТКОВ ДИСКОВОЙ РУБИТЕЛЬНОЙ МАШИНЫ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10350 (дата обращения: 17.02.2026).



