Введение
Постоянное повышение надёжности машин и оборудования требует непрерывного совершенствования комплектующих, в том числе подшипников, следовательно, и деталей их составляющих, например роликов. Возрастают требования к геометрическим размерам роликов и качеству их поверхности. В связи с этим актуальной задачей считается обеспечение стабильности сферической поверхности торца ролика, во многом ответственного за надежность эксплуатационных параметров подшипника. Поэтому совершенствованию оборудования и технологии формообразования сферической поверхности на торце ролика уделяется большое внимание [3-5] и др.
Для образования сферической поверхности используется, в частности, специальный шлифовальный автомат мод. SXK-5A. Станок обрабатывает ролики с наружным диаметром 6 – 25 мм, углом конической поверхности 2 – 8°.
С помощью специального загрузочного устройства ролики ориентируют и подают к шпинделю изделия, где их устанавливают в сепаратор между двумя прижимными дисками. Прижимные диски и сепаратор расположены на одной оси. Диски имеют самостоятельные приводы, обеспечивающие их вращение в противоположных направлениях. Сепаратор вращается на валу свободно.
Перед входом в зону шлифования с помощью передней направляющей дуги ролики вдавливают между прижимными дисками, что обеспечивает их закрепление по конической поверхности. Относительно торцовой поверхности прижимного диска ролик должен выступать на заданную величину. По классификации, предложенной в работе [1], сферическую торцовую поверхность ролика подшипника можно отнести ко второй категории деталей, имеющих конструктивные элементы, препятствующие подводу инструмента.
Благодаря противоположному направлению вращения опорных дисков ролик приводится во вращение вокруг своей оси. В результате различной угловой скорости вращения опорных дисков ролик совершает дополнительное движение вдоль образующей шлифовального круга. Ролик перекатывается по конической поверхности опорного диска, вращающегося с меньшей угловой скоростью, в направлении вращения диска с большей угловой скоростью [2]. Свободно расположенный между опорными кольцами направляющий диск или сепаратор увлекается во вращение роликами. На сепараторе имеются выемки, в которых детали дополнительно ориентируются по своей конической образующей.
Особенности обработки на станке состоят в том, что ролик участвует одновременно в двух движениях: вращении ролика вокруг собственной геометрической оси; вращении ролика вместе с сепаратором вокруг оси опорных дисков (рис. 1). Примем, что в представленной схеме число оборотов второго диска больше первого: n2 > n1. Скорость вращения ролика вокруг собственной оси nр будет определяться наибольшей скоростью вращения прижимного диска n2=nmax, его радиусом R и радиусом ролика r, скорость вращения ролика, соответственно и сепаратора вокруг оси шпинделя nс – разностью скоростей n2–n1, R и r. Направление вращения сепаратора будет совпадать с направлением вращения второго диска (рис. 2).
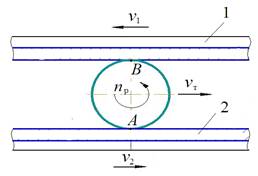
Рис. 1. Схема подачи ролика
Скорость вращения ролика вокруг собственной оси (об/мин) равна:
![]() , (1)
, (1)
где vr – скорость вращательного движения на радиусе r, м/мин.
Поскольку целью работы является определение скорости перемещения любой точки на торцовой поверхности ролика, vr найдем с учетом того, что торцовая поверхность ролика расположена на расстоянии h от периферии дисков, т.е. от R:
![]() , (2)
, (2)
где k2 – коэффициент проскальзывания между ведущим прижимным диском 2 и роликом.
Подставив (2) в (1), получим:
![]() . (3)
. (3)
Окружная скорость точки, лежащей на торцовой поверхности ролика и имеющей радиус ri, будет равна:
![]() . (4)
. (4)
Скорость вращения сепаратора nc (об/мин) найдем аналогично (2):
![]() , (5)
, (5)
где vт – скорость вращательного движения вокруг оси шпинделя торцовой поверхности ролика (м/мин).
Скорость vт найдём из условия качения ролика по диску 1 (рис. 1). В точке А скорость будет равна:
![]() ,
,
где k1 – коэффициент, учитывающий проскальзывание между диском 1 и роликом.
Тогда скорость движения центра ролика в этом относительном движении, равная 0,5vA, и будет определять скорость вращательного движения торцовой поверхности относительно оси шпинделя:
![]() . (6)
. (6)
Для всех точек торцовой поверхности ролика эту скорость можно считать одинаковой. Подставив (6) в (5), получим:
![]() . (7)
. (7)
Вектор скорости подачи для любой точки на торцовой поверхности ролика будет равен сумме вектора скорости точки во вращательном движении вокруг оси ролика и вектора скорости этой же точки во вращательном движении вокруг оси шпинделя:
![]() .
.
Рассмотрим изменение проекций скорости vr на оси координат (рис. 2). Модуль скорости точки во вращательном движении вокруг оси, согласно (4), будет определяться расстоянием от этой точки до оси вращения ri. Положение точки на плоскости зададим в полярной системе координат - определяется радиусом-вектором (расстоянием до полюса) r и углом α между полярной осью и радиусом-вектором. Полярный угол примем положительным при отсчёте от полярной оси против часовой стрелки. На рис. 2 показаны проекции vri на оси координат для точек, расположенных в различных четвертях окружности на максимальном расстоянии от центра вращения ролика.
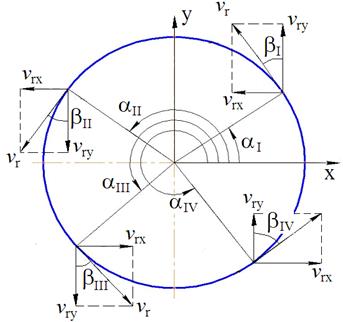
Рис. 2. Составляющие линейной скорости вращения ролика вокруг своей оси
Проекция окружной скорости vri на горизонтальную ось с учетом направления координатной оси равна:
в 1 и 2 четвертях окружности
vrхi= –vrisinβ; (8)
в 3 и 4 четвертях окружности
vrхi=vrisinβ. (9)
Для построения зависимости vrхi от угловой координаты произвольной точки на торцовой поверхности ролика рассмотрим связь между углами α и β в каждой четверти окружности (рис. 2):
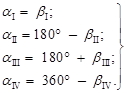 (10)
(10)
В соответствии с формулами приведения синуса из (10) получим следующие зависимости между синусами углов α и β:
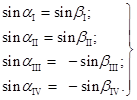 (11)
(11)
С учетом (11) зависимости (8) и (9) можно представить следующей обобщённой формулой:
vriх= – vrisinα. (12)
Подставив в (12) значение vri из (4), получим развёрнутое выражения для вычисления горизонтальной составляющей скорости подачи от вращения ролика вокруг собственной оси для любой точки на торце ролика:
![]() . (13)
. (13)
Аналогично найдем вертикальную составляющую vrхi. В каждой из рассмотренных четвертей окружности проекция vri на вертикальную ось (рис. 2) определяется формулой:
в 1 и 4 четвертях окружности
vryi= vricosβ; (14)
во 2 и 3 четвертях окружности
vryi= –vricosβ. (15)
В соответствии с формулами приведения косинуса из (9) получим следующие зависимости между косинусами углов α и β:
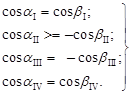 (16)
(16)
С учетом (16) зависимости (14) и (15) можно представить в следующем обобщённом виде:
vryi= vricosα. (17)
Подставив в (17) значение vri из (4), получим развернутое выражение для расчёта вертикальной составляющей скорости подачи от вращения ролика вокруг собственной оси для любой точки торцовой поверхности ролика:
![]() . (18)
. (18)
Вектор скорости вращательного движения ролика вокруг оси дисков в рассматриваемом случае совпадает с направлением горизонтальной оси координат. Тогда горизонтальная составляющая результирующей скорости подачи любой точки на поверхности ролика будет равна:
vsxi = vrxi + vт. (19)
Подставив в (19) значения слагаемых соответственно из (13) и (6), получим:
![]()
или
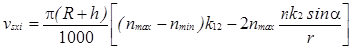 . (20)
. (20)
Модуль вектора скорости подачи для любой точки на торце ролика равен:
![]() . (21)
. (21)
Для вычисления модуля вектора скорости подачи в (21) необходимо подставить слагаемые соответственно из (20) и (18).
С использованием полученных формул рассчитаны скорости подач трех видов конических роликов, торцовые поверхности которых обрабатывают на станке SXK-5A на ОАО «ЕПК Волжский». В качестве примера на рис. 3 приведены результаты расчета по формуле (20) без учета коэффициента проскальзывания скоростей подач для различных точек торцовой поверхности ролика. Численное значение радиуса, на котором находятся выбранные точки, указано на графиках в мм. Окружные скорости вращения прижимных дисков при обработке роликов одинаковы и равны n1=26 об/мин; n2=30 об/мин. Исходные данные для расчета приведены в таблице 1. По внешнему виду полученные графические зависимости соответствуют функции синуса.
Представленные зависимости получены на полной торцовой поверхности без учета технологической выточки, имеющей определенный радиус r (табл. 1).
а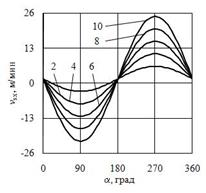 б
б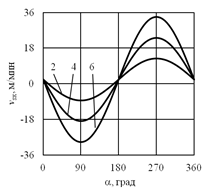 в
в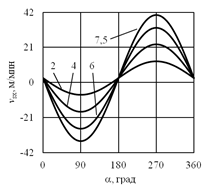
Рис. 3. Закономерности изменения горизонтальной составляющей результирующей скорости подачи роликов 1027313А (а), 7607А (б) и 7310А (в)
Таблица 1
Исходные данные для расчета скорости подачи
|
Обозначение ролика |
R, мм |
r, мм |
h, мм |
|
1027313А |
120,5 |
10,0 |
2,5 |
|
7607А |
170,5 |
6,2 |
2,5 |
|
7310А |
206 |
7,8 |
2,5 |
Для ролика 1027313А максимальная и минимальная составляющие результирующей скорости подачи равны соответственно 16 и 25 м/мин (рис. 3а), т.е. за оборот ролика вокруг своей оси скорость изменяется на 36%. На ролике 7607А (рис. 3б) составляющая результирующей скорости подачи изменяется от 24 до 35 м/мин, или на 31%; на ролике 7310А (рис. 3в) – от 26 до 41 м/мин, что составляет около 34%. Различие, например, в максимальных скоростях подачи между рассмотренными роликами составляет более 60%, что свидетельствует о необходимости совершенствования режима обработки.
Выводы
Получены формулы для расчета скорости подачи для любой точки базовой торцовой поверхности роликов конических подшипников на операции сферошлифования на станке SXK-5A, когда заготовка устанавливается в сепараторе, не имеющем специального привода, и зажимается двумя дисками, вращающимися в различные стороны от отдельных приводов. В результате ролик совершает вращение вокруг собственной оси и вращение в сепараторе вокруг оси шпинделя изделия.
Анализ действующего технологического процесса, выполненный с использованием разработанных моделей скорости подачи, показал, что при прочих равных или близких значениях остальных параметров скорость подачи может отличаться более чем на 60%, что свидетельствует о возможностях дальнейшего совершенствования процесса.
Рецензенты:
Кристаль М.Г., д.т.н., профессор кафедры «Автоматизация производственных процессов» ФГБОУ ВПО «ВолгГТУ», г. Волгоград.
Гольцов А.С., д.т.н., профессор, заведующий кафедрой «Автоматика, электроника и вычислительная техника» ВПИ (филиал) ФГБОУ ВПО «ВолгГТУ», г. Волжский.
Библиографическая ссылка
Носенко В.А., Зуев А.В., Морозов А.В. РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ПОДАЧИ РОЛИКА ПОДШИПНИКА НА СФЕРОШЛИФОВАЛЬНОМ СТАНКЕ SXK-5A // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10245 (дата обращения: 17.02.2026).



