Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Рассадникова Е.Ю. 1 Коханчиков Л.А. 2

---

1 Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Уфимский государственный авиационный технический университет»

2 ОАО «АНК»

Анализ работ мировых и российских ученых в области задач маршрутизации с «временными окнами» позволил сделать вывод, что их значительная часть посвящена задачам маршрутизации транспорта с учетом реальных ограничений. Авторами предложена модификация математической модели задачи выбора рациональных маршрутов в системе управления доставкой готовой продукции. Подбор маршрутов для обеспечения поддержки управленческих решений при транспортировке готовой продукции осуществляется с учетом минимизации совокупных затрат на транспортировку и дополнительных ограничений, таких как, приемлемые затраты на маршруты по платным дорогам, удовлетворительное качество дорог, приемлемый риск ДТП на дорогах и возможный ущерб от ДТП на маршрутах. Предлагается использование модифицированного алгоритма поиска переменной окрестности для решения задачи.

Статья в формате PDF

207 KB

задача маршрутизации транспортных средств.

задачи транспортной логистики

модели дискретной оптимизации

система управления транспортировкой

1. Юсупова Н.И., Валеева А.Ф., Рассадникова Е.Ю., Латыпов И.М., Кощеев И.С. Многокритериальная задача доставки грузов различным потребителям //Логистика и управление цепями поставок.2011. №6.С. 60-82

2. Bettinelli A., CeselliA., RighiniG. A branch-and-cut-and-price algorithm for the multi-depot heterogeneous vehicle routing problem with time windows// Original Research Article, Transportation Research Part C: Emerging Technologies. 2011. Volume 19. Issue 5. P. 723-740

3. Dondo R., Cerdá J. A cluster-based optimization approach for the multi-depot heterogeneous fleet vehicle routing problem with time windows // European Journal of Operational Research. 2007. Volume 176. Issue 3. P. 1478-1507

4. Leonelli P., Bonvicini S., Spadoni G. Hazardous materials transportation: a risk-analysis-based routing methodology//Journal of Hazardous Materials. 2000. Volume 71. Issues 1–3. P. 283-300

5. Reza Z.F., Rezapour Sh., Kardar L. Logistics Operations and Management, Concepts and Models // Elsevier Inc. 2011.P. 469

6. Zografos K.G., Androutsopoulos K.N.A heuristic algorithm for solving hazardous materials distribution problems // European Journal of Operational Research. 2004. Volume 152. Issue 2. P. 507-519

7. Zografos K.G., Androutsopoulos K.N. A decision support system for integrated hazardous materials routing and emergency response decisions//Transportation Research Part C: Emerging Technologies. 2008.Volume 16. Issue 6.P. 684-703

Введение

В настоящее время перед компаниями, занимающимися производством продукции и ее доставкой клиентам, встает вопрос о повышении эффективности управления системой транспортировки. С этой целью компании используют так называемые системы управления транспортом (TransportationManagementSystem (TMS)). Применение TMS позволяет компаниям за счет обеспечения поддержки управленческих решений сократить временные простои используемых для перевозки транспортных средств (ТС) и снизить их количество, обеспечив тем самым, снижение стоимостных затрат на транспортировку. Функциональными возможностями систем управления транспортировкой являются планирование и подготовка принятия решений (по оптимизации маршрутов транспортных средств, входящему и исходящему режиму транспортировочных операций и др.), мониторинг, анализ, составление отчетности.

Тот или иной набор функциональных возможностей систем управления транспортом позволяет условно разделить их на два типа. Для первого типа TMS (например, пакеты прикладных программ ArcLogistics (Esri, Inc, 1998), DescartesRouting, Mobile&TelematicsSuite (DescartesSystemsGroup, 1998), DISC (MJC2, 1990), IBM ILOG TransportationAnalyst (IBM, 2000); а также ANTOR LogisticsMaster (ANTOR Бизнес Решения, 2003), TopLogistic (TopPlan)) характерны функции планирования, анализа и управления, составления отчетности. Системы второго типа (например, пакеты прикладных программ ГлонассOmnicomm (Omnicomm,1998), ANTOR МonitorMaster (Информационные технологии, 2003)) связаны с мониторингом деятельности компании в реальном масштабе времени.

Важное место в TMS занимают функции планирования и оптимизации маршрутов транспортных средств. В приведенных выше примерах пакетов прикладных программ для нахождения рационального маршрута доставки грузов чаще всего решается задача маршрутизации транспортных средств с временными окнами (VRPTW) с учетом дополнительных ограничений. В статье предлагается оптимизировать маршруты доставки продукции на основе модели MultiDepotHeterogeneous VRP withTimeWindows (MDHVRPTW) [3] с учетом дополнительных ограничений, таких как риск ДТП, возможный ущерб компании от аварии во время транспортировки грузов, качество дорог.

Задача решается для производственных предприятий, имеющих широкую номенклатуру выпускаемой продукции и расположенные в различных городах структурные подразделения. Доставка продукции осуществляется потребителям в отдаленные города. Примером такого предприятия может служить нефтехимическое, производящее реагент, который используется для защиты трубопроводов от коррозии, а также в качестве исходного сырья для производства присадок к маслам и смазочно-охлаждающим жидкостям.

Постановка задачи транспортировки готовой продукции

Для транспортировки нескольких видов готовой продукции (ГП), производимых в разных городах используются ТС различного типа, которые размещаются в нескольких депо-производственных пунктах. Основными требованиями при транспортировке продукции считаются снижение затрат, удовлетворение всех потребителей готовой продукции с учетом предпочтительного времени обслуживания и возвращение транспортных средств в депо в установленный период, обеспечение безопасности доставляемой ГП. Для обеспечения безопасности транспортировки ГП дополнительно необходимо учитывать такие требования, как приемлемый риск дорожно-транспортных происшествий (ДТП), возможный ущерб от ДТП и др.

Для обеспечения поддержки решений при управлении транспортировкой готовой продукции необходимо осуществить выбор набора маршрутов, что сводится к задаче маршрутизации транспорта (VehicleRoutingProblems, VRP). Целью подбора маршрутов транспортировки ГП является минимизация общих стоимостных и временных затрат.

Анализ работ мировых и российских ученых в области задач маршрутизации с «временными окнами» позволил сделать вывод, что их значительная часть посвящена задачам маршрутизации транспорта с учетом реальных ограничений (таблица 1)[5].

Таблица 1 – Обзор моделей VRP with TW

Для формализации описанной задачи используется математическая модель MultiDepotHeterogeneous VRP withTimeWindows (MDHVRPTW)[3]. Авторами предлагается модификация математической модели MDHVRPTW для выбора маршрутов с учетом введения условий и ограничений:

• доставка заказа может быть разделена между ТС, то есть клиент может быть обслужен несколькими ТС;
• осуществляется доставка нескольких видов ГП;
• грузоподъемность ТС не должна быть превышена;
• ТС может быть назначено не больше, чем на одно депо;
• обслуженные заказы ТС не должны превышать вместимость депо;
• каждый клиент должен быть полностью удовлетворен − это означает, что каждый клиент должен быть обслужен хотя бы один раз;
• выбранный период возвращения ТС в депо должен быть выполнен, если этот период не выполняется, планируемые затраты увеличиваются;
• «временные окна» для каждого клиента должны быть выполнены, если эти «окна» не выполняются, планируемые затраты увеличиваются;
• выбранные маршруты должны проходить по качественным дорогам;
• плата за используемые дороги на выбранном маршруте не должна быть выше, чем допустимая величина;
• выбранный маршрут не должен превышать допустимый риск ДТП.

Специальные обозначения и определения

Для решения задачи выбора маршрута используются следующие обозначения и определения, принятые в разрабатываемой модели.

Множества:

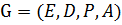• – взвешенный граф, где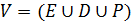– все вершины в этом графе;
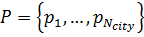• – множество вершин-городов, через которые транспортные средства могут проходить, 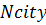– количество сквозных городов;
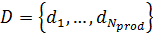• – множество вершин городов депо-производственных пунктов, где реагент производится, 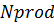– количество депо-производственных пунктов;
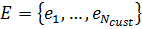• – множество городов-клиентов, где 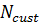– количество городов-клиентов; 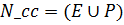– объединение множества 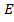и ;
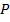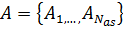• – множество ребер (дорог) графа, 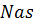– количество ребер.
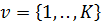• – множество транспортных средств с грузоподъемностью 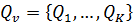, размещенных в депо-производственных пунктах 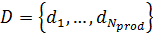; 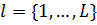– несколько типов товаров, произведенных предприятием.

Параметры:

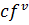• – фиксируемая стоимость использования ТС ;
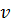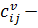• стоимость, зависимая от пройденной дистанции между двумя точками для ТС ;
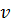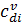• – стоимость, зависимая от пройденной дистанции между депо и клиентом для ТС ;
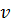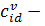• стоимость, зависимая от пройденной дистанции между клиентом и депо для ТС ;
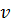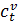• – стоимость пройденного времени в единицу времени;
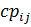• – стоимость «платности» для ребра;
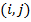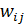• – вес для каждого ребра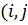) (введен для учета качества дорог);
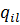• – спрос каждого города-клиента 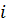для продукта ;
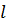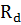• – вместимость депо;
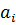• – раннее возможное время обслуживание вершины ;
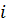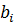• – позднее время обслуживания вершины ;
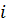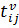• – время в пути между вершинам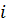и и ;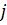
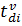• – время в пути между депо 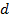и вершиной ;
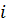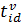• – время пути между вершиной 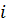и депо ;
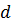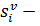• время обслуживания вершины .

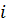Вершины «депо» и «сквозные» города не имеют спроса и сервисного времени, т.е. ; ∀.

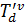• – время отправления транспортного средства 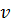из депо;
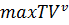• – максимальное время окончания работы для транспортного средства ;
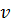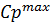• – максимально допустимая оплата за платные дороги;
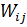• – минимально возможный уровень качества дорог «ребер»;
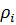• – штрафная стоимость при нарушении временного окна вершины (клиента) ;
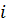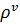• – штрафная стоимость для нарушения максимального времени работы для ТС ;
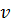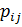• – вероятность ДТП на дороге (ребре);
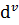• – ущерб компании от ДТП;
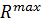• – допустимый риск.

Логические переменные:

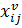• – принимает значение 1, если ТС 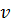движется в направлении от вершины 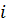к вершине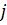, и 0 – при движении в обратном направлении, и обозначает, что вершина i посещается до или после вершины j;
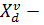• обозначает назначение ТС 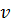к депо ;
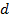• обозначает назначение ТС, 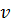к вершине .

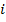Переменные:

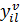• – спрос i-ого клиента, удовлетворенный ТС ;
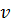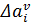• – нарушение начала времени обслуживания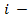го клиента;
• Δ 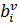– нарушение окончания времени обслуживания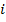- ого клиента;
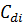• - стоимость пройденного расстояния от депо 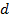to к вершине ;
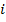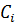• - стоимость пройденного расстояния до вершины ;
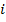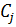• – стоимость пройденного расстояния до вершины ;
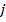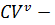• стоимость пройденного расстояния ТС ;
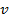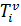• – время прибытия ТС к клиенту (в вершину) ;
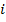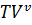• - время возвращения ТС ;
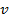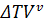• – нарушение времени возвращения ТС ;
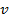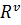• – риск ДТП на маршруте для ТС .

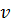Приведенные обозначения используются далее для описания математической модели.

Математическая модель для задачи выбора рациональных маршрутов

Выбор рационального маршрута основывается на минимизации общих сервисных затрат (1), которые включают в себя фиксированную стоимость использования ТС ; стоимость, зависимую от пройденного расстояния и времени в пути ; стоимость времени ожидания и сервисного обслуживания; штрафные величины - и ; величину риска в маршруте .

(1)

При решении задачи выбора рациональных маршрутов, направленной на минимизацию общих сервисных затрат, необходимо учитывать следующие ограничения:

1. Маршруты ТС не могу заканчиваться в городах-клиентах и «сквозных» городах:

, где

– посещенная вершина.

2. Каждое, использованное ТС должно быть размещено в одном депо, в которое ТС будет возвращаться после посещения всех назначенных для него клиентов:

, .

3. Каждый клиент может быть посещен несколькими транспортными средствами:

, .

4. Удовлетворенный спрос клиента ТС должен быть не больше спроса на продукт клиента :

, .

5. Спрос каждого клиента должен быть удовлетворен полностью:

,

6. Количество доставляемого товара ТС не должно превышать его грузоподъемность:

, , .

7. Стоимость пройденного расстояния до вершины из депо для ТС :

, ,

.

8. Стоимость пройденного расстояния между на одном маршруте

.

9. Общая стоимость пройденного расстояния ТС .

.

10. Время прибытия в вершину

.

11. Начала времени обслуживания в паре вершинна одном маршруте

.

12. Время окончания маршрута ТС

,

.

13. Время отправления из вершины

.

14. Штрафные величины из-за нарушений времени обслуживания клиентов:

15. Штрафная величина из-за нарушений времени возвращения ТС

16. Сумма спроса клиентов не может превышать вместимость обслуживающего депо:

,

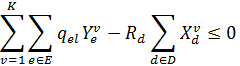
17. Для учета качества дорог использована классификация дорог согласно постановлению от 28 сентября 2009 г. № 767 «Правила классификации автомобильных дорог в Российской Федерации и их отнесения к категориям автомобильных дорог»:

M – для автодорог федерального значения, соединяющих Москву со столицами иностранных государств и административными центрами субъектов РФ;

Р – для автодорог федерального или регионального значения, соединяющих административные центры РФ;

А – для автодорог федерального или регионального значения, являющихся подъездом к крупнейшим транспортным узлам (например, аэропортам), подъездом к специальным объектам, либо подъездом от административного центра субъекта РФ, не имеющего дорожной связи с Москвой, к морским или речным портам, аэропортам и железнодорожным станциям либо границам других государств. Также применяется для автодорог, соединяющих дороги федерального значения между собой.

К – для прочих автодорог регионального значения.

Н – для автодорог межмуниципального значения.

Выбранные маршруты могут включать в себя дороги типов А, P, M.

*

Для всех ;

},

18. Плата за используемые дороги на выбранном маршруте не должна быть выше, чем максимально допустимая оплата за платные дороги:

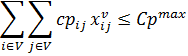
19. Найденный риск ДТП маршруте должен быть не больше допустимой величины риска:

Для нахождения величины риска ДТП на дороге (ребрах) примем два допущения:

• ущерб от ДТП на любом интервале маршрута одинаков;
• если ДТП случается, маршрут все равно продолжается.

Определение вероятности ДТП зависит от типа дорог в соответствии с нормативным документом «Автомобильные дороги и мосты. Влияние развития и состояния дорожной сети на уровень безопасности движения на дорогах России» от 2003 г., Москва, то есть – вероятность ДТП (величина на 100 км) на участке дорог. Значит , , , , .

,

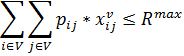
20. Ущерб компании от ДТП на выбранном маршруте определяется следующим образом:

– ущерб компании от ДТП включает в себя ущерб водителя (ущерб от смерти водителя); - ущерб транспортного средства; - ущерб потери партии товара, т.е. =.

Ограничения математической модели были проверены на работоспособность в программном продукте Xpress IVE.

Методы решения задачи

Поставленная задача является NP-трудной проблемой. Алгоритмы для решения таких задач должны быть эффективными, простыми и способными получать решение за минимальное время.

В настоящее время для решения задач маршрутизации с временными окнами, наибольший интерес вызывают следующие алгоритмы: поиск с исключениями (M.Gendreau, A. Hertz, G. Laporte, I. H. Osman и др.), генетический алгоритм (J. L. Blanton, G. Jeon и др.), алгоритм на основе муравьиных колоний (B. Bullnheimer и др.) и нейронные сети (Y. Matsuyama и др.), моделируемый и детерминированный отжиг (I. H. Osman и др.), поиск переменной окрестности (Mladenović, Hansen, и др.).

Для решения поставленной задачи используется алгоритм модифицированного поиска переменной окрестности. В настоящее время эффективность предложенного алгоритмического обеспечения проверяется посредством опытной эксплуатации программного продукта «Optimizationofgoodstransportation».

Заключение

Результаты анализа особенностей деятельности транспортных служб нефтехимического предприятия позволили сделать вывод о возможности использования математической модели MDHVRPTW с учетом введения дополнительных ограничений, таких как, приемлемые затраты на маршруты по платным дорогам, удовлетворительное качество дорог, приемлемый риск ДТП на дорогах и возможный ущерб от ДТП на маршрутах.

Для поддержки принятия решенияв системе управления транспортировкой ГП осуществляется выбор набора маршрутов на основе алгоритма поиска переменной окрестности, так как данный метод позволяет получить хорошие решения за приемлемое время в задачах большой размерности.

Работа частично поддержана грантами РФФИ 11-07-00579-а (Интеллектуальная система принятия решений в задачах оптимизации раскроя и упаковки на основе многоагентного подхода) и 12-07-00631-а (Информационные системы, нацеленные на решение практических задач упаковки многомерных ортогональных многогранников) и выполнены в рамках научно-исследовательской работы по теме 8.1224.2011.Результаты работы были получены во время стажировки в Рурском университете Бохума на кафедре Исследования операций, финансируемой международной программой ErasmusMundusMultic.

Рецензенты:

Сметанина О.Н., д.т.н., профессор кафедрой вычислительной математики и кибернетики, ФГБОУ ВПО Уфимского государственного авиационного технического университета, г.Уфа.

Юсупова Н.И., д.т.н., профессор, зав. кафедрой вычислительной математики и кибернетики, декан факультета информатики и робототехники, ФГБОУ ВПО Уфимского государственного авиационного технического университета, г.Уфа.

Библиографическая ссылка