Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Хаймович А.И. 1

---

1 ФГБОУ ВПО «Самарский государственный аэрокосмический университет им. акад. С. П. Королева (Национальный исследовательский университет)»

Излагается вывод системы уравнений движения деформируемой среды с учетом её зернограничной структуры. Определен способ расчета теплового и напряженно-деформированного состояния, исходя из полевых уравнений движения среды. Данные уравнения могут быть использованы для анализа влияния напряженно-деформированного состояния на динамику изменения микроструктуры в технологических процессах с интенсивной деформацией. В форме дифференциальных уравнений были получены аналитические зависимости, устанавливающие связь между 32 параметрами, характеризующими состояние деформируемой поликристаллической среды. Среда представлена как гетерогенная структура, состоящая из двух термодинамически взаимодействующих, непрерывной и носящей дискретный характер, зернограничной компонент.

Статья в формате PDF

806 KB

пластичность.

гетерогенная среда

интенсивная деформация

напряженно-деформированное состояние

поликристаллическое тело

1. Ильюшин А. А. Пластичность. Основы общей математической теории. [Текст] / А. А. Ильюшин. – М.: Изд-во. АН СССР, 1963. – 271 с.

2. Хаймович А. И., Михеев В. А. Математическое моделирование процессов динамической рекристаллизации поликристаллических материалов в условиях интенсивной пластической деформации [Текст] / А. И. Хаймович, В. А. Михеев // Кузнечно-штамповочное производство. – М., 2011. – № 7. – C.37-44.

3. Шитарев И. Л., Хаймович А. И. [Текст] / Методы повышения ресурса компрессорных лопаток из титановых сплавов при их высокоскоростной штамповке (ВСШ) с нагревом заготовок выше точки полиморфных превращений / И. Л. Шитарев, А. И. Хаймович // Вестник СГАУ им. акад. С. П. Королева. – Самара, 2012. – №3 (34), часть 4.- С. 34 – 40.

4. Шитарев И. Л., Хаймович А. И. Моделирование микроструктуры при высокоскоростной штамповке лопаток из титанового сплава ВТ9 [Текст] / И. Л. Шитарев, А. И. Хаймович // Заготовительные производства в машиностроении. – М.: Машиностроение, 2011. – № 11. – С.41-44.

5. Thomas J. P. Mesoscale modeling of the recrystallization of waspaloy and application to the simulation of ingot-cogging process (reprint) [Электронный ресурс] / Jean-Philippe Thomas, S. L. Semiatin/ URL: http://www.dtic.mil/cg bin/GetTRDoc?AD=ADA463582

В технологических процессах пластического формообразования современных поликристаллических сплавов для получения структуры штампованной заготовки, обеспечивающей требуемые механические свойства, необходимы большие интенсивные деформации [3,4]. При проектировании таких технологических процессов требуется учет гетерогенности свойств деформированного материала, что является следствием его поликристаллической структуры. Классическая математическая теория пластичности рассматривает деформируемые тела как гомогенную среду [1]. Современные инженерные подходы, которые позволяют моделировать поликристаллический характер среды, например, явление динамической рекристаллизации, в зависимости от напряженно-деформированного состояния (прямая задача) используют эмпирический или полуэмпирические подходы [2,5]. Настоящая работа ставит своей целью изложить основные уравнения пластически деформируемой поликристаллической среды, которые позволяют решить как прямую, так и обратную задачу – определить аналитически, каким образом имеющееся текущее состояние микроструктуры деформируемой среды влияет на НДС и последующие состояния микроструктуры.

Физическая модель деформируемого поликристаллического объекта представляет собой изотропную по фазовому составу среду в виде локальных конечных объемов (зерен), разделенных границами. Процесс пластического формоизменения зёрен и их границ моделируется как течение 2-х компонентной гетерогенной среды с активным взаимодействием 2-х структур – континуальной (зерна) и дискретной (граница зерна). В этой связи уравнения движения среды должны учитывать термомеханическое взаимодействия 2-х структур – зерна и границы зерна в процессе деформирования. Последнее требование обуславливает применяемые в исследовании подходы при моделировании:

• Анализ функций состояния деформируемой среды, которые определяются с помощью термодинамики необратимых процессов и связывают напряжения и скорости деформации.
• Переход от континуальной среды зерна к его дискретной границе с помощью введения операций дискретизации.
• Уравнения связи между кинематическими параметрами течения и параметрами микроструктуры.

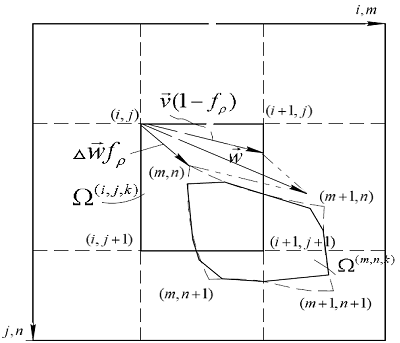
Рисунок 1. Поле скоростей материальной частицы и положение узлов координатных сеток (i,j,k) и (m,n,p) в момент времени t+δt.

Обозначим i, j, k – индексы узлов координатной сетки (i,j,k), охватывающей зерно в момент времени , m, n, p – индексы узлов второй сетки (m,n,p), перемещаемой вместе с границами зерна.

Для любой материальной точки, лежащей на границе зерна, применим принцип аддитивности пластического течения, согласно которому скорость массопереноса поликристаллической структуры происходит как суперпозиция поля скорости массопереноса локального объема внутри зерна и поля скорости миграции границы зерна, которое вызывает изменение его формы и размеров (рис. 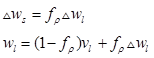1).

, (1)

где коэффициент структурообразования для каждой точки среды с координатами определяет, какой удельный объем в этой точке перемещается подобно континуальной составляющей, а какой мигрирует вместе с границами зерна. Если миграция (перемещение) границ зерна отсутствует, то (как в центре зерна), соответственно на границе зерна стремится к некоторому максимальному значению . Для того чтобы сохранить локальную непрерывную топологию среды как континуума, введем параметр дискретизации такой, что – в точке на границе зерен, – в точках внутри зерен. В этом случае:

,

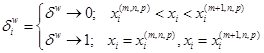(2)

Очевидно, что является статистической величиной.

Принимая во внимание принятые обозначения, условием динамического равновесия системы континуальная среда – зернограничная структура запишутся в форме (3).

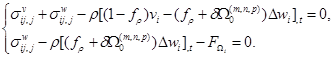, (3)

где и – соответственно компоненты тензоров напряжений, относящихся к континуальной и зернограничной составляющим деформируемой среды;

– изменение локального объема, вызванного миграцией границы зерна;

– сила взаимодействия между 2-мя составляющими деформируемой среды;

– плотность деформируемой среды (принята инвариантной). Здесь и далее в нижнем индексе при переменных принято обозначение оператора 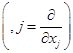, так что для компонентов тензора в пространстве с учетом соглашения Эйнштейна для повторяющихся индексов обозначается: .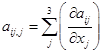

Неизвестную величину взаимодействия в (3) определим, пользуясь методами термодинамики необратимых процессов. Общая энтропия S в объеме среды распадается на энтропию , изменяемую окружением через поверхность , ограничивающую рассматриваемый объем, и необратимо возрастающую энтропию Si. По неравенству Клаузиуса – Дьюхема:

, (4)

Неравенство (4), преобразованное к локальной форме, приводит к неравенству:

. (5)

Дифференцируя второй член в (5), приходим к соотношению:

(6)

Множитель в (6) представляет собой дифференциальное уравнение теплопередачи, которое мы определим из первого закона термодинамики.

Опуская вывод уравнения баланса энергии, приведем первое начало термодинамики для локального объема, решая его относительно внутренней энергии :

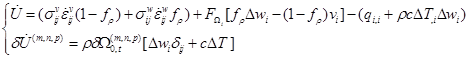(7)

- символ Кронекера.

Из (7) видно, что изменение внутренней энергии вызывается работой, производимой внешними силами (слагаемое в первых скобках), внутренним трением, вызванным перемещением границ зерен (второе слагаемое), а также теплом, проводимым и передаваемым (последнее слагаемое). Второе уравнение в (7) связано с изменением внутренней энергии , вызванным переносом тепла при миграции границ зерен и изменением массы, локализованной у границы зерна.

Из (6) и (7) следует:

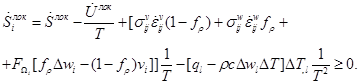(8)

Второе слагаемое в (8) определим через свободную энергию Гельмгольца: , которую представим в виде функционала , такого, что существует линейная комбинация . В этом случае изменение свободной энергии F будет равно

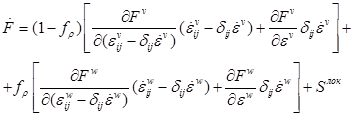, (9)

где – компоненты девиатора скорости деформации, .

С учетом (9) неравенство (8) примет вид:

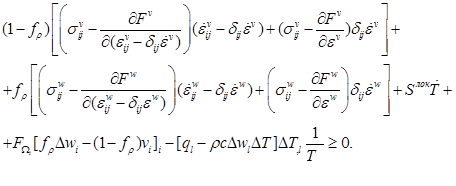(10)

Поскольку, как следует из (10), справедливы определяющие соотношения

и неравенство влечет за собой выполнение закона теплопередачи (11)

то зависимость (10) выполняется тождественно, если выполняется

, (12)

где – функция диссипации мощности, связанная с затратой энергии на структурообразование, вызванное относительным (по полю скоростей ) движением границ зерен.

Учитывая выполнение неравенства (12), можно записать разложение в ряд: , откуда, принимая во внимание первый член ряда при n=1, имеем:

(13)

где – коэффициент, учитывающий сопротивление внутреннему трению, будет определен далее из обобщенного уравнения теплопередачи.

Свободная энергия F есть скалярная величина инварианта состояния скоростей деформации и температуры. В общем случае: , в частном:

(14)

где инварианты:

Раскладываем в ряд Тэйлора в окрестности естественного состояния по отношению к кинетическим переменным и времени деформирования t, пренебрегая членами выше второго порядка для кинетических переменных и членами выше первого порядка для времени t:

(15)

Определим , (16)

где , – коэффициенты свойств материала.

Первое слагаемое в (16) зависит от параметров течения среды в области, локализованной у границы зерен, второе слагаемое определяет степень влияния континуальной компоненты на зернограничную составляющую, а третье – характеризует вязкотекучесть приграничного слоя.

Определив значения частных производных от F в (15) в точке как характеристики свойств материала и произведя действия над (15) и (16), аналогичные действиям (8) – (11), получим определяющие соотношения для деформируемой поликристаллической среды.

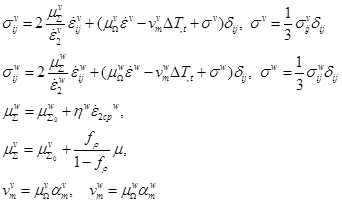, (17)

где – интенсивности скоростей деформаций для континуальной и зернограничной компонент, , ;

, – модули сдвига для континуальной и зернограничной компонент ;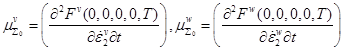

, – модули объемной деформации для соответствующих компонент среды;

– инвариант, соответствующий средней за процесс деформирования интенсивности скорости деформации;

– коэффициенты теплового расширения и тепловой миграции границ зерна.

Для определения коэффициентов из (17), характеризующих теплофизические свойствами компонентов деформируемой среды, введем функцию Гиббса G, выраженную через работу деформирования:

(18)

Определим G в терминах напряжений, для чего подставим определяющие соотношения (17) в (18), откуда получаем:

(19)

Выразим изобарную теплоемкость через энергию Гиббса G:

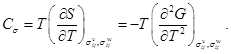(20)

Произведя дифференцирование (20) с учетом значения для G в форме (19), получаем различия в специфическом тепле при постоянном давлении и объеме :

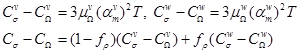(21)

Откуда имеем:

(22)

Из зависимости для материальной производной внутренней энергии следует , что совместно с (22) и законом теплопередачи (11) приводит к выводу обобщенного уравнения для передачи тепла в поликристаллической среде:

(23)

Рассмотрев (23) в стационарных условиях изотермической выдержки на границе зерна, получаем оценку для коэффициента из закона движения для поликристаллической среды в форме (13):

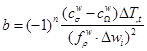, (24)

где определяет направление процесса динамической рекристаллизации ().

Принимая во внимание (24) и учитывая тот факт, что основной объем деформируемой сплошной среды приходится на континуальную составляющую и коэффициент структурообразования носит дискретный характер, уравнение теплопередачи равносильно системе

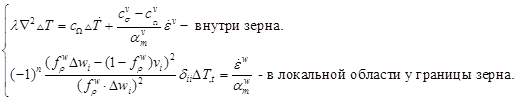, (25)

Коэффициент тепловой миграции границы зерна найдем, используя феноменологический подход, предполагая, что размер зерна пропорционален функции, описывающей диффузию.

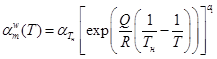, (26)

где – энергия активации самодиффузии, – универсальная газовая постоянная, , – постоянные коэффициенты.

В итоге мы имеем 32 параметра, характеризующие состояние деформируемой поликристаллической среды в локальной области:

• 3 компонента скорости перемещения среды ;
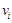• 3 компонента скорости миграции границ зерен ;
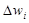• 6 компонент тензора деформации сплошной среды ;
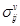• 6 компонент тензора напряжений 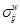в области, локализованной у границы зерна;
• Параметр структурообразования ;
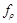• Приращение температуры 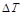в процессе деформирования;
• Коэффициенты 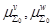, входящие в модули сдвига для основного материала и материала локализованного у границы зерна;
• Коэффициенты 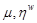, характеризующие реологические свойства материала локализованного у границы зерна;
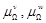• - модули объемной деформации основного материала и материала локализованного у границы зерна;
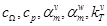• – соответственно удельные изохорные и изобарные теплоемкости, коэффициенты теплового расширения, коэффициент преобразования энергии пластической деформации в тепловую;
• Закон изменения плотности .

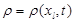Указанным 32 параметрам соответствуют 32 уравнения движения деформируемой поликристаллической среды, которые их связывают в единую модель:

• 2 уравнения непрерывности
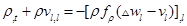  , для несжимаемой среды ,
  ;
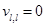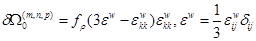• 6 уравнений движения (равновесия) в форме (3) с входящим в них законом движения (13) и (24);
• 14 физических соотношений связи между напряжениями и скоростями деформаций в форме (17);
• 2 соотношения связи между изобарной и изохорной теплоемкостями (21) с учетом 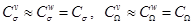и одна зависимость (26) для коэффициента тепловой миграции границы зерна ;
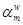• уравнение теплопередачи в виде (23) или (25);
• известные справочные или экспериментально полученные значения констант и коэффициентов , ;
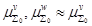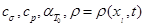• уравнение преобразования энергии пластической деформации в тепловую .

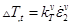В результате в форме дифференциальных уравнений получены аналитические зависимости, устанавливающие связь между 32 параметрами, характеризующими состояние деформируемой поликристаллической среды. Среда представлена как гетерогенная структура, состоящая из двух термодинамически взаимодействующих, непрерывной и носящей дискретный характер, зернограничной компонент.

Рецензенты:

Проничев Н. Д., д.т.н., профессор кафедры «Производство двигателей летательных аппаратов», Самарский государственный аэрокосмический университет им. акад. С. П. Королева (Национальный исследовательский университет), г. Самара.

Попов И. П., д.т.н., профессор кафедры «Обработка металлов давлением», Самарский государственный аэрокосмический университет им. акад. С. П. Королева (Национальный исследовательский университет), г. Самара.

Библиографическая ссылка