Введение
Под параметрическим описанием рисунка будем понимать такое, которое включает перечень свойств и их количественных характеристик. Запись результата такого описания можно назвать первым шагом в кодировании рисунков. С 2001 г. на «Материалы и изделия облицовочные из горных пород» действует ГОСТ 30629-99, принятый в 7 странах, который регулирует группу важнейших требований к декоративному камню. Согласно ему «Рисунок горной породы – совокупная характеристика, оцениваемая сочетанием и числом цветов, характером структуры и текстуры, наличием прожилок, включений и т.п.» [21]. Для использования математических методов столь конкретные свойства рисунка, как «прожилки и включения» и столь специальные как «структура и текстура» представляются неудобными. Поэтому остановимся на понятии рисунка и тех свойств, которые могут быть описаны более строго при их параметрическом отображении.
Общепринято называть рисунком изображение на плоскости, созданное средствами графики. То, чему посвящена статья, тоже традиционно называется рисунком, но имеющиеся у него особенности заставляют уточнить это понятие. Обычный рисунок всегда рукотворен. «Камень в скале» – продукт разнообразных процессов самоорганизации и дезорганизации вещества в природе, перехода подвижного состояния вещества в неподвижное, процессов дифференциации, смешения, кристаллизации, оседания зерен минералов и обломков разного размера из жидкости или воздуха, процессов жизнедеятельности, деформации и трещинообразования. Рисунок камня определяется условиями его образования, чем занимаются обширные разделы геологических наук: общая геология, геотектоника, стратиграфия, петрография и минералогия [5, 9, 11, 19]. Поэтому изображение его фрагмента – рисунка камня, как правило, не несет сходства с формами обычно выделяемых объектов. Распределение света и цвета в заготовках «цветного камня», производимых добычей, резкой и обработкой, в конечном изделии наборе, только частично, но нередко весьма значимо, результат труда человека. Поэтому же рисунок цветного камня обладает рядом особенностей, требующий к ним особого отношения. Находясь в природе, тело горной породы, вообще, не имеет определённых размеров, а потому изображение (рисунок) сечения практически всегда принадлежит фрагменту целого. В первичном залегании рисунок породы не выглядит хаотично и по-своему гармоничен, красив и естественен. Именно такой же хотелось бы видеть облицовку интерьеров. К сожалению, зачастую логика сочленения блоков отсутствует, что бывает особенно заметно в помещениях при ярком освещении, например, в метро. Это не замечается человеком, никогда не бывшим в горах, но более наблюдательным воспринимается как игнорирование природы того материала, с которым и заказчик, и дизайнер имеют дело. В геологии, в связи с относительной бедностью языка макроскопического описания камня вообще, рисунок, или его заместитель – фотография, используется часто. Это уже, как минимум, даёт возможность переноса общего мотива рисунка природного камня, наблюдаемого в геологическом обнажении, в интерьер, в изделие.
Использованию цветного камня в архитектуре, интерьерах, мелкой пластике посвящена обширная литература [2, 3, 7, 18]. При этом существует проблема измеряемого различения и систематизации рисунка пород, отличия природного камня от неприродного, а также – техническая задача – искусственного получения продукта, максимально похожего на природный. При этом количественные оценки рисунка горных пород в геологии не встречены. В то же время известно большое число способов математического описания изображений, приспособленных к определённым их типам, и использующихся в медицине, астрономии, промышленности, при автоматизации производственных процессов, и во многих других областях [8, 16, 17, 23, 25].
Как декоративный материал, использовавшийся и использующийся в предметах до сотни наименований, он может применяться и, соответственно, рассматриваться с близкого расстояния в ювелирных, настольных изделиях, и издалека, в оформлении интерьеров, а также зданий. То, что значимо для предмета в руке, на пальце, может быть совершенно неразличимым, а потому и незначимым на расстоянии десяти метров, и не подлежащим описанию.
Использование цветного камня при производстве подразумевает не единичность, и часто – массовость, и, в некоторых рамках, ограничение разнообразия рисунка. Поэтому при добыче, изготовлении деталей, пластин и использовании цветного камня как декоративного материала встаёт вопрос о необходимости систематизации его описания, чтобы из неопределенно широкого разнообразия рисунков заготовок камнецветного сырья отобрать блоки – детали – фрагменты будущего гармонически целого.
Изложенное требует несколько изменить представление о рисунке применительно к «цветному камню». Далее под «рисунком» будем понимать распределение интенсивности отраженного света и цвета в пределах выделенного участка плоскости.
Цель статьи – предложить способ параметрического – количественного описания свойств рисунков цветного камня, пригодный для их систематизации по одному параметру, принимаемому при решении конкретной задачи важнейшим.
1. Учитываемые свойства «цветного камня»
Простейшие элементы горной породы, совокупность которых порождает рисунок это: 1) зерна минералов, различающиеся по форме, цвету и блеску (примеры: гранит, лабрадорит), 2) срастания кристаллов минералов (турмалин, эгирин, малахит, селенит) 3) слои, в той или иной степени однородные (характерно для известняков, сланцев, гнейсов, турбидитов, флиша, в некоторой степени, малахита и агрегатов других минералов, обладающих «натечной», «почковидной» формами их агрегатов).
Разные образцы одной и той же породы различаются, и различные ориентации сечения одного камня могут иметь разные рисунки. Поскольку неконкретный рисунок человек воспринимает в целом, без учета мелких деталей, сжатое описание «цветного камня» должен давать обобщенное представление о многих его конкретных изображениях.
Большинство изображений, подвергаемых обработке и анализу, являются цветными. Для решения большинства задач по анализу изображений, цвет не является информативным признаком и только усложняет распознавание изображения, поэтому, как правило, его преобразовывают в полутоновое. В случаях распознавания графических образов полученное полутоновое изображение также подвергается изменениям, приводящим его в более простую форму [17]. Кроме того, в одном образце, как и в картине, могут одновременно присутствовать сильно различающиеся цвета, усреднение которых бессмысленно.
В ГОСТе 30629-99 [21] для большинства облицовочных камней представлен способ оценки его декоративности по характеру рисунка, структуре, цвету, насыщенности, светлоте и ряду других параметров. Для некоторых из них мы вводим количественные характеристики, а некоторые не учитываем (например, цвет, о котором было сказано выше).
Свойства «цветного камня», которые будут учитываться при его описании, предназначенном для систематизации, следующие:
- Светлота. Это субъективно оцениваемая яркость всего изображения по отношению к поверхности, воспринимаемой человеком как белая.
- Контраст – соотношение между максимальной и минимальной светлотами на рисунке.
- Сложность рисунка – разнообразие (в смысле К.Шеннона) светлот.
- Связность – степень коррелированности (в данном направлении) светлоты соседних элементов поверхности, с которых снимаются данные.
- Изотропия – степень близости связности в разных направлениях на рисунке.
- Ритмичность – повторение частей рисунка в каком-либо одном (или разных) направлениях.
2. Параметры рисунка и его количественные оценки
1) Светлота (Brightness – Br) является одной из характеристик цветовой системы HSB (Hue – цветовой тон, Saturation – насыщенность, Brightness – светлота) [1]. Её значение изменяется от 0 до 1, где 1 – самое высокое значение светлоты, отвечающее за белый цвет (Br=1). Формула для расчета светлоты поверхности:
![]() (1),
(1),
где B – светлота одной измерительной точки изображения (или среднее по выделенному элементу сетки), n – количество этих точек.
В качестве приёма, позволяющего обойтись без стандартизации освещенности при оценке светлоты поверхности, предлагается её сканирование при помощи планшетного сканера, либо фотосъёмка с эталоном максимальной светлоты и последующей коррекции изображения по этому эталону. В качестве эталона в наиболее простом и общедоступном варианте предлагается использовать довольно хорошо воспроизводящуюся по свойствам свежую матовую белую бумагу для принтеров. Некоторые горные породы содержат минералы, имеющие хорошую спайность, что порождает яркие, до слепящих, блики при солнечном освещении (например, полевые шпаты в гранитах типа рапакиви). Поэтому съёмку таких объектов, при оценке их светлоты, нужно производить при рассеянном свете. Коррекцию изображения можно производить в графических приложениях для ПК, например Adobe Photoshop.
2) Контраст. (Contrast – Ct). Существуют различные методы определения контраста [4]. Приведём лишь один из вариантов определения, указанный в ГОСТ 18862-73 от 1983 года.
![]() , (2.1)
, (2.1)
где Вmin и Вmax минимальное и максимальное значение светлоты участков поверхности.
Согласно формуле, чем ближе число к единице, тем меньше контраст, что нельзя считать логичным. Для приведения формулы к его интуитивному восприятию контраста достаточно вычесть (2.1) из единицы, то есть:
![]() , (2.2)
, (2.2)
Отсутствие контраста Ct=0 , одновременно, говорит и об отсутствии рисунка.
3) Сложность (Complexity - Cm) рисунка оценивается как разнообразие по К. Шеннону (1948) [10, 23, 25].
![]() , (3)
, (3)
где En – энтропия, нормированная к интервалу 0-1, pi – вероятность события – отношение суммарной площади с данной светлотой к общей площади, n – количество различимых классов событий в предлагаемом методе. Весь интервал значений светлоты рисунка делится на 10 классов (в долях единицы): 0-0.099; 0,1-0.199; 0,2-0.299, и так далее, то есть в формуле (3) n=10. Чем ближе полученное значение энтропии к единице, тем более разнообразным является рисунок. При Cm=0 имеем поле с одинаковой светлотой – рисунок отсутствует.
4) Связность. (Connectedness – Cn) Пятна одинаковой светлоты могут различаться по размерам. Рисунок с преобладанием крупных пятен можно рассматривать как рисунок с высокой связностью, то есть неразличимостью между оптическими свойствами в пределах больших участков поверхности. Преобладание мелких пятен соответствует низкой связности. Для оценки связности используется автокорреляционную функцию, которая показывает взаимосвязь между величинами исходного ряда (X) и величинами этого ряда со сдвигом (Y), называемым лагом. Коэффициент автокорреляции (КА) рассчитывается по формуле коэффициента корреляции для парной зависимости [20, 22]:
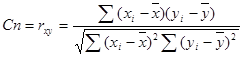 (4)
(4)
где xi и yi – значения выборки X и Y, а x̅ и y̅ - средние по X и Y.
Значение Cn в формуле изменяется от -1 до 1. Если значение по модулю находится ближе к 1, то это означает наличие положительной сильной связи, а если Cn= 0 – связь слабая или отсутствует. Знак «+» или «–» указывает на зависимость между значениями одного ряда и ряда, полученного со сдвигом на величину лага. Зависимость может быть прямая – положительная (увеличение значений в одной группе данных связано с увеличением значений в другой) или обратная – отрицательная (увеличение значений в одной связано с уменьшением значений в другой). Поскольку связность измеряется от -1 до +1, то для соизмеримости с другими характеристиками перед соотнесением этих значений они приводятся к интервалу 0-1 по формуле:
![]() (5)
(5)
5) Изотропность (Isotropy – Is). Рисунок может быть связным по-разному в разных направлениях. Так, полосчатость, обычная для осадочных и многих метаморфических пород – будет проявляться в различиях связности вдоль и поперёк слоёв. Такой рисунок, в соответствии с обычностью термина в геологии, следует назвать анизотропным. Рисунок с неразличимой связностью в разных направлениях – изотропный. Для оценки степени изотропности производятся оценки связности в двух взаимно перпендикулярных направлениях. Отношения минимальной величины к максимальной даёт оценку степени изотропии рисунка.
Изотропность определяется по формуле:
![]() (6)
(6)
Изотропность, равная единице, говорит о том, что рисунок в одинаковой степени упорядочен (как шахматная доска) или в одинаковой степени хаотичен (распределение капель дождя на поверхности).
6) Цикличность (Cyclicity – Cc) Проявляется в наличии одинаковых элементов, повторяющихся через одинаковые промежутки. Выявить цикличность рисунка позволяет использование автокорреляционных функций с порядками выше первого, то есть при коррелировании светлот с последовательно увеличивающимся лагом. При появлении максимума в такой последовательности можно говорить о существовании цикличности связностей. Если наиболее высоким оказался КА первого порядка, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался КА порядка n, то ряд содержит циклические колебания с периодичностью n. Если же ни один из КА не является значимым, то, либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию.
3. Методика подготовки и обработки изображения
Рамка анализируемого изображения имеет квадратную форму. Размер измеряемого поля рисунка соответствует размеру меньшей стороны стандартных блоков согласно ГОСТу, или среднему размеру пластин, используемых при инкрустации. Рисунок ориентирован так, чтобы его преимущественная направленность (если она существует) была ориентирована горизонтально.
На рисунок накладывается сетка, с ячейки которой снимаются значения светлоты с получением цифровой матрицы. Для измерений достаточно сетки 20x20 измерений. Необходимость изменения плотности измерений диктуется конкретными особенностями рисунка и назначением использования материала.
Снятие значений светлоты с изображения производится с использованием специальной программы BrightnessMatrix, составленной М. Д. Афанасьевым. Она автоматически генерирует цифровую матрицу, содержащую средние значение светлоты по ячейкам измерения. Есть возможность снимать результаты при помощи Adobe Photoshop, но с двумя ограничениями: а) съём значений производится с пересечений сетки, что делает результаты менее устойчивыми, б) это занимает много времени.
Поскольку автокорреляционная функция работает с рядом чисел, а не с матрицей, полученная числовая матрица светлот переводится в единый числовой ряд. Для этого производится развёртка изображения как представлено на рис. 1а, и запись числового ряда значений светлоты. Также производится развертка изображения по схеме на рис. 1б. Используя представления об изотропности, одно из направлений развёртки названо длинной осью (x), другое – короткой осью (y), где длинная ось расположена вдоль преимущественной однородности (связности) светлот рисунка.
Расчёт коэффициентов автокорреляции (КА) производится в программе Microsoft Excel при помощи встроенной функции КОРРЕЛ. Она принимает в качестве значений пару рядов, указанных со смещением.
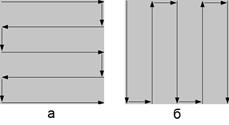
Рис. 1. Схема развёртки матрицы измерений светлоты изображения
4. Идеализированные рисунки и их анализ
Было исследовано около 50 различных тестовых изображений, из которых приведём восемь типовых (рис. 2) с результатами расчёта их параметров (табл. 1)
Изображения 1 и 2 – однотонные, простые, без рисунка. Коэффициенты автокорреляции для них невозможно посчитать, т.к. в формуле возникает деление на ноль. Такие изображения нет смысла подвергать математической обработке.
Изображения 3 и 4 представляют собой некоторую случайную мозаику из двух и трёх тонов соответственно. Связность у них близка к нулю, однако проявляется некоторая цикличность по обоим направлениям. Изотропия (хаотичность) высокая.

Рис. 2. Тестовые изображения.
Таблица 1
Результаты расчёта параметров тестовых изображений, представленных на рис. 2
|
№ |
Br |
Ct |
Cm |
Cn |
Is |
Ccxmax |
Ccymax |
|
|
x |
y |
|||||||
|
1 |
0,00 |
0,00 |
0,00 |
- |
- |
- |
- |
- |
|
2 |
1,00 |
0,00 |
0,00 |
- |
- |
- |
- |
- |
|
3 |
0,50 |
1,00 |
0,30 |
0,53 |
0,52 |
0,98 |
17 |
13 |
|
4 |
0,50 |
1,00 |
0,48 |
0,53 |
0,55 |
0,97 |
4 |
13 |
|
5 |
0,50 |
1,00 |
1,00 |
1,00 |
1,00 |
0,99 |
1 |
1 |
|
6 |
0,50 |
1,00 |
0,30 |
1,00 |
0,95 |
0,95 |
1 |
1 |
|
7 |
0,50 |
1,00 |
0,30 |
0,99 |
0,85 |
0,86 |
1 |
1 |
|
8 |
0,50 |
1,00 |
0,47 |
1,00 |
0,88 |
0,88 |
1 |
1 |
Изображение 5 – градиент, плавный переход от чёрного к белому (аналог изменения состава вещества в слое турбидита). Его связность и изотропия равны (почти равны) единице. Сложность максимальна, достигает единицы, так как все 10 групп оттенков представлены на изображении в одинаковом количестве.
Изображение 6 – некоторая аналогия изображения 5, где сохранён контраст, но убраны все промежуточные светлоты, что привело к резкому снижению сложности. Связность по длинной оси (x) практически равна единице (высокая однородность вдоль горизонтали), по вертикальной оси (y) – несколько ниже.
Изображение 7 – усложнённый вариант предыдущего, где добавлено ещё две полосы. Здесь связность по оси y значительно меньше, чем по x. Это обусловлено развёрткой изображения, а именно: в ряде измерений по оси х все значения, принадлежащие полосе, идут друг за другом, в то время как по y они разбросаны по всему ряду. Соответственно, увеличение количества полос будут снижать связность по короткой оси, а по длинной оси изменения будут малозначимыми. Отметим, что параллельное смещение положения полос не влияет на количественные характеристики результатов измерений.
Изображение 8 сходно с предыдущим, однако его сложность выше, т.к. добавляется ещё один класс светлоты.
5. Параметрическое представление реальных рисунков
Рассмотрим изображения гранитов, мраморов, природных и выращенных малахитов, а также имитации малахита (рис. 3). Изображения гранитов и мраморов взяты из книги Зискинда [6], ориентировочный размер 5х5 см, малахитов и их имитации – из личной коллекции – размер ок. 2х2 см. Расчеты параметров приведены в таблице 2.
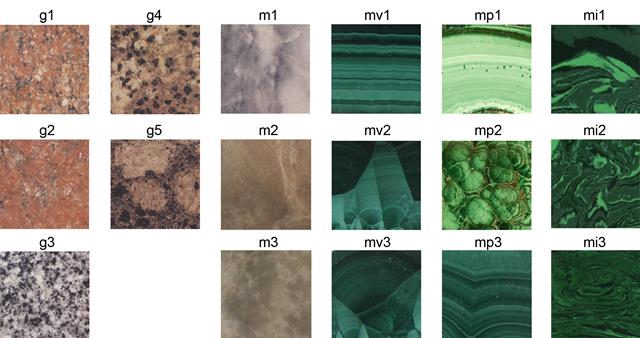
Рис. 3. Граниты (g1-g5), мрамора (m1-m3) (по Зискинду [6]), малахит выращенный (mv1-mv3), малахит природный (mp1-mp3), имитации малахита (mi1-mi3) (из личной коллекции авторов)
Таблица 2. Количественная оценка параметров изображений, представленных на рис. 3
|
№ |
Br |
Ct |
Cm |
Cn |
Is |
|
|
x |
y |
|||||
|
Граниты |
||||||
|
g1 |
0,66 |
0,40 |
0,45 |
0,73 |
0,64 |
0,88 |
|
g2 |
0,64 |
0,38 |
0,27 |
0,76 |
0,70 |
0,92 |
|
g3 |
0,55 |
0,72 |
0,67 |
0,67 |
0,67 |
1,00 |
|
g4 |
0,55 |
0,67 |
0,67 |
0,75 |
0,75 |
0,99 |
|
g5 |
0,47 |
0,71 |
0,69 |
0,91 |
0,90 |
0,99 |
|
Мрамора |
||||||
|
m1 |
0,60 |
0,45 |
0,56 |
0,96 |
0,92 |
0,96 |
|
m2 |
0,52 |
0,39 |
0,43 |
0,97 |
0,96 |
0,99 |
|
m3 |
0,51 |
0,37 |
0,37 |
0,94 |
0,91 |
0,97 |
|
Малахит выращенный |
||||||
|
mv1 |
0,33 |
0,76 |
0,60 |
0,99 |
0,83 |
0,83 |
|
mv2 |
0,32 |
0,79 |
0,63 |
0,94 |
0,96 |
0,98 |
|
mv3 |
0,27 |
0,72 |
0,48 |
0,92 |
0,94 |
0,98 |
|
Малахит природный |
||||||
|
mp1 |
0,82 |
0,72 |
0,35 |
0,97 |
0,80 |
0,82 |
|
mp2 |
0,46 |
0,77 |
0,72 |
0,83 |
0,86 |
0,96 |
|
mp3 |
0,32 |
0,53 |
0,45 |
0,97 |
0,87 |
0,90 |
|
Имитации малахита |
||||||
|
mi1 |
0,30 |
0,81 |
0,65 |
0,93 |
0,79 |
0,85 |
|
mi2 |
0,29 |
0,76 |
0,42 |
0,73 |
0,74 |
0,98 |
|
mi3 |
0,25 |
0,65 |
0,19 |
0,81 |
0,57 |
0,71 |
Изображения гранитов g1 и g2 сходны и отличаются друг от друга в целом только по сложности. Изображение g4 сходно с ними, но его сложность выше. Изображение g5 выделяется среди остальных по параметрам связности – она здесь значительно выше. Это не удивительно, поскольку на g5 представлен гранит рапакиви с резко выраженными овоидами. Изображение g3 среди гранитов оказалось самым изотропным. В целом, для гранитов обычны значения связности <0,75.
Изображения мраморов, по сравнению с гранитами, обладают меньшим контрастом и большей связностью.
Для изображений малахита природного и выращенного обычен контраст 0,6–0,8, а связность более 0,75, в чем проявляется послойность нарастания. Остальные параметры могут варьировать в широких пределах. Для изображений выращенного малахита сложность составляет 0,5–0,6 (что обусловлено ограниченностью возможностей технологии), в то время как у природного она варьирует в широких пределах. Имитация малахита отличается высоким контрастом, пониженной сложностью (мал набор цветов) и связностью (отсутствие выраженной слоистости), что выдаёт её при сопоставлении с натуральным и выращенным камнем.
В целом, для представленных фокус-групп наименьшей связностью обладают граниты и несколько имитаций малахита (<0,75). Натуральные малахиты и мрамора обладают высокой связностью (более 0,9). По изотропности наименьшее значение (0,71) оказалось у одной из имитаций малахита – рисунок хаотичен. Наибольшие значения (>0,99) – у гранитов при том, что связности изменяются в широких пределах – вариации зернистости при отсутствии следов слоистости. По сложности и контрасту самыми стабильными являются результаты по выращенному малахиту. Наименее контрастными являются мрамора (разумеется, не вообще). Что касается светлоты, то в представленном материале выращенный малахит и его имитации несколько темнее натурального камня, один из образцов которого имеет максимальное значение светлоты из всей представленной коллекции.
7. Обсуждение
Предложенный способ описания рисунков цветного камня (и, более широко – горных пород) позволяет сделать следующий шаг и предложить вариант их кодирования. Нормирование всех (кроме ритмичности) параметров к одной величине (единице) обеспечивает их соизмеримость и использование совокупности рейтинга параметров и их энтропийных характеристик в качестве кода рисунка. Коды упорядочиваются, как это многократно изложено, применительно к химическим, минеральным и иным составам [12–15, 24], что автоматически породит систематику рисунков.
Представляется полезным создание фотогалереи (базы данных) кодированных рисунков камня с генетическим их описанием и анализом связи генезиса с его математическим отображением. Для геологии подобная база – средство обучения и объективизации описания горных пород; для камнеобрабатывающих предприятий – средство систематизации разновидностей камня по рисунку непосредственно на производстве; для архитектуры – способ быстрого поиска нужных материалов для облицовки и реставрации зданий, где использование даже той же разновидности камня не даёт гарантии, что он подойдёт по рисунку и не будет выделяться на общем фоне. В этом случае речь может идти не только о природном камне, но и о любом облицовочном материале, рисунок которого является абстрактным. Что касается изотропии, то в учении о метаморфизме горных пород она может стать оценкой степени их изменения от исходно слоистых осадочных пород до потерявших её следы. Мера изотропии может использоваться, в частности, при геокартировании.
Заключение
Предложенный метод параметрического описания рисунка цветного камня находится в общем потоке работ, направленных на повышение объективности и определённости описания континуально изменчивой реальности, её систем, объектов, явлений.
Авторы благодарят М. Д. Афанасьева за составление программы BrightnessMatrix, заметно облегчившей техническую часть работы.
Рецензенты:
Бискэ Г.С., д.г.-м.н., профессор, Санкт-Петербургский государственный университет, г.Санкт-Петербург.
Франк-Каменецкая О.В., д.г.-м.н., профессор, Санкт-Петербургский государственный университет, г.Санкт-Петербург.
Библиографическая ссылка
Петров Т.Г., Шуйский А.В. ПАРАМЕТРИЧЕСКОЕ ОПИСАНИЕ РИСУНКА ЦВЕТНОГО КАМНЯ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10235 (дата обращения: 16.02.2026).



