Введение
Управление при помощи Пропорционально-Интегрально-Дифференциального регулятора (далее ПИД-регулятора) показывает хорошие результаты настройки систем автоматического управления. Однако в сложных моделях расчет параметров по формулам не дает оптимальной настройки регулятора, поскольку аналитически полученные результаты основываются на сильно упрощенных моделях объекта. Поэтому после расчета параметров регулятора выполняется его подстройка. Подстройку можно выполнить на основе правил, которые используются для ручной настройки. Эти правила получены из опыта, теоретического анализа и численных экспериментов и связаны со свойствами элементов ПИД-регулятора [1]. Дополнительная подстройка параметров регулятора сложной системы вручную – довольно непростой процесс, так как соотношение между коэффициентами регулятора играет такую же большую роль, как и величины самих параметров. Настройка компонент ПИД-регулятора требует детального математического описания системы и представлений о том, в каких условиях он будет использоваться.
Цель исследования
В данной работе рассматривается вопрос создания оптимального ПИД-регулятора системы управления квадрокоптера как сложного объекта [2], подверженного воздействию внешних возмущений. В качестве искусственной нейронной сети используется нейросеть с тремя слоями обратного распространения. Необходимо, чтобы нейросетевой регулятор осуществлял поиск оптимальных параметров регулятора в процессе обучения сети, определяя градиент изменения величины целевой функции и минимизируя ее значение.
Результаты исследования и их обсуждение
Для получения оптимального регулятора, необходимо использовать алгоритм анализа системы и затем рассчитывать коэффициенты ПИД-регулятора, что в свою очередь требует детального описания моделируемой системы. Регулятор настраивается с помощью нейросети. Структура системы управления [3] представлена на рисунке 1, где выходами нейронной сети являются коэффициенты пропорциональной, дифференциальной и интегральной составляющих регулятора.
Для того чтобы создать алгоритм нейросететвого регулятора, используем математическое описание нейрона [4]. Сумма входных сигналов нейрона j определяется следующим образом
,
где
– весовой коэффициент между нейроном iи j,θj – пороговая величина. Тогда выход нейрона j
Стоит отметить, что дискретный ПИД-регулятор описывается следующим равенством:
,
где КР, КI и КD – пропорциональный, дифференциальный и интегральный коэффициенты регулятора, соответственно;r(n) – является входным сигналом объекта управления в момент времени nT и е(n) – отклонение измеряемой величины от уставки (ошибка), е(n) = r(n) – y(n); Т – интервал времени.
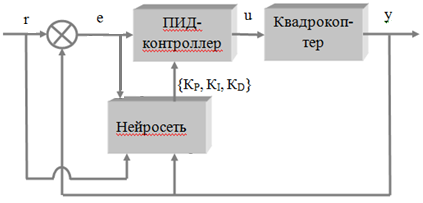
Рис. 1. Схема системы с самонастраивающимся ПИД-регулятором
Для того чтобы параметры регулятора
={КР, КI, КD} адаптировались к внешним воздействиям, применим нейронную сеть обратного распространения с тремя слоями. Значения сигналов рассогласования, использующиеся при расчете значений весов и пороговых значений нейронной сети, соответствуют значениям параметров КР, КI, КD. Для сети обратного распространения необходимо определить минимизируемую целевую функцию Е. Целевая функция выбирается так, чтобы регулятор уменьшал ошибку е(n+1) в момент времени (n+1)T [6]
где е(t, 
) – ошибка в следовании некоторой эталонной траектории с некоторым начальным возмущением, с использованием набора параметров КР, КI и КD. Допустим, что каким-то образом можно рассчитывать градиент этой целевой функции
(). В этом случае можно методом итераций улучшить параметры регулятора через определение правила обновления параметров
где (k) – вектор параметров регулятора после k итераций и α – некоторый шаг[7], определяющий коррекцию вектора параметров на каждом шаге итераций. Так как k ->
, то целевая функция E() будет приближаться к локальному минимуму в пространстве параметров регулятора.
Для того чтобы оценить (), определим
.
Зная как рассчитывать Е(
), можно численно аппроксимировать производную по отношению к любому из коэффициентов, просто рассчитывая
где
– единичный вектор в направлении К.
Так как 
, целевая функция принимает минимальное значение. Аппроксимируя значения целевой функции, можно наблюдать, как изменяется целевая функцию. Можно начать со случайно заданных положительных весов, возмущая систему в некотором установленном порядке, оценивать E(), моделируя систему с различными параметрами ПИД-регулятора, а затем рассчитать градиент. Таким образом, используя нейросеть обратного распространения [5], можно оптимизировать коэффициенты после того, как будет получена некоторая форма сходимости.
Система управления квадрокоптером на базе нейросети обратного распространения имеет несколько проблем: первая – хотя нейросетевой регулятор и находит минимум, этот минимум является только локальным минимумом и нельзя утверждать, что это оптимальное решение. Чтобы избежать выбора субоптимального локального минимума в целевой функции, требуется повторять процесс оптимизации несколько раз и выбирать лучший результат. Возможна ситуация, когда задавая различные начальные значения параметров ПИД-регулятора, будут получены различные оптимальные параметры регулятора. Кроме того, в ходе обучения нейросети используется несколько случайных возмущений во время каждого цикла и учитывается время реакции системы для расчета целевой функции и ее градиента. Это обеспечивает получение локальных оптимальных коэффициентов ПИД-регулятора при различных возмущениях, влияющих на систему. Кроме того, изменяя размер шага и количество возмущений, увеличивается чувствительность результатов во время процесса поиска коэффициентов регулятора.
Процесс поиска параметров регулятора прекращается, когда определено устойчивое состояние системы, которое достигается через расчет линейной регрессии самых последних оценок и итерации до тех пор, пока переходная характеристика не достигнет установившегося значения с погрешностью 1 % (рисунок 2).
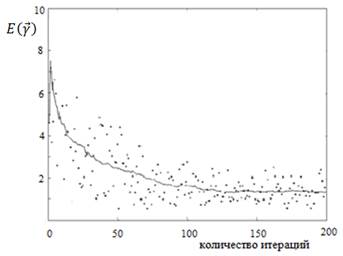
Рис. 2. График зависимости целевой функции от количества итераций
Результаты работы обычного ПИД-регулятора и нейросетевого регулятора в виде графиков переходных процессов угловых скоростей: а) обычного ПИД-регулятора и в) нейросетевого регулятора и графиков переходных процессов изменения значения углов, б) обычного ПИД-регулятора и г) нейросетевого регулятора вокруг осей, приведены на рисунках 3а-г. В процессе моделирования начальное положение квадрокоптера устанавливалось как нестабильное, и затем он должен был стабилизировать свое положение по всем значениям углов Эйлера. Из представленных характеристик видно, что преимущества нейросетевого регулятора заключаются в существенном сокращении времени переходного процесса.
Выводы
Изложенные результаты исследования позволяют сделать вывод, что система управления квадрокоптером на базе нейросетевого регулятора имеет меньшую амплитуду затухающих колебаний по сравнению с обычным ПИД-регулятором для контура скорости в 2 раза и для контура углов поворота квадрокоптера почти в 10 раз. Повышается быстродействие системы более чем в 2 раза.
К недостаткам нейросетевого регулятора можно отнести то, что для эффективной работы нейросетевого регулятора требуется довольно мощная вычислительная система, так как процесс обучения системы требует большого количества времени для проведения множества итерационных циклов.
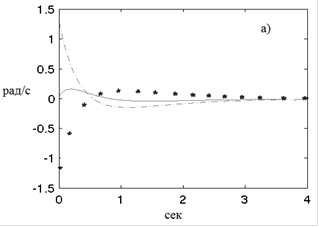
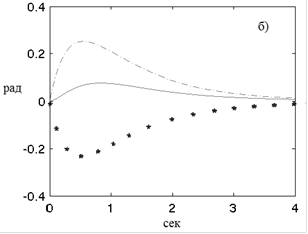
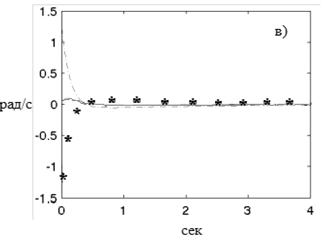
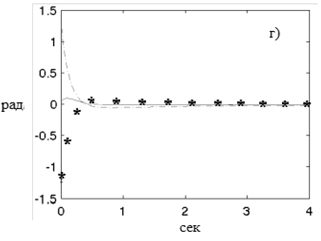
Рис. 3. Графики переходных процессов угловых скоростей и значения углов обычного ПИД-регулятора и нейросетевого регулятора вокруг осей: X – тонкая сплошная линия, Y – линия из символа“*”, Z – пунктирная линия
Таким образом, нейросетевой регулятор является более эффективным, чем ПИД-регулятор системы управления квадрокоптера, при наличии внешних возмущающих воздействий.
Статья подготовлена при поддержке Министерства образования и науки РФ в рамках проекта №11.7198.2013 по теме «Интеллектуальная система управления квадрокоптером для оценки фасадов высотных зданий».
Рецензенты:
Глебов Николай Алексеевич, доктор технических наук, профессор, профессор кафедрой мехатроника и гидропневмоавтоматики, ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М. И. Платова», г. Новочеркасск.
Шошиашвили Михаил Элгуджевич, доктор технических наук, профессор, заведующий кафедрой мехатроники и гидропневмоавтоматики, ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М. И. Платова», г. Новочеркасск.
Библиографическая ссылка
Евгенов А.А. НЕЙРОСЕТЕВОЙ РЕГУЛЯТОР СИСТЕМЫ УПРАВЛЕНИЯ КВАДРОКОПТЕРОМ // Современные проблемы науки и образования. – 2013. – № 5. ;URL: https://science-education.ru/ru/article/view?id=10222 (дата обращения: 19.04.2024).