Введение
Метод Монте-Карло – численный метод решения математических задач при помощи моделирования случайных величин, предложенный в 1949 году американскими математиками Дж. Нейманом и С. Уламом. Хотя метод был известен и ранее, но широкое применение он получил после появления ЭВМ [6]. В настоящее время метод Монте-Карло широко применяется при решении разнообразных задач многих отраслей науки и техники. Область его использования постоянно расширяется в условиях информатизации научной и производственной деятельности в связи с простым алгоритмом решения многих задач по сравнению с аналитическим решением, простотой оценок методической погрешности, слабой зависимостью точности от размерности пространства (числа независимых переменных).
В простейшем случае метод Монте-Карло состоит в синтезе математической модели объекта исследования в виде случайной величины, генерации ряда независимых испытаний (реализаций) этой случайной величины и определении статистических характеристик полученной выборки. Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. При этом метод Монте-Карло может быть использован не только для симметричных, но и для асимметричных распределений [2].
Ограничением применимости метода Монте-Карло в ходе научных исследований является то, что он не может заменить аналитические методы при исследовании малоизученных явлений и процессов, где на первом этапе необходимо выявление качественных закономерностей, описывающих объект исследования.
При проектировании измерительных устройств невозможность синтеза аналитической модели измерения не имеет значения, поскольку объект проектирования качественно определен на этапе составления уравнения измерения (функции преобразования). Последующий метрологический анализ позволяет получить оценку характеристик погрешности измерений, количественную характеристику точности, по известным характеристикам погрешности элементарных измерительных операций. Типичная методическая ошибка метода Монте-Карло 5-10% [6] полностью удовлетворяет требованиям к точности оценивания погрешности измерения.
Применение метода Монте-Карло дает наибольший эффект по сравнению с аналитическими методами при оценивании характеристик погрешности результатов косвенных, совместных и совокупных измерений, когда обрабатываются результаты прямых измерений двух и более величин.
Так, в работе [2] методом Монте-Карло получена оценка случайной погрешности произведения результатов измерений, полученных с помощью каналов измерительных систем с номинальной линейной функцией преобразования.
Аналогичные задачи возникают при разработке измерителей параметров электроизоляционных конструкций под рабочим напряжением для технического обслуживании систем электроснабжения по состоянию [5].
Материал и методы исследования
В ГОСТ 30421-96 установлены пары нормируемых электрических параметров электроизолятора, представленные в таблице 1 [3]. Пары составляют электрическая емкость ![]() или обратная ей величина
или обратная ей величина ![]() , активное электрическое сопротивление
, активное электрическое сопротивление ![]() или проводимость
или проводимость ![]() , тангенс угла диэлектрических потерь
, тангенс угла диэлектрических потерь ![]() или тангенс угла фазового сдвига
или тангенс угла фазового сдвига ![]() .
.
Значения всех нормируемых параметров электроизоляторов могут быть определены по результатам измерений активной ![]() и реактивной
и реактивной![]() составляющих комплексного сопротивления (СКС) объекта измерений и частоты ω гармонического напряжения питания измерительной схемы при использовании схемы замещения объекта в виде параллельно соединенных резистора сопротивлением
составляющих комплексного сопротивления (СКС) объекта измерений и частоты ω гармонического напряжения питания измерительной схемы при использовании схемы замещения объекта в виде параллельно соединенных резистора сопротивлением ![]() и конденсатора емкостью
и конденсатора емкостью ![]() , если оценены соответствующие характеристики погрешности. Это позволяет разработать универсальный измеритель электрических параметров электроизоляторов [1].
, если оценены соответствующие характеристики погрешности. Это позволяет разработать универсальный измеритель электрических параметров электроизоляторов [1].
Таблица 1 – Предпочтительные пары измеряемых величин
|
Предпочтительные пары |
|
|
Главная величина |
Дополнительный параметр |
|
С или 1/С С или 1/С С или 1/С R или G R или G tgδ |
tgδ R G С или 1/С tgφ С или 1/С |
Взаимосвязь нормируемых параметров электроизоляторов с СКС отражается с помощью формул:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
В соответствии с ПМГ 96-2009 в случаях, когда результаты измерений используются совместно с другими результатами измерений, за характеристики качества измерений принимают точечные характеристики - среднеквадратичное отклонение погрешности или стандартную неопределенность [4]. Точечная характеристика должна сопровождаться указанием принятой аппроксимации закона распределения плотности вероятностей погрешности. ПМГ 96-2009 распространяются на случайные погрешности прямых измерений, функции плотности распределения вероятностей которых относятся к классу симметричных, одномодальных, усеченных функций. Оценки основаны на предположениях о распределении погрешностей прямых измерений по закону равномерной плотности как наихудшему (дающему для СКО оценку сверху) из законов распределения, относящихся к указанному классу, и отсутствует корреляция между величинами, измеряемыми прямым методом и, соответственно, погрешностями их измерений.
Для оценки характеристик случайной погрешности результатов измерений параметров электроизоляторов проведено моделирование в среде MathCAD методом Монте-Карло с построением по результатам статистических испытаний гистограммы распределения плотности вероятностей случайной погрешности. Входные переменные программы: число реализаций ![]() ; число интервалов ряда наблюдений (число столбцов гистограммы)
; число интервалов ряда наблюдений (число столбцов гистограммы) ![]() ; номинальные значения СКС
; номинальные значения СКС ![]() и
и ![]() , пределы допускаемой относительной случайной погрешности СКС; математическая модель, описывающая зависимость искомой величины от СКС. Выходные переменные программы: СКО СКС, СКО искомой величины. Число реализаций определяется в зависимости от требований к точности и заранее неизвестно, оно не должно быть менее 106 .
, пределы допускаемой относительной случайной погрешности СКС; математическая модель, описывающая зависимость искомой величины от СКС. Выходные переменные программы: СКО СКС, СКО искомой величины. Число реализаций определяется в зависимости от требований к точности и заранее неизвестно, оно не должно быть менее 106 .
Для построения гистограммы использовалась встроенная функция: «hist(intvis,x)», которая определяет вектор частоты попадания данных в интервалы гистограммы; где «intvis» – вектор, элементы которого задают сегменты построения гистограммы в порядке возрастания, «a<intvisi<b;х» – вектор случайных данных. Равномерный закон распределения плотности вероятности составляющих комплексного сопротивления задавался посредством встроенной функции «runif(x1,x2,x3)». Для вычисления среднеквадратического отклонения использовалась встроенная функция «stdev(x)».
В ходе исследований было принято: ![]() ,
,![]() МОм,
МОм, ![]() МОм,
МОм, ![]() ,
,![]() Гц, пределы допускаемой относительной случайной погрешности результатов измерений СКС εRX и εXX, тангенса угла диэлектрических потерь εtgδ, тангенса угла фазового сдвига εtgφ, частоты напряжения питания измерительной схемы εω составляют ±1% номинальных значений и имеют равномерное распределение.
Гц, пределы допускаемой относительной случайной погрешности результатов измерений СКС εRX и εXX, тангенса угла диэлектрических потерь εtgδ, тангенса угла фазового сдвига εtgφ, частоты напряжения питания измерительной схемы εω составляют ±1% номинальных значений и имеют равномерное распределение.
Результаты исследования и их обсуждение
Гистограмма распределения погрешности ![]() результата измерения тангенса угла потерь
результата измерения тангенса угла потерь ![]() и погрешности результата измерения тангенса угла фазового сдвига
и погрешности результата измерения тангенса угла фазового сдвига ![]() имеет форму равнобедренного треугольника. При принятых номинальных значениях величин СКО = 0,008.
имеет форму равнобедренного треугольника. При принятых номинальных значениях величин СКО = 0,008.
Гистограмма распределения погрешности![]() результата измерения сопротивления
результата измерения сопротивления ![]() резистора эквивалентной схемы имеет форму прямоугольника, т.е. распределение равномерно, СКО = 0,012 МОм.
резистора эквивалентной схемы имеет форму прямоугольника, т.е. распределение равномерно, СКО = 0,012 МОм.
Распределение погрешности результата измерения проводимости ![]()
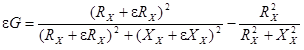 , так же как и распределение
, так же как и распределение ![]() , близко к равномерному, СКО = 2,9 мСм.
, близко к равномерному, СКО = 2,9 мСм.
Распределение погрешности результата измерения емкости ![]() эквивалентной схемы замещения
эквивалентной схемы замещения 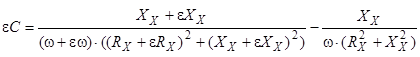 является нормальным, СКО =6,1 пФ.
является нормальным, СКО =6,1 пФ.
Плотность распределения вероятностей погрешности 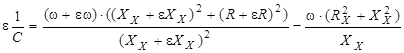 распределена нормально,СКО 1/C =3,6 1/мкФ.-
распределена нормально,СКО 1/C =3,6 1/мкФ.-
При погрешностях результатов измерений СКС более ±1% гистограммы распределения погрешностей результатов измерений величин, представленных в таблице, становятся заметно асимметричными. В этом случае при оформлении результатов измерений необходимо дополнительно указывать коэффициент асимметрии или вид закона распределения.
На рис. 1 представлена гистограмма распределения вероятности погрешности результатов измерений ![]() при εRx = 5%, εXx= ±10%, СКО
при εRx = 5%, εXx= ±10%, СКО ![]() = 0,065, коэффициент асимметрии = 0,163.
= 0,065, коэффициент асимметрии = 0,163.
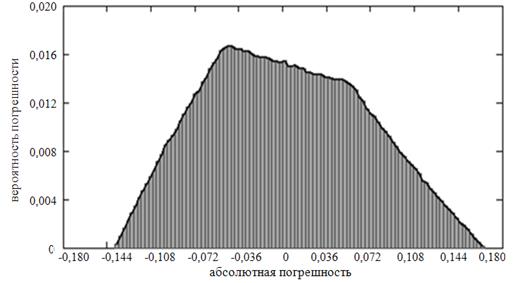
Рисунок 1. Гистограмма плотности распределения вероятностей результатов измерений tgε при εRx = 5%, εXx= ±10%.
На рис. 2 представлена гистограмма плотности распределения вероятностей результатов измерений емкости С при εRx = εXx= ±7%, СКО С=3,7 10-5 мкФ, коэффициент асимметрии = 0,152.
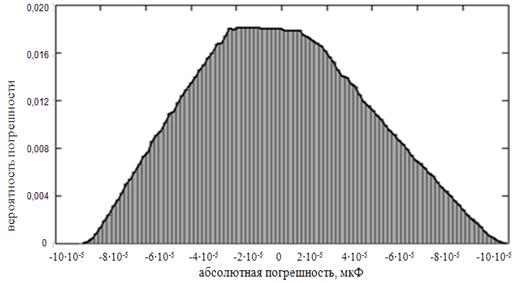
Рисунок 2. Гистограмма плотности распределения вероятностей результатов измерений емкости эквивалентной схемы замещения при εRx = εXx = ±7%.
На рис. 3 представлена гистограмма плотности распределения вероятностей результатов измерений активного сопротивления эквивалентной схемы замещения при εRx = εXx= ±7%, СКО Rx = 0,081, коэффициент асимметрии = 0,048.
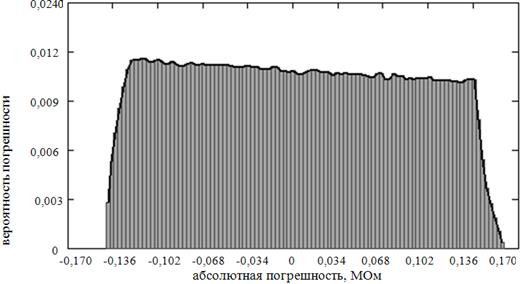
Рисунок 3. Гистограмма плотности распределения вероятностей результатов измерений активного сопротивления эквивалентной схемы замещения при εRx = εXx = ±7%.
Выводы
Метод Монте-Карло является эффективным инструментом оценивания характеристик случайных погрешностей косвенных, совокупных и совместных измерений при любых законах распределения вероятностей погрешности результатов прямых измерений, в частности среднего квадратического отклонения результатов измерений параметров комплексного сопротивления, определяющих качество высоковольтных электроизоляторов по ГОСТ 30421 - 96: электрическая емкость или обратная ей величина, активное электрическое сопротивление или проводимость, тангенс угла диэлектрических потерь или тангенс угла фазового сдвига.
Распределение плотности вероятностей погрешности результатов измерений этих параметров по значениям составляющих комплексного сопротивления, полученным прямым измерением с относительной погрешностью менее ±1% с равномерным распределением плотности вероятностей погрешности результатов измерений, является треугольным (тангенс угла диэлектрических потерь, тангенс угла фазового сдвига), равномерным (активное электрическое сопротивление или проводимость) или нормальным (электрическая емкость и обратная ей величина).
При относительной погрешности результатов измерений составляющих комплексного сопротивления, превышающей ±1%, распределения плотности вероятностей погрешности результатов измерений параметров комплексного сопротивления становятся заметно асимметричными. В таких случаях при оформлении результатов измерений необходимо дополнительно указывать коэффициент асимметрии или вид закона распределения вероятностей погрешности.
Рецензенты:
Цыпин Б.В., д.т.н., профессор, Пензенский государственный университет, кафедра «Информационно-измерительная техника»,г. Пенза.
Громков Н.В., д.т.н., профессор, Пензенский государственный университет, кафедра «Информационно-измерительная техника», г. Пенза.
Библиографическая ссылка
Баранов В.А., Данилов А.А., Шумарова С.А. ОЦЕНИВАНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ ПАРАМЕТРОВ КОМПЛЕКСНОГО СОПРОТИВЛЕНИЯ МЕТОДОМ МОНТЕ-КАРЛО // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10205 (дата обращения: 09.01.2026).



