Введение. Территорию Республики Марий Эл (РМЭ) можно приять за локальную точку на карте Российской Федерации. Для неё климатические условия приняты постоянными, а леса занимают более 54%. Следующими отличительными признаками этой точки являются малая плотность населения, компактная урбанизация, высокая экологичность территории.
Из-за экологических кризисов усиливается значение лесов в климатических технологиях и роль лесного хозяйства в динамике лесных пожаров, которые ныне сопоставимы с площадью лесов, вырубаемых для древесины. Большое количество лесных пожаров, огромные потери природных и антропогенных ценностей из-за них вызывают потребность в анализе, прогнозе и долгосрочных мерах по защите лесов. Для этого в статье предлагается методика выявления статистических закономерностей динамики численности лесных пожаров, позволяющая создать базу для ежегодного мониторинга и итерационного прогнозирования.
Концепция моделирования и исходные данные. Информационную базу для анализа и выявления волновых функций составили официальные данные территориального органа Федеральной службы государственной статистики, Министерства лесного хозяйства по РМЭ.
Всплеск количества пожаров в лесах РМЭ в 2002 г. был, по-видимому, связан с циклом солнечной активности [1; 2]. Таким образом, максимумы 1972, 2002 и даже 2010 гг. численности лесных пожаров показывают наличие пока неизвестной математической зависимости.
Однако основной причиной возникновения лесных пожаров является неосторожное обращение с огнем населения и людей, работающих в лесу. От природных гроз за 10 лет возникло всего 5,8% пожаров, но ими было погублено 28,4% от поврежденной пожарами площади леса [10]. Поэтому солнечная радиация влияет на возгораемость лесных горючих материалов [7], но количество пожаров ![]() на 94,2% зависит от человеческого фактора.
на 94,2% зависит от человеческого фактора.
Поэтому в статье время ![]() (табл. 1) принимается за главную влияющую переменную. Относительно неё затем можно дать анализ динамики солнечной активности по числам Вольфа, и только после этого можно будет браться за изучение влияния чисел Вольфа на пожары.
(табл. 1) принимается за главную влияющую переменную. Относительно неё затем можно дать анализ динамики солнечной активности по числам Вольфа, и только после этого можно будет браться за изучение влияния чисел Вольфа на пожары.
Таблица 1 - Количество лесных пожаров на гослесфонде РМЭ (с учетом НП «Марий Чодра»)
|
Год |
Время
|
Кол-во
|
Год |
Время
|
Кол-во
|
Год |
Время
|
Кол-во
|
Год |
Время
|
Кол-во
|
Год |
Время
|
Кол-во
|
|
1963 |
0 |
83 |
1973 |
10 |
84 |
1983 |
20 |
49 |
1993 |
30 |
142 |
2003 |
40 |
84 |
|
1964 |
1 |
163 |
1974 |
11 |
88 |
1984 |
21 |
88 |
1994 |
31 |
91 |
2004 |
41 |
111 |
|
1965 |
2 |
51 |
1975 |
12 |
162 |
1985 |
22 |
51 |
1995 |
32 |
233 |
2005 |
42 |
164 |
|
1966 |
3 |
168 |
1976 |
13 |
18 |
1986 |
23 |
84 |
1996 |
33 |
285 |
2006 |
43 |
218 |
|
1967 |
4 |
138 |
1977 |
14 |
63 |
1987 |
24 |
75 |
1997 |
34 |
178 |
2007 |
44 |
135 |
|
1968 |
5 |
79 |
1978 |
15 |
9 |
1988 |
25 |
199 |
1998 |
35 |
153 |
2008 |
45 |
92 |
|
1969 |
6 |
89 |
1979 |
16 |
35 |
1989 |
26 |
47 |
1999 |
36 |
226 |
2009 |
46 |
203 |
|
1970 |
7 |
66 |
1980 |
17 |
15 |
1990 |
27 |
28 |
2000 |
37 |
81 |
2010 |
47 |
437 |
|
1971 |
8 |
84 |
1981 |
18 |
190 |
1991 |
28 |
89 |
2001 |
38 |
238 |
2011 |
48 |
55 |
|
1972 |
9 |
386 |
1982 |
19 |
36 |
1992 |
29 |
195 |
2002 |
39 |
341 |
2012 |
49 |
25 |
Эту таблицу нужно ежегодно дополнять и проводить повторное моделирование с 1963 г. Статистика лесных пожаров пока имеет малую достоверность. Экологи оценивают площадь пожаров с помощью спутникового мониторинга. В разных источниках информации приводятся сильно различающиеся между собой количественные данные. Поэтому погрешность измерений можно оценивать только сопоставлением данных: для РМЭ она равна 9,1%.
Итак, погрешность измерений и регистрации количества лесных пожаров на территории РМЭ достигает 10%. Поэтому и статистическое моделирование [8; 9] нужно проводить не точнее уровня добротности таких исходных данных. Но даже при этом появляются волновые составляющие, которые дают закономерности с очень сильной теснотой связи.
Методику моделирования покажем по ходу выявления биотехнической закономерности от простого уравнения к сложной конструкции с несколькими волновыми составляющими.
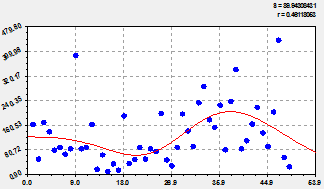
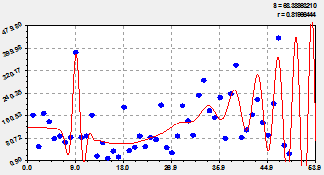
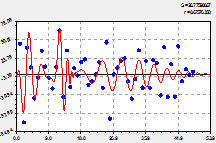
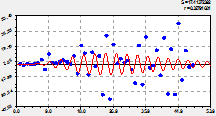
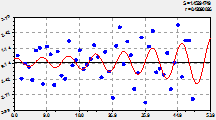
Трендовая закономерность. Она дает тенденцию до 1963 г. и после 2012 г. В программной среде типа CurveExpert вначале выявляется (рис. 1) тренд по формуле
![]()
![]() . (1)
. (1)
|
|
|
|
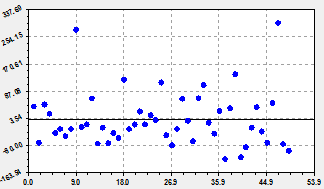
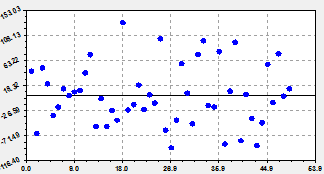
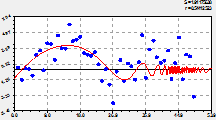
график по двухчленной формуле (1) |
остатки (абсолютная погрешность) от формулы (1) |
Рис. 1. Основная тенденция динамики численности лесных пожаров на территории РМЭ
(в правом верхнем углу графика: ![]() - дисперсия остатков;
- дисперсия остатков; ![]() - коэффициент корреляции)
- коэффициент корреляции)
Из первой составляющей формулы (1), являющейся законом экспоненциального спада [3-8], видно, что в среднестатистическом смысле за 50 лет численность лесных пожаров медленно снижается. Это естественный процесс указывает на то, что качество охраны лесов от пожаров на локальной территории медленно нарастает. Однако за период 1983-2002 гг. наблюдалось стрессовое возбуждение пожаров по второй составляющей формулы (1). Этот биотехнический закон [3] в тренде (1) характеризует антропогенное влияние, то есть влияние системного социально-экономического кризиса страны, который по графику на рисунке 1 нарастал 20 лет с 1983 по 2002 г., а потом в течение 10 лет убывает с 2002 по 2012 г.
Таким образом, в тренде (1) первый член показывает качество лесной службы, а второй член дает характеристику проявления системного кризиса со времен СССР на территории РМЭ. Поэтому тренд (1) сам по себе никакого отношения к солнечной активности не имеет.
Уровни адекватности. Адекватность предыдущего вывода является средней (табл. 2) с коэффициентом корреляции 0,4612. Но по остаткам на рисунке 1 заметно, что точки около линии регрессии по формуле (1) размещаются волнообразно.
Таблица 2 - Уровни адекватности факторных отношений
|
Интервал коэффициента корреляции |
Характер тесноты связи между факторами |
||
|
существующая классификация |
для технических экспериментов |
уточненная шкала для лесных пожаров |
|
|
1 |
сильная связь |
однозначная |
однозначная |
|
0,99…1,00 |
сильнейшая |
почти однозначная |
|
|
0,95…0,99 |
сверхсильная |
||
|
0,90…0,95 |
сильнейшая |
||
|
0,7…0,9 |
сильная |
сильная |
|
|
0,5…0,7 |
слабая связь |
средняя |
средняя |
|
0,3...0,5 |
слабоватая |
слабоватая |
|
|
0,1…0,3 |
нет связи |
слабая |
слабая |
|
0,0…0,1 |
слабейшая |
слабейшая |
|
|
0 |
нет связи |
нет связи |
|
И это позволяет дополнительно к тренду (1) идентифицировать параметры у множества асимметричных вейвлет-сигналов [4; 5], то есть совокупности волновых уравнений с переменными амплитудой и периодом. Последний и может совпадать с параметрами поведения Солнца. Для динамических рядов годичной численности лесных пожаров пришлось ввести еще два уровня адекватности, что было выполнено только при моделировании распределений рядов простых чисел [5] и параметров растущих лесных деревьев и древостоев.
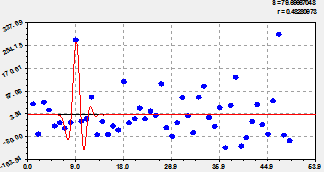
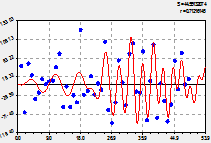
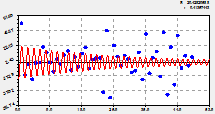
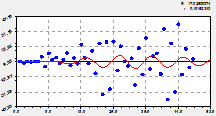
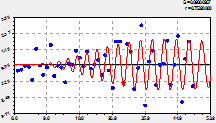
Основная модель динамики. После объединения с трендом (рис. 2) получили статистическую модель вида
![]() , (2)
, (2)
![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.
|
|
|
|
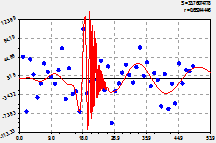
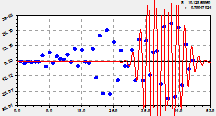
вейвлет-сигнал численности пожаров с пиком в 2002 г. |
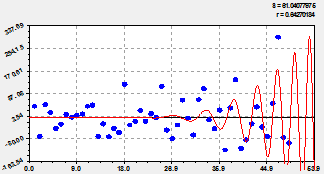
нарастающее колебание с 1988 г. на будущее |
|
|
|
|
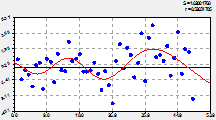
график по двухчленной формуле (2) |
остатки (абсолютная погрешность) от формулы (2) |
Рис. 2. Основная модель динамики численности лесных пожаров на территории РМЭ
Коэффициент корреляции 0,8197 выше уровня требуемой адекватности 0,7. Уравнение (2) по уровням из таблицы 2 получает сильную тесноту факторной связи. По модели (2) первое колебательное возмущение было в период с 1969 по 1974 год, то есть всего пять лет. Остатки после этой волны (второй график на рисунке 2) почти приблизились к оси абсцисс. При этом амплитуда (половина) резко возросла и затем также резко убавилась. В итоге это колебание ныне имеет только историографическую ценность, поэтому на прогноз численности лесных пожаров на территории РМЭ далее 1985 г. не влияет. Период колебания на 1963 г. был равным 2![]() 9,42545 = 18,85 года. С малой вероятностью можно допустить, что когда-то на территории марийского края периодичность скачка в количестве лесных пожаров была равна циклу обращения ядра Солнца вокруг своей оси в 22,4 года. Но к 1983 г. этот период равен нулю, поэтому вейвлет имеет антропогенный, а не гелиогенный, характер.
9,42545 = 18,85 года. С малой вероятностью можно допустить, что когда-то на территории марийского края периодичность скачка в количестве лесных пожаров была равна циклу обращения ядра Солнца вокруг своей оси в 22,4 года. Но к 1983 г. этот период равен нулю, поэтому вейвлет имеет антропогенный, а не гелиогенный, характер.
Вторая волна получает прогнозную силу с начальным в 1963 г. периодом 2![]() 4,84115 = 9,7 лет. Но до 1987 г. она имела очень малую амплитуду колебания. И только затем резко нарастет по амплитуде, при этом снижая период колебания. Процесс роста численности лесных пожаров имеет аналогию с аварийным разносом двигателя автомобиля. Территория, если не принять кардинальных противопожарных мер, может лишиться всех лесных участков с сильно горючими древостоями. Расчеты полупериода показывают, что второе колебательное возмущение прекратится только к 2060 г.
4,84115 = 9,7 лет. Но до 1987 г. она имела очень малую амплитуду колебания. И только затем резко нарастет по амплитуде, при этом снижая период колебания. Процесс роста численности лесных пожаров имеет аналогию с аварийным разносом двигателя автомобиля. Территория, если не принять кардинальных противопожарных мер, может лишиться всех лесных участков с сильно горючими древостоями. Расчеты полупериода показывают, что второе колебательное возмущение прекратится только к 2060 г.
Таким образом, оба колебания не имеют отношения к циклам солнечной активности.
Продолжение вейвлет-анализа. Остатки от (2) показали, что возможна идентификация последующих волн возмущения в динамике количества лесных пожаров за 50 лет.
Для идентификации закономерностей достаточна конструкция вейвлета типа
![]() ,
, ![]() . (3)
. (3)
где ![]() - показатель (зависимый фактор),
- показатель (зависимый фактор), ![]() - номер составляющей (3),
- номер составляющей (3), ![]() - количество составляющих,
- количество составляющих, ![]() - объясняющая переменная (влияющий фактор),
- объясняющая переменная (влияющий фактор), ![]() - параметры модели (3), принимающие числовые значения в процессе структурно-параметрической идентификации.
- параметры модели (3), принимающие числовые значения в процессе структурно-параметрической идентификации.
Параметры модели можно записать в матричной форме (табл. 3). При этом тренд есть волна с полупериодом, многократно превышающим интервал измерений.
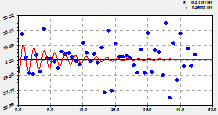
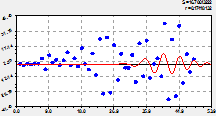
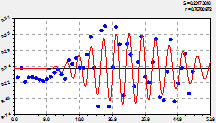
Короткомерные семь вейвлет-сигналов, находящиеся в интервале времени 50 лет и объединенные по возможностям программной среды в три подгруппы, даны на рисунке 3.
|
|
|
|
|
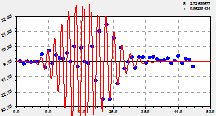
пятое и шестое колебания |
седьмое и восьмое колебания |
девятая, 10 и 11 волны возмущения |
Рис. 3. Вейвлеты коротко периодичных возмущений количества лесных пожаров на территории РМЭ
Максимальная относительная погрешность остатков после 33-го члена общей статистической модели равна 0,56% для 1978 г. Такая малая погрешность указывает на добротность исходных данных динамического ряда.
Мезоколебания. Период в 50 лет по девяти колебаниям делится на две части с границей при ![]() лет, т.е. на этапы до 1985 г. и после 1988 г. Как видно из графиков на рисунке 3, в советские времена колебания были короткими, но значительными по амплитуде. На втором этапе с 1988 г. волновые распределения характеризуются еще и значительной продолжительностью. Особенно в будущем опасна вторая волна возмущения по формуле (2).
лет, т.е. на этапы до 1985 г. и после 1988 г. Как видно из графиков на рисунке 3, в советские времена колебания были короткими, но значительными по амплитуде. На втором этапе с 1988 г. волновые распределения характеризуются еще и значительной продолжительностью. Особенно в будущем опасна вторая волна возмущения по формуле (2).
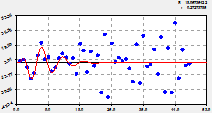
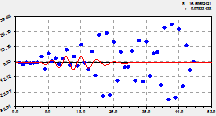
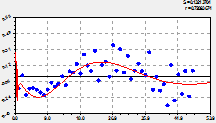
Девять колебаний по составляющим № 12-20 показаны на рисунке 4.
Таблица 3. Параметры общего уравнения динамики количества локальных лесных пожаров
|
Номер
|
Вейвлет |
Коэфф. корр.
|
|||||||
|
амплитуда (половина) колебания |
полупериод колебания |
сдвиг |
|||||||
|
|
|
|
|
|
|
|
|
||
|
Общая статистическая модель в виде тренда с двумя сильными мегаколебаниями поведения населения |
|||||||||
|
1 |
119,33947 |
0 |
0,00045832 |
2,79863 |
0 |
0 |
0 |
0 |
0,8197 |
|
2 |
1,44589e-6 |
6,92416 |
0,17190 |
0,99821 |
0 |
0 |
0 |
0 |
|
|
3 |
7,68425e-32 |
72,55620 |
11,41256 |
0,89818 |
9,42545 |
-1,42329 |
0,63075 |
-4,83945 |
|
|
4 |
-5,21468e-14 |
15,12800 |
4,36406 |
0,42474 |
4,84115 |
-0,0067929 |
1,43301 |
-0,59730 |
|
|
Короткомерные средние по амплитуде вейвлет-сигналы макроколебания численности лесных пожаров |
|||||||||
|
5 |
66986,327 |
2,70261 |
9.85601 |
0,15762 |
3,57109 |
0 |
0 |
-3,18428 |
0,7122 |
|
6 |
4,90039e-17 |
36,29153 |
19,14102 |
0,42602 |
3,71042 |
-0,13513 |
0,66273 |
-0,57666 |
|
|
7 |
3,63320e-73 |
88,24747 |
4,64148 |
1 |
39,10037 |
-1,76481 |
1 |
2,26646 |
0,6524 |
|
8 |
-0,73199 |
1,16789 |
1,13866e-5 |
2,91804 |
2,90432 |
0,13093 |
0,79788 |
5,00160 |
|
|
9 |
68,81232 |
2,41694 |
0,89851 |
1 |
1,74426 |
0 |
0 |
0 |
0,6758 |
|
10 |
-2,02491e-59 |
92,36868 |
7,51330 |
1 |
10,22157 |
-0,20384 |
1,33915 |
-1,30043 |
|
|
11 |
-2,94262e-13 |
13,85771 |
0,59207 |
0,95115 |
3,72366 |
-0,00072908 |
1,91588 |
-0,057007 |
|
|
Длинномерные мезоколебания численности лесных пожаров на локальной территории |
|||||||||
|
12 |
-9,58505 |
0 |
-0,0023738 |
1 |
-0,64111 |
1,27158 |
0,027792 |
1,27198 |
0,5444 |
|
13 |
-32522,329 |
0 |
1,10147 |
1 |
1,00090 |
0 |
0 |
-1,56976 |
|
|
Мезоколебания в виде вейвлет-сигналов о динамике численности лесных пожаров на территории РМЭ |
|||||||||
|
14 |
-719,90535 |
5,45544 |
6,20163 |
0,43033 |
3,02059 |
0 |
0 |
-1,99849 |
0,2727 |
|
15 |
0,00060255 |
5,09353 |
0,52415 |
0,78150 |
1,70572 |
-0,0065768 |
0,87771 |
-1,55638 |
0,3279 |
|
16 |
-1,64144e-5 |
7,28433 |
1,56010 |
0,59577 |
6,07694 |
-0,35954 |
0,34075 |
-3,87243 |
0,1915 |
|
17 |
7,45260e-6 |
52,76551 |
0,50131 |
1,20302 |
6,50867 |
-0,067380 |
0,97960 |
-5,58321 |
0,1742 |
|
18 |
-9,06448e-6 |
6,39989 |
0,072984 |
1,47635 |
1,86359 |
0,00016623 |
2,14254 |
0,71587 |
0,0783 |
|
Импульсные мезоколебания антропогенного влияния на количество лесных пожаров |
|||||||||
|
19 |
-3,45567e-129 |
112,73801 |
3,22205 |
0,97008 |
1,29870 |
-0,0051550 |
0,90655 |
0,82484 |
0,7905 |
|
20 |
-0,0012547 |
4,19495 |
0,0010374 |
2,51064 |
0,91814 |
0,00027857 |
1,67696 |
1,07178 |
0,9624 |
|
Микроколебания в виде длинных волн динамики возмущения численности лесных пожаров |
|||||||||
|
21 |
10,28746 |
0 |
0,068439 |
1 |
58,55825 |
-1,27230 |
1 |
1,67677 |
0,5441 |
|
22 |
-0,62738 |
0 |
-0,030047 |
1 |
7,99373 |
0,0010287 |
2,07926 |
2,39563 |
0,5265 |
|
23 |
0,30286 |
0 |
-0,035605 |
1 |
3,50130 |
0,0061667 |
1 |
0,41809 |
0,4209 |
|
Микрокороткомерные вейвлет-сигналы об антропогенном поведении в отношении к лесным пожарам |
|||||||||
|
24 |
1,17980 |
0,35553 |
0,063199 |
1 |
-0,065745 |
0,39918 |
0,35548 |
4,00313 |
0,4347 |
|
25 |
-7,20191e-5 |
6,91013 |
2,98928 |
0,44258 |
0,48188 |
0,17551 |
0,39897 |
5,57913 |
0,7533 |
|
26 |
-0,21500 |
0,25707 |
0,00017005 |
2,14277 |
4,97199 |
0,0080530 |
1,17677 |
1,80924 |
0,3178 |
|
27 |
-1,99176e-57 |
48,64450 |
1,24850 |
0,99104 |
0,58558 |
0,012897 |
0,85045 |
0,32734 |
0,7318 |
|
28 |
-0,035010 |
3,63071 |
0,57180 |
0,95239 |
1,79949 |
-0,0015890 |
1,67514 |
1,95361 |
0,5948 |
|
29 |
0,21500 |
0,19362 |
1,28367e-5 |
2,80588 |
3,17680 |
-0,00065677 |
1,31733 |
-1,87754 |
0,5278 |
|
30 |
4,11788e-7 |
26,74821 |
7,18029 |
0,81538 |
1,08407 |
-0,0067981 |
0,98302 |
0,72475 |
0,3933 |
|
31 |
1,49741e-9 |
8,80569 |
0,57154 |
0,84678 |
1,58329 |
0,00050219 |
1,46044 |
3,03251 |
0,7670 |
|
32 |
-2,67238e-7 |
11,11165 |
4,08933 |
0,52195 |
1,91371 |
0,0083175 |
0,89274 |
2,89823 |
0,7670 |
|
Сверхдлинные микроволны колебательного возмущения населения |
|||||||||
|
33 |
-0,27972 |
0 |
0,022623 |
1 |
-4,46202 |
6,03654 |
0,31842 |
3,19208 |
0,7209 |
Длинные волны № 12 и 13 остаются в прошлом. Поэтому эколого-экономическая оценка должна вестись по новой методологии, с учетом историографического анализа [6].
|
|
|
|
|
12-я составляющая модели |
13-я составляющая модели |
14-я составляющая модели |
|
|
|
|
|
15-я составляющая модели |
16-я составляющая модели |
17-я составляющая модели |
|
|
|
|
|
18-я составляющая модели |
19-я составляющая модели |
20-я составляющая модели |
Рис. 4. Вейвлеты динамического мезовозмущения количества лесных пожаров на территории РМЭ
Два импульсных мезоколебания по графикам на рисунке 4 выделяют подэтапы 1970-1999 и 1993-2015 гг., адекватность этих вейвлет-сигналов из прошлого равна 0,7905 и 0,9624. С вероятностью 79,05% кризисное (отрицательный знак перед составляющей) поведение людей в отношении к лесным пожарам с 2016 г. должно коренным образом измениться.
Микроколебания. Они опасны на будущее тем, что могут разрастись до макроуровня.
На рисунке 5 даны графики характерных по таблице 3 микроволновых закономерностей.
|
|
|
|
|
21-я составляющая модели |
22-я составляющая модели |
23-я составляющая модели |
|
|
|
|
|
25-я составляющая модели |
31-я составляющая модели |
20-я составляющая модели |
Рис. 5. Вейвлеты динамического микровозмущения количества лесных пожаров на территории РМЭ
Поэтому нужно ежегодное итеративное моделирование модели динамики. При этом 21-я волна показывает докризисное поведение: в 1990 году было минимальное количество - всего 28 лесных пожаров. Аналогия с затишьем перед бурей: хаос хозяйствования привел к увеличению количества лесных пожаров. И нарастают на будущее 22-я и 23-я составляющие, но еще долго будет значимой 25-я волна, хотя уходят в историю 31-й и 32-й члены модели. Медленно и долго уходит со сцены лесных пожаров доктрина 33 начала 60-х годов ХХ века.
Выводы. Чтобы повысить точность прогнозирования, нужно ежегодно проводить повторную идентификацию вышеприведенных формул с дополнением количества лесных пожаров, происходивших за 2013 год и так далее. Это и станет итерационным статистическим моделированием по ежегодно дополняемым статистическим данным.
Такая методика позволит гораздо точнее прогнозировать численность лесных пожаров на следующий год и тем самым заранее подготовиться к пожароопасному сезону.
Основная доля лесных пожаров происходит из-за поведения населения. На втором месте по значимости находятся грозы и молнии. Поэтому изменение амплитуды колебания по уравнениям из таблицы 3 возможно только после реализации мер по профилактике будущих лесных пожаров, снижению накапливающихся объемов лесных горючих материалов и повышению экологического сознания у населения и самих лесохозяйственников.
Рецензенты:
Салихов М.Г., д.т.н., профессор, кафедра автомобильных дорог ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола.
Колупаев Б.И., д.б.н., профессор, профессор кафедры водных ресурсов ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола.
Библиографическая ссылка
Мазуркин П.М., Каткова Т.Е. ВЕЙВЛЕТ-АНАЛИЗ МНОГОЛЕТНЕЙ ДИНАМИКИ ЛОКАЛЬНОЙ ЧИСЛЕННОСТИ ЛЕСНЫХ ПОЖАРОВ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10164 (дата обращения: 17.02.2026).