Постановка задачи
При оценке энергоэффективности работы любого электропривода целесообразно использовать оценки количества потребляемой энергии Wпот, количества энергии Wпол, затраченной на совершение полезной работы, и количества энергии ΔW, израсходованной на различного рода потери. При этом непосредственному измерению в процессе работы доступны только Wпот и Wпол, причем измерение последней в свою очередь в ряде случаев представляет собой сложную техническую задачу. Энергию ΔW непосредственно измерить невозможно, а доступным способом ее приборной оценки является тепловизорное исследование, дающее представление об интенсивности источников теплоты в электроприводе, которыми выступают потери различного рода.
В то же время для задач энергосбережения зачастую необходимо иметь количественную оценку энергии или мощности потерь, для чего, как правило, используется их математическое описание, в рамках которого выделяют потери в механических передачах, в электродвигателе, управляющем преобразователе, а также в силовых кабельных линиях. В свою очередь среди потерь энергии в электродвигателе выделяют магнитные потери (потери в стали), электрические, механические и добавочные.
Значение потерь двигателя существенно зависит от преодолеваемой им нагрузки, при этом величина электрических потерь определяется значением токов, протекающих по его обмоткам, а потери в стали для двигателей общепромышленного исполнения традиционной конструкции могут составлять более 20 % полных потерь номинального режима и более 50 % полных потерь холостого хода [1, 2]. Питание таких двигателей от полупроводниковых преобразователей увеличивает магнитные потери еще на 5–10 % [3, 4, 6].
Приведенные количественные данные получены, как правило, статистически в ходе различных лабораторных экспериментов или проведения энергоаудитов и могут использоваться только как исходные данные для постановки задачи создания энергосберегающих систем управления для электроприводов. А при непосредственном синтезе таких систем управления необходимо использовать математическое описание каждой из перечисленных выше составляющих потерь электропривода.
Следует отметить, что получение полного математического описания потерь электропривода, применимого для оптимизации системы управления электроприводом по критерию их минимума, является сложной задачей ввиду многоаспектности энергетических процессов, протекающих в рамках электромеханического преобразования энергии. Частично задача описания таких энергетических процессов может быть решена применением метода конечных элементов, однако полученные результаты, даже при достижении высокой степени адекватности, затруднительно применить для оптимизации, поскольку они представлены в форме, отличной от аналитических выражений с сосредоточенными параметрами, использующихся при управлении. В силу данных обстоятельств математическое описание потерь электропривода приводится с определенными допущениями, ограничивающими сферу их использования конкретными режимами работы. При этом одной из важных составляющих такого математического описания являются потери в стали двигателя.
Математическое описание
Потери в стали складываются из потерь на гистерезис, обусловленных расходованием энергии на преодоление остаточной намагниченности материала магнитопровода, и потерь на вихревые токи. Как правило, при расчетах мощности потерь в стали ΔPс рекомендуется использовать приближенные формулы, например, в [7] предложено следующее выражение:
![]() , (1)
, (1)
где kо – коэффициент обработки, учитывающий технологические факторы изготовления двигателя; f – частота перемагничивания магнитопровода; ΔPу – удельные потери в стали при частоте перемагничивания, равной 50 Гц; β – показатель степени, зависящий от марки стали, как правило, лежащий в пределах между 1 и 2; B – амплитуда индукция переменного поля в магнитопроводе; G – масса магнитопровода.
При их применении для регулируемого электропривода предполагают, что частота перемагничивания магнитопровода определяется угловой скоростью двигателя ω и может быть введена в расчет взамен f при условии соответствующего пересчета ΔPу.
Данный подход справедлив при длительной работе электропривода в установившемся режиме, однако в условиях работы ряда технологических установок, характеризующихся повышенной динамичностью переходных процессов, учитывая также, что для управления их электроприводами применяются полупроводниковые управляющие преобразователи, данный подход не позволит в полной мере учесть мощность магнитных потерь при решении задач энергосбережения.
Для приведения зависимости мощности потерь в стали к виду, удобному для последующего использования в таких задачах, выделим отдельно потери в стали, возникающие в статоре, и потери в стали, возникающие в роторе, мощностью ΔPс1 и ΔPс2 соответственно. Далее учтем, что индукция магнитного поля однозначно связана с потокосцеплением через площадь сечения магнитопровода и число витков обмотки, а частота перемагничивания магнитопровода пропорциональна угловой скорости вектора потокосцепления ωψ относительно угловой скорости магнитопровода. Таким образом, на основе (1) для потерь в стали ротора получим:
![]() ,
,
где ψ2 – амплитуда вектора потокосцепления ротора; p – число пар полюсов двигателя; kс2 – коэффициент потерь в стали ротора, учитывающий коэффициент обработки, удельные потери в стали, массу магнитопровода, площадь сечения магнитопровода и число витков обмотки ротора.
Данный подход предусматривает следующие допущения:
– при работе двигателя его магнитопровод находится в ненасыщенном состоянии;
– потери на гистерезис и вихревые токи рассматриваются совместно, предполагая равноценное влияние изменения потокосцепления как на одну, так и на другую составляющие потерь в стали;
– процессы перемагничивания в магнитопроводе при изменениях индукции в пределах, отличающихся от каталожных интервалов построения петли гистерезиса, происходят по малым петлям гистерезиса, площадь которых уменьшается пропорционально снижению интервалов изменения индукции.
С учетом приведенных допущений, полученная зависимость может быть выражена через переменные состояния двигателя в системе координат d-q, ориентированной по вектору потокосцепления ротора. Модель двигателя, построенная на базе уравнений обобщенной электрической машины [7], в данной системе координат описывается зависимостью:
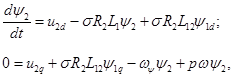
где u2d, u2q – составляющие вектора напряжения, подводимого к ротору; ψ1d, ψ1q – составляющие вектора потокосцепления статора; R1, R2 – активные сопротивления статора и ротора соответственно; L1, L2 – индуктивности обмоток статора и ротора; L12 – взаимная индуктивность обмоток статора и ротора; σ – коэффициент рассеяния, определяющийся как:
![]() ,
,
откуда получим:
![]() .
.
Таким образом, с учетом взаимного расположения векторов, получим окончательное представление мощности потерь в стали ротора, которое с учетом координатных преобразований [7] можно выразить в неподвижной системе координат α-β как:
![]() , (2)
, (2)
где ψ2α, ψ2β – составляющие вектора потокосцепления ротора.
Аналогично (2), из общего уравнения:
![]() , (3)
, (3)
где kс1 – коэффициент потерь в стали статора, идентичный по смыслу kс2; ψ1 – амплитуда вектора потокосцепления статора, с использованием системы координат, ориентированной вдоль вектора потокосцепления статора, выводится уравнение мощности потерь в стали статора в неподвижной системе координат:
![]() . (4)
. (4)
Таким образом, уравнения (2) и (4) дают полную количественную оценку мощности потерь в стали двигателя.
Анализируя эти выражения, с учетом зависимости, описывающей формирование электромагнитного момента:
![]() ,
,
можно прийти к выводу, что в динамических режимах между нагрузкой двигателя и мощностью потерь в стали существует зависимость. Тем не менее для векторных систем управления электроприводом в режиме работы, когда обеспечено приближение текущего состояния электропривода к заданным значениям M*, ψ1* или ψ2*, влияние электромагнитного момента компенсируется за счет относительного расположения векторов потокосцепления статора и ротора, а также векторов подводимого к двигателю напряжения, формирующих установившуюся частоту вращения поля статора и ротора двигателя относительно магнитопровода.
Другим важным выводом из анализа (2) и (4) является зависимость мощности потерь в стали от составляющих векторов напряжения, подводимого к двигателю, величина которых, а также интенсивность их изменения существенно зависят от особенностей системы управления конкретного электропривода. При этом для режима работы, когда текущее состояние электродвигателя приближается к заданному, на основании (1) и (3) можно утверждать, что в случае идентичного движения механической подсистемы электропривода при использовании различных векторных систем управления угловая скорость двигателя ω будет отличаться на пренебрежимо малые значения, а угловая скорость вектора потокосцепления ωψ будет определяться индивидуальными особенностями совместной работы алгоритма управления и управляющего преобразователя и при допущении идеальности последнего может быть принятой независимой от магнитного состояния двигателя, т.е. на величину магнитных потерь электропривода независимо от используемой векторной системы управления можно повлиять, изменяя ψ1*, или ψ2*, минимизируя их значение, исходя из текущего режима работы.
Вычислительные эксперименты
Для анализа применимости выражений (2) и (4) было выполнено компьютерное моделирование с использованием специально разработанного программного средства. В качестве объекта для моделирования выступала обобщенная электрическая машина с параметрами, соответствующими электродвигателю мощностью 200 кВт с учетом насыщения магнитопровода двигателя аппроксимацией кривой намагничивания полиномом четвертого порядка. В качестве системы управления электроприводом было выбрано градиентное управление [5], обеспечивающее для полностью управляемой машины переменного тока регулированное одновременно M*, ψ1* и ψ2*. Отдельно следует отметить, что эксперименты проводились как для идеализированного управляющего преобразователя, так и при учете коммутации силовых полупроводниковых ключей и ограничении максимального значения подводимого к двигателю напряжения.
В ходе экспериментов методом моделирования определялась мощность потерь в стали как сумма величин по (2) и (4), а также мощность электрических потерь в соответствии с выражением:
![]() ,
,
где i1, i2 – амплитуда векторов тока статора и ротора соответственно.
Значение использовавшихся при моделировании коэффициентов потерь в стали статора kс1 и ротора kс2 определялось аналогично номинальным потерям в стали статора в соответствии с методикой, изложенной в [1] таким образом, чтобы при номинальном режиме работы двигателя расчетное значение потерь в стали по (2) и (4) суммарно составило 20 % от значения общих потерь двигателя ΔРн, рассчитанных на основании каталожного КПД при номинальной нагрузке.
Результаты вычислительных экспериментов приведены на рис. 1 – рис. 3, где показано изменение ΔPс для одного и того же заданного состояния двигателя при идентичных настройках регулятора, используемого в градиентном управлении, в случае идеализированного управляющего преобразователя и с учетом широтно-импульсной модуляции (ШИМ) напряжения, подводимого к двигателю.
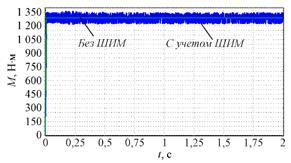
Рис. 1. Электромагнитный момент
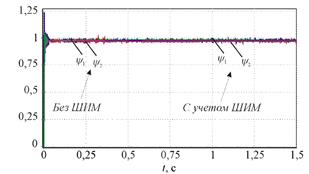
Рис. 2. Амплитуды векторов потокосцеплений
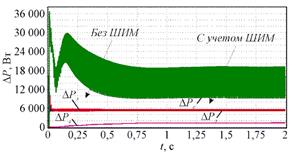
Рис. 3. Электрические потери и потери в стали
Следует отметить, что все переменные, полученные в ходе моделирования с учетом ШИМ, содержат высокочастотную составляющую, отсутствующую при идеализированном преобразователе. При этом среднее расхождение результатов моделирования, полученных с учетом и без учета ШИМ, за исключением величины ΔPс не превышает 2 %. В то же время среднее расхождение результатов моделирования по величине ΔPс составляет 830 % относительно моделирования без ШИМ. Фактически, в приведенном вычислительном эксперименте КПД двигателя, пренебрегая механическими и добавочными потерями, снизилось с 96,6 % до 90,3 %.
Данный результат подтверждает адекватность использованной математической модели вычисления потерь в стали по (2) и (4), поскольку увеличение в данных пределах магнитных потерь при использовании в качестве управляющего преобразователя полупроводниковых коммутационных устройств является общеизвестным фактом, подтвержденным многочисленными экспериментами [3, 4, 6].
Выводы
Предложенный вариант математического описания потерь в стали позволяет производить их количественную оценку методом компьютерного моделирования при использовании наиболее распространенного способа математического описания двигателя переменного тока на базе уравнений обобщенной электрической машины.
Полученный результат может быть полезен как в системах энергооптимального управления электроприводом, так и при настройке параметров управляющих преобразователей, в частности, при выборе частоты коммутации полупроводниковых ключей.
Рецензенты:
Каширских В.Г., д.т.н., профессор кафедры электропривода и автоматизации, «Кузбасский государственный технический университет имени Т. Ф. Горбачева», г. Кемерово.
Завьялов В.М., д.т.н., профессор, проректор по учебной работе, «Кузбасский государственный технический университет имени Т. Ф. Горбачева», г.Кемерово.
Библиографическая ссылка
Семыкина И.Ю. К ВОПРОСУ О МАТЕМАТИЧЕСКОМ ОПИСАНИИ ПОТЕРЬ В СТАЛИ ЭЛЕКТРОДВИГАТЕЛЕЙ ПЕРЕМЕННОГО ТОКА // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10110 (дата обращения: 17.02.2026).



