Электроэнергетическая система (ЭЭС) может быть подвержена авариям, обусловленным нарушением режима работы как самой системы, так и ее отдельных элементов. Часто последствием аварийных переходных режимов становится нарушение устойчивости ЭЭС. Данная проблема является особенно актуальной для потребителей I и II категории надежности. Нарушение устойчивости ЭЭС послужило причиной крупных аварий, как в России, так и за рубежом.
При проектировании новых ЭЭС и реконструкции действующих объектов необходимо проводить анализ устойчивости с учетом возможности утяжеления исходного нормального режима [7]. Способы утяжеления могут быть различными, а именно: снижение ЭДС источников питания, изменение конфигурации ЭЭС, изменение величины и характера нагрузок, приводящее к снижению качества электрической энергии.
Причиной снижения качества электрической энергии на крупных промышленных предприятиях является наличие в узлах нагрузок электроприемников с нелинейными вольт-амперными характеристиками [1, 5]. Такие электроприемники потребляют ток, по форме отличающийся от синусоидального. Протекание такого тока по элементам электрической сети создает в них дополнительные падения напряжения, которые приводят к искажению формы кривых тока и напряжения в системах электроснабжения [2, 8, 10].
Таким образом, задача исследования устойчивости узлов электроэнергетических систем является актуальной и требует новых решений по учету дополнительных факторов, влияющих на устойчивую работу ЭЭС. Рассмотрим нагрузку, искажающую синусоидальность форм кривых тока и напряжения.
Основным определяющим фактором при исследовании устойчивости узлов нагрузок является наличие в составе комплексной нагрузки вращающихся машин. На современных промышленных предприятиях и объектах доля потребляемой электроэнергии двигательной нагрузкой достигает 75-85%.
В теории электрических машин (в трудах Рихтера, Вольдека) показано, что при несинусоидальности питающего напряжения наибольшее влияние на момент, развиваемый асинхронным двигателем (АД) при самозапуске, оказывают высшие гармоники (ВГ), которые создают вращающие моменты, совпадающие по направлению с прямой последовательностью (рисунок 1). Гармоники, кратные трём, не создают дополнительных моментов, поэтому в данной работе мы ими пренебрегаем.
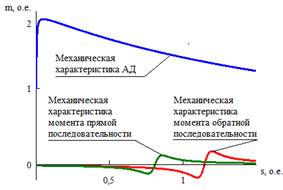
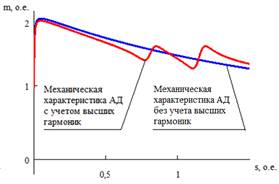
Рисунок 1 – Возникновение дополнительных моментов при несинусоидальности питающего напряжения
Искажение механической характеристики АД наблюдается при значениях скольжения, близких к единице [9].
Расчеты механических характеристик при синусоидальном напряжении и напряжении с ВГ при различных коэффициентах n -ой гармонической составляющей показали, что в диапазоне рабочей части характеристики ( s ном ≤ s ≤ s кр ) отклонение (искажение) момента несущественно.
Однако при достижении скольжения выбега АД значения от 0,7 до 1 несинусоидальность питающего напряжения оказывает существенное влияние на момент, развиваемый АД при самозапуске: отклонение может достигать 9 % от номинального (таблица 1). Это является необходимым, но не достаточным условием учета влияния несинусоидальности при расчете самозапуска.
Таблица 1 – Отклонение момента, развиваемого АД при кратности максимального момента 2,4
|
s, о.е. |
m дв , о.е. |
m дв ', о.е. |
mν, о.е. |
m Σ , о.е. |
Δ m, % |
|
0,7 |
1,631 |
1,590 |
-0,093 |
1,497 |
8,19 |
|
0,75 |
1,588 |
1,548 |
-0,094 |
1,454 |
8,45 |
|
0,8 |
1,546 |
1,485 |
0,016 |
1,501 |
2,91 |
|
0,9 |
1,47 |
1,411 |
0,089 |
1,500 |
-2,04 |
|
1 |
1,4 |
1,344 |
0,057 |
1,401 |
-0,07 |
Для нахождения результирующей механической характеристики, создаваемой основной частотой и группой ВГ, предлагаем выражение для определения момента основной частоты оставить без изменений, а моменты ВГ переписать в виде отдельной суммы сорока составляющих [3], заменив скольжение s на выражение s -( s ν - s кр ):
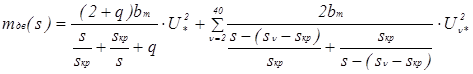 , (1)
, (1)
где bm – кратность максимального момента АД;
s – скольжение АД;
s кр – критическое скольжение АД;
U * – напряжение на основной частоте;
Uν * – напряжение на частотах ВГ;
sν – скольжение ВГ.
В результате проведенной замены характеристика моментов ВГ смещается к значению sν , полученному в теории электрических машин, а также проецируется на ось основной частоты (рисунок 2).
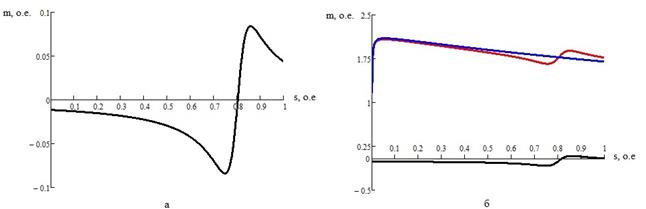
Рисунок 2 – Механические характеристики АД и дополнительных моментов от действия ВГ, рассчитанных по уточненной формуле Клосса
Таким образом, получено выражение, позволяющее рассчитывать механические характеристики АД с учетом несинусоидальности питающего напряжения.
На возможность самозапуска АД существенное влияние оказывают кратность максимального момента АД и величина начального момента исполнительного органа рабочей машины (ИОРМ): при снижении напряжения питающей сети и при наличии ВГ значения моментов механической характеристики АД при некоторых уровнях скольжения становятся меньше величин моментов ИОРМ (рисунок 3).
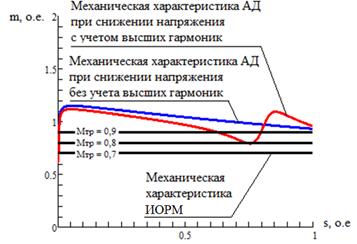
Рисунок 3 – Влияние значения начального момента ИОРМ на возможность самозапуска АД
Вышеизложенное позволяет сделать следующий вывод: если при расчете выбега скольжение ротора АД достигает значения s ≥0,7 , а также при условии просадки напряжения, несинусоидальность может стать фактором, определяющим условие возможности самозапуска АД.
С целью определения минимального напряжения, при котором возможен самозапуск АД, были построены механические характеристики АД при питании напряжением, характеризующимся различными коэффициентами несинусоидальности, и проведено сравнение с механическими характеристиками ИОРМ (таблица 2).
Таблица 2 – Минимальное напряжение, при котором возможен самозапуск АД
|
kU, % |
m тр , о.е. |
||||
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
|
U мин , о.е. |
|||||
|
0 |
- |
- |
- |
- |
- |
|
8 |
- |
- |
- |
0,76 |
0,8 |
|
12 |
- |
0,71 |
0,74 |
0,77 |
0,82 |
С учетом вышеизложенного разработана математическая модель расчета самозапуска АД, учитывающая несинусоидальность питающего напряжения. Применение этой модели позволяет уточнить минимальное значение напряжения, при котором возможен самозапуск АД.
При наличии ВГ значение активного сопротивления увеличивается пропорционально ![]() , а реактивного – пропорционально
, а реактивного – пропорционально ![]() (где ν – номер ВГ) [4]:
(где ν – номер ВГ) [4]:
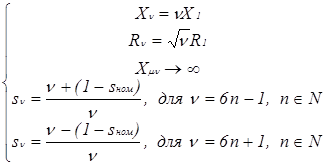 , (2)
, (2)
где R 1 , Х 1 – активное и реактивное сопротивления на основной частоте ;
R ν , Х ν – активное и реактивное сопротивления на частоте ВГ ;
Хμ ν – индуктивное сопротивление ветви намагничивания на частоте ВГ.
Для исследования влияния ВГ на характер электромагнитных переходных процессов при пуске (самозапуске) АД необходимо использовать систему уравнений (3), записанных в системе координат α, β, 0 [7]:
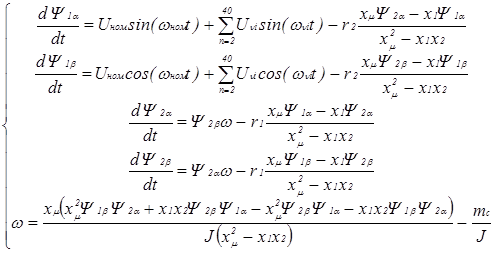 , (3)
, (3)
где Ψ1α , Ψ1β – проекции потокосцепления обмотки статора АД на оси α и β ;
Ψ2α , Ψ2β – проекции потокосцепления обмотки ротора АД на оси α и β ;
U ном – напряжение на основной частоте;
U ν – напряжение на частотах ВГ;
r 1 , х1 – активное и полное индуктивное сопротивление фазы обмотки статора АД;
r 2 , x 2 – активное и полное индуктивное сопротивление фазы обмотки ротора АД;
xμ – индуктивное сопротивление ветви намагничивания АД;
J – инерционная постоянная вращающихся масс;
mc – момент ИОРМ.
На характер изменения скорости при самозапуске окажут влияние массогабаритные параметры АД: при самозапуске более легкого АД для выхода на номинальную скорость вращения потребуется меньше времени по сравнению с более тяжелым АД, однако характер изменения скорости будет носить колебательный характер (рисунок 4).
У АД с большим значением момента инерции колебания скорости вращения при самозапуске будут менее заметны, однако увеличение массогабаритных параметров АД приведет к значительному увеличению времени самозапуска АД (рисунок 4).
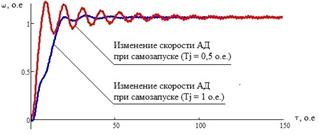

Рисунок 4 – Влияние массогабаритных параметров АД на характер изменения его скорости при самозапуске
![]() , (4)
, (4)
где Tj – электромеханическая постоянная времени;
m 'дв – момент, развиваемый АД, с учетом ВГ.
Далее выполняется проверка необходимости учета несинусоидальности при исследовании устойчивости узлов нагрузок электроэнергетических систем:
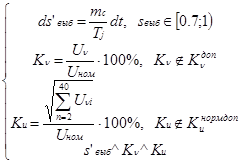 . (5)
. (5)
В случае одновременного выполнения предложенных критериев учета несинусоидальности момент АД определяется по формуле (1).
На основании полученной математической модели разработан алгоритм расчёта самозапуска АД при несинусоидальности питающего напряжения. Блок-схема алгоритма расчёта самозапуска АД при несинусоидальности питающего напряжения представлена на рисунке 5.
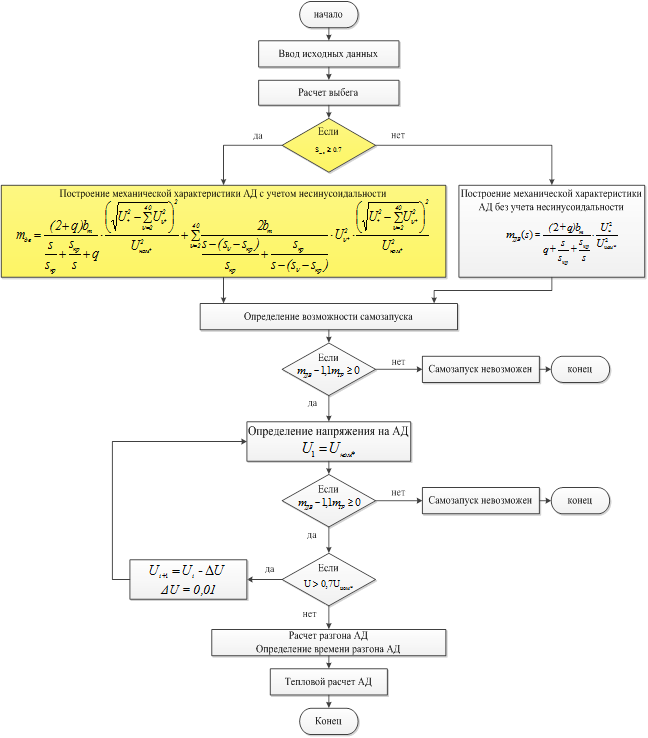
Рисунок 5 – Блок-схема алгоритма расчёта самозапуска АД при несинусоидальности питающего напряжения
Проведенные расчеты показали, что несинусоидальность приводит к значительному увеличению времени самозапуска: до 25 %, при этом нагрев АД увеличивается незначительно.
Статья опубликована при финансовой поддержке Министерства образования и науки РФ в рамках выполнения соглашения № 14.В37.21.0332 от 27 июля 2012 г.
Рецензенты:
Харламов В.В., д.т.н., профессор кафедры "Электрические машины и общая электротехника" ФГБОУ ВПО "Омский государственный университет путей сообщения", г.Омск.
Федоров В.К., д.т.н., профессор кафедры Электроники и электрификации сельского хозяйства ФГБОУ ВПО "Омский государственный аграрный университет им. П.А. Столыпина", г.Омск.
Библиографическая ссылка
Планков А.А. УЧЕТ ВЫСШИХ ГАРМОНИК ПРИ ИССЛЕДОВАНИИ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ УЗЛОВ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ С АСИНХРОННОЙ НАГРУЗКОЙ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10093 (дата обращения: 17.02.2026).



