При разработке конструкции современного металлорежущего инструмента и проектировании процесса обработки первоочередной задачей является геометрический их анализ. Косоугольное точение прямолинейным безвершинным резцом является перспективным способом чистовой механической обработки валов. Однако в настоящее время в литературе нет достаточно полного и общепринятого геометрического анализа этого способа обработки [1, 2, 4].
На основе 3D модели, представленной в работе [5], была сформирована схема процесса косоугольного точения (см. рисунок 1). Основной особенностью в данном случае является изменение статического угла наклона основной плоскости (ψс) вдоль режущей кромки в широком диапазоне (см. рисунок 1) [3]. Это вызвано изменение направления и положения вектора скорости резания (![]() ) в различных точках режущей кромки.
) в различных точках режущей кромки.
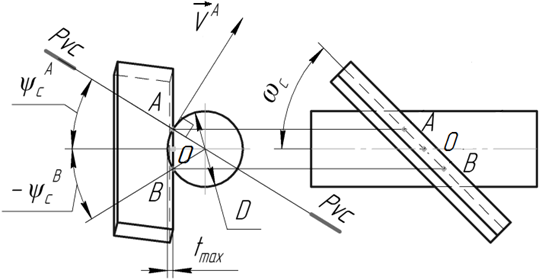
Рисунок 1. Схема определения рабочей длины режущей кромки при косоугольном обтачивании:ωс=45°; γи=-25°; αи=20°; D=20 мм; t=3 мм
Значение статического угла наклона основной плоскости в т. B определяется формулой:
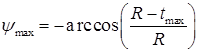 (1)
(1)
где R – радиус обрабатываемой заготовки, мм;
t –глубина резания, мм.
Значение максимальной глубины резания является непостоянным по длине режущей кромки (см. рисунок 1). Максимальное значение глубины резания определяется по формуле:
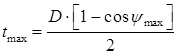 (2)
(2)
Как показано в работе [3], изменение геометрии в статической системе координат происходит в значительном диапазоне, при этом имеет место изменение знака углов. В результате чего было выявлено, что одной из проблем косоугольного точения является появление отрицательного заднего угла.
Для решения этой проблемы необходимо определить «допустимый» диапазон геометрии, то есть такой диапазон, при котором значения статического заднего угла (aс), заданные в инструментальной системе координат (aи), позволят получить значения статического заднего угла больше либо равными 1°.
С помощью зависимостей изменения геометрии, представленных в работе [3], были определены значения угла наклона основной плоскости (yсц) для различных значений угла наклона лезвия (w) и инструментальных задних углов (aи), при которых статический задний угол (aс) равен 1° (см. рисунок 2а). Определяется именно значение угла yс, поскольку он связан с основными параметрами обработки: глубиной резания и рабочей длиной режущей кромки, а также входит в уравнение, определяющее углы в статической системе координат (ССК) (aс, γс, λс, φс). Таким образом, значение ymin будет определять верхний предел изменения геометрии в ССК.
Затем были рассчитаны значения верхнего предела изменения угла в плане (φmin), угла наклона лезвия (λmin) и переднего угла (γmin) для различных углов наклона лезвия (ω) при соответствующих значениях ymin (см. рисунок 2 б-г).
а)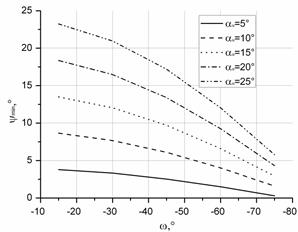 б)
б)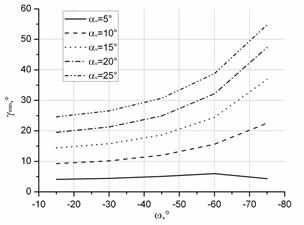
в)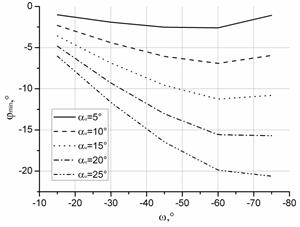 г)
г)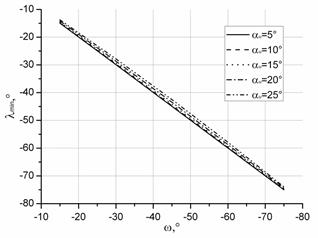
Рисунок 2. Изменение «допустимого» значения верхнего предела: а) угла наклона основной плоскости ymin;б) переднего угла γmin (при γи=0°); в) угла в плане φmin; г) угла наклона режущей кромки λminот угла наклона лезвия w при различных исходных задних углах aи
Представленные графические зависимости (см. рисунок 2) показывают, что увеличение инструментального заднего угла (aи), как и увеличение угла наклона лезвия, приводит к увеличению верхнего предела «допустимого» диапазона изменения геометрии.
Стоит отметить, что участок режущей кромки, находящийся в контакте с обрабатываемой заготовкой выше оси её вращения, будет в основном определяться значением подачи и угла ω. С учетом значения ymin можно рассчитать значения «допустимой» подачи (см. рисунок 3а), которая будет удовлетворять условию aс≥1° для различных диаметров заготовки и глубины резания:
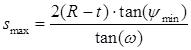 (3)
(3)
В то время как «рабочий» участок режущей кромки ниже оси вращения будет определяться диаметром заготовки, глубиной резания и статическим углом наклона основной плоскости (уравнение 1), что можно выразить уравнением:
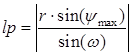 (4)
(4)
где r – радиус обработанной поверхности.
Нижний диапазон изменения геометрии будет определяться значением ψmax, причем он будет зависеть от глубины резания и диаметра заготовки, а угол ω в данном случае влияния не оказывает (см. рисунок 3б).
а)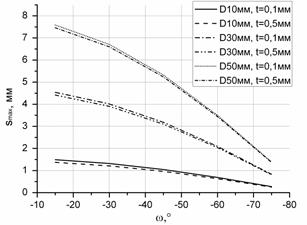 б)
б)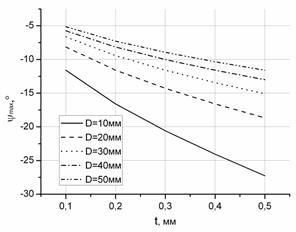
Рисунок 3. Изменение «допустимого» значения: а) подачи smax от угла наклона лезвия ω; б) нижнего предела угла наклона основной плоскости ymax
Как видно из представленных зависимостей (см. рисунок 3а), увеличение глубины резания при постоянном диаметре заготовки будет изменять значение «допустимой» подачи незначительно. Вместе с тем увеличение D приведет к значительному увеличению smax при малых значениях угла ω и к меньшему увеличению при больших значениях ω.
Увеличение нижнего предела ymax возникает при увеличении диаметра заготовки, а также с увеличением глубины резания, причем увеличение t будет сопровождаться более интенсивным увеличением ymax. Это является важным обстоятельством, поскольку, чем больше диапазон изменения угла y, тем больше и интенсивнее будут изменяться статические углы инструмента [4, 5].
После определения нижнего предела ymax по зависимостям, представленным в работе [5], можно рассчитать предел изменения геометрических параметров инструмента в ССК. В результате получены графические зависимости изменения нижнего предела «допустимой» геометрии от угла наклона лезвия (ω) при различных значениях диаметра заготовки и глубины резания, для соответствующих значений ymax, определенных из уравнения (1).
а)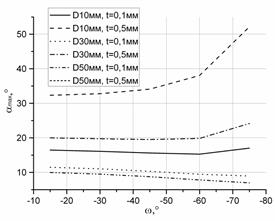 б)
б)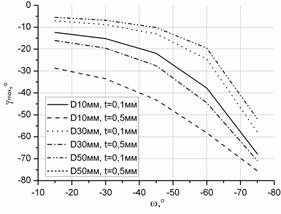
в)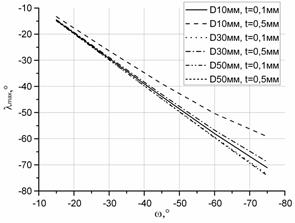 г)
г)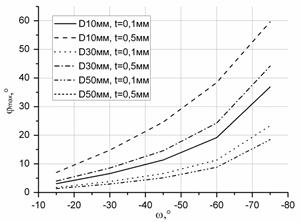
Рисунок 4. Изменение «допустимого» значения нижнего предела: а) заднего угла αmax; б) переднего угла γmax (при γи=0°); в) угла наклона режущей кромки λmax; г) угла в плане φmax от угла наклона лезвия ω
Как видно из представленных зависимостей (см. рисунок 4), увеличение угла наклона лезвия приводит к значительному увеличению нижнего предела статических углов γс, λс и φс, в то время как aс изменяется незначительно. Увеличение диаметра заготовки приведет к уменьшению нижнего предела значений углов aс, γс, и φс в большей степени, чем для угла λс. Стоит обратить внимание, что глубина резания и диаметр заготовки в целом мало влияют на изменение нижнего предела угла λс.
Также важно обратить внимание, что значения углов aс, γс, λс, φс при значениях D=10мм, t=0,1мм и D=50мм, t=0,5мм будут полностью совпадать при всех значениях угла наклона лезвия.
Еще одним важным технологическим параметром, зависящим от значения углов ψ и ω, является полная рабочая длина режущей кромки, которая находится в контакте с заготовкой в процессе обработки. Её можно определить с учетом формул (3), (4), используя следующее равнение:
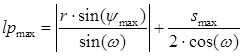 (5)
(5)
По формуле (5) были определены графические зависимости изменения lpmax (см. рисунок 5) от угла наклона лезвия при различных значениях t, smax, D для соответствующих значений ymax. Из представленной зависимости видно, что увеличение диаметра заготовки вызовет значительное увеличение lpmax при малых значениях ω и меньшее увеличение при больших ω. Увеличение глубины резания, так же как и увеличение подачи, оказывает незначительное влияние на полную рабочую длину режущей кромки.
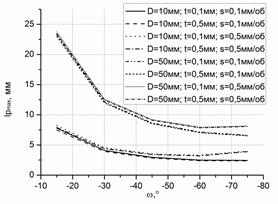
Рисунок 5. Изменение рабочей длины режущей кромки lp от угла наклона лезвия для допустимых значений угла y
Выводы
Полученные данные дают возможность выбрать технологические параметры обработки, удовлетворяющие «допустимому» значению инструментального заднего угла (aи) с учетом значений: инструментальной геометрии (aи), установочных параметров (w, tmax) и габаритов заготовки (D). Если же известны значения инструментальных углов (aи, gи), тогда задача определения геометрии сводится к нахождению «допустимых» значений tmax и w для каждого конкретного диаметра заготовки.
Как показали полученные данные, сложность выбора геометрии инструмента и параметров его установки обусловлена количеством исходных параметров и их взаимовлиянием. Значительное увеличение диапазона изменения геометрии приведет к большей неоднородности процесса обработки, что вызовет затруднения при прогнозировании качества и точности будущей детали. Назначая глубину резания и угол наклона лезвия, следует помнить, что при малых значениях угла w будет возникать проблема значительного увеличения рабочей длины режущей кромки, что может негативно сказаться на работоспособности инструмента.
Рецензенты:
Сапожков С.Б., д.т.н., профессор, заведующий кафедрой механики и инженерной графики ФГБОУ ВПО «Юргинский технологический институт (филиал) Национального исследовательского Томского политехнического университета», г. Юрга.
Петрушин С.И., д.т.н., профессор кафедры технологии машиностроения ФГБОУ ВПО «Юргинский технологический институт (филиал) Национального исследовательского Томского политехнического университета», г. Юрга.
Библиографическая ссылка
Филиппов А.В. К РАСЧЕТУ «ДОПУСТИМОЙ» ГЕОМЕТРИИ ПРИ БЕЗВЕРШИННОМ КОСОУГОЛЬНОМ ТОЧЕНИИ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10066 (дата обращения: 16.02.2026).



