Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Шевченко Н.Ю. 1 Лебедева Ю.В. 1 Хавроничев С.В. 1

---

1 ФГБОУ ВПО Камышинский технологический институт (филиал) ФГБОУ ВПО «Волгоградский государствен-ный технический университет»

В статье представлен алгоритм решения многокритериальных задач оптимизации с неопределенной ин-формацией на примере выбора оптимального варианта повышения эффективности воздушных линий электропередачи, работающих в экстремальных метеоусловиях. На основании целей функционирования воздушной линии электропередачи выбраны частные критерии оценки вариантов реконструкции. Предложены критерии эффективности: комплексный показатель надежности, отражающий безотказ-ность, долговечность и ремонтопригодность; критерий экономичности, учитывающий системный эф-фект от внедрения мероприятий, повышающих эффективность работы воздушных линий электропере-дачи, критерий технической эффективности и безопасности, учитывающий увеличение пропускной спо-собности и снижение потерь электроэнергии. Составлена целевая функция оптимизации вариантов ре-конструкции воздушных линий электропередачи.

Статья в формате PDF

227 KB

целевая функция оптимизации

система частных критериев

энергоэффективность

пропускная способность

гололедно-ветровые нагрузки

реконструкция

воздушные линии электропередачи

1. Алгоритм многокритериальных задач оптимизации с неопределенной информацией на примере выбора оптимальной мощности глубокого ввода высокого напряжения / Т. Б. Ле-щинская и [др.] // Электричество. – 2004. – № 10. – С. 8-14.

2. Левин М. С., Лещинская Т. Б. Методы теории решений в задачах оптимизации систем электроснабжения / Под ред. И. А. Будзко. – М.: ВИПКэнерго, 1989. – 130 с.

3. Лещинская Т. Б. Применение методов многокритериального выбора при оптимизации систем электроснабжения сельских районов // Электричество. – 2003. – № 1. – С. 14-21.

4. Лещинская Т. Б., Магадеев Э. В.Экспертная система оценки надежности электроснабже-ния сельскохозяйственных потребителей // Электрика. – 2008. – № 4. – С 30-35.

5. Шевченко Н. Ю. Повышение эффективности реконструируемых воздушных линий элек-тропередач, подверженных экстремальным метеовоздействиям: дис. … канд. техн. наук. – Саратов, 2011. – С. 77-84.

Разработка любой сложной системы связана с необходимостью выбора альтернатив, потому что они возникают как для системы в целом, так и для ее отдельных частей. При оценке вариантов реконструкции по многокритериальной модели необходимо учитывать специфику назначения, условия сооружения, функционирования и эксплуатации рассматриваемых систем. Решение задач оптимизации по многокритериальным моделям возможно на основе теории принятия решений. Общей методологической основой принятия решений служит системный анализ. Кроме многокритериальности задачи оптимизации характеризуются неопределенностью части исходной информации, например такой, как цены на оборудование, тарифы на электроэнергию, закон изменения электрических нагрузок, значения ущербов от перерывов электроснабжения и другие. Способ решения задач оптимизации по многокритериальным моделям в условиях неопределенности исходной информации и применяемый математический аппарат зависят от наличия и возможности получения исходной информации. В настоящее время при решении задач оптимизации нет универсальных методов снятия неопределенности среды. Существует несколько способов решения многокритериальных задач: свертка критериев в единый оценочный функционал; приоритет важнейшего критерия, метод уступок, задания уровня притязания [1, 2, .3, 4]. При свертке нескольких критериев в единый оценочный функционал применяют традиционные виды сверток: аддитивную, мультипликативную и минимаксную.

В статье представлен алгоритм решения многокритериальных задач оптимизации с неопределенной информацией на примере выбора оптимального варианта повышения эффективности воздушной линии электропередачи, работающих в экстремальных метеоусловиях [5].

1. Формулировка исходных данных. Для снятия неопределенности исходных данных рассматриваются варианты с заданными техническими параметрами: номинальное напряжение, географическое и топографическое расположение линии, общая длина рассматриваемого участка, район по гололеду и нормативное ветровое давление.

2. Обоснование цели разработки. Решение о выборе оптимального варианта реконструкции воздушной линии электропередачи (ВЛ) должно приниматься с учетом достижения различных, иногда даже противоречивых целей – Qi. Степень достижения каждой цели характеризуется количественно величиной соответствующего критерия оптимальности. Чтобы правильно сформулировать цель разработки, необходимо выяснить цель всей надсистемы и обосновать актуальность проблемы по ожидаемому вкладу в развитие энергетики. Основными целями воздушной линии электропередачи являются бесперебойное обеспечение потребителей электроэнергией высокого уровня качества с наименьшей себестоимостью передачи и распределения электроэнергии. Таким образом, можно выделить три основные цели ВЛ:

Q1 – бесперебойное обеспечение потребителей электроэнергией;

Q2 – минимальная себестоимость передачи электроэнергии;

Q3 – передача максимальной мощности с минимальными потерями.

3. Выделение объекта разработки. Данный этап содержит описание места и роли объекта в надсистеме, выделение пространственных и временных границ разрабатываемого объекта и поля поиска нового технического решения.

4. Постановка задачи: включает выделение исходных данных (неуправляемых факторов), обоснование требований к разработке и выбираемым параметрам.

5. Обоснование и выбор системы частных критериев. Выбор критериев оценки вариантов производится на основе анализа целей функционирования системы Qi. Критерии достижения целей будем называть локальными и обозначать fq, q =1…i, где q – индекс локального критерия, i – число этих критериев. Если критерии имеют различные единицы измерения, то их требуется нормализовать. Разработано большое количество схем нормализации, большинство из которых основываются на введении идеальных значений критериев , с помощью которых вектор критериев приводится к безразмерной форме – . Каждая компонента вектора может принимать значения в диапазоне (0;1).

Степень достижения каждой цели можно количественно охарактеризовать следующими критериями оптимальности: надежностью воздушной линии электропередачи fн, экономичностью fэк, и технической эффективностью fтех.эф.

Комплексный показатель надежности отражает безотказность, долговечность, ремонтопригодность ВЛ. Так как самые тяжелые последствия вызывают гололедно-ветровые нагрузки, то механический коэффициент запаса прочности кп можно рассчитать как отношение предельной толщины стенки гололеда bn , разрывающей провод при максимальной скорости и температуре воздуха – 5 0 С, к расчетной толщине стенки bp гололеда до реконструкции (). Другими показателями могут служить: снижение потокоотказов 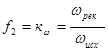; уменьшение времени восстановления поврежденного участка ; увеличение долговечности линии .

Критерий надежности примет вид:

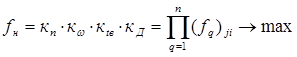(1)

Себестоимость передачи и распределения электроэнергии определяют отношением текущих затрат по передаче к количеству полезно отпущенной потребителям электроэнергии. Для ее снижения необходимо снизить потери в линии, т. е. выполнить условие . Критерием экономичности может служит максимум чистого дисконтированного дохода:

(2)

где i – номер варианта; Т – период сравнения; Д – доход от реализации электроэнергии в год t, Иijt – издержки в j-й элемент схемы в год t, – капитальные вложения в j-й элемент схемы в год t, руб.; Уti –ущерб от недоотпуска электроэнергии; Е – норма дисконта, выраженная в долях единицы или в процентах в год.

Техническую эффективность работы воздушной линии электропередачи можно характеризовать энергетическим коэффициентом кэнер и пропускной способностью по току Iпр.

Энергетический коэффициент определяет степень эффективности передачи электроэнергии и определяется по формуле:

, (3)

где – относительный коэффициент мощности, определяемый после компенсации реактивной мощности; – коэффициент полезного действия ВЛ, который определяется по выражению:

, (4)

где – нагрузка, кВт; – нагрузочные потери, кВт; ∆Ркор – потери на корону, кВт.

Тогда локальный критерий технической эффективности и безопасности:

. (5)

где f – стрела провеса провода.

6. Формулировка стратегии достижения целей. На основании имеющихся технических и экономических соображений разрабатываются возможные альтернативные варианты реконструкции линии φn , обеспечивающие достижение установленных целей. После данного этапа в распоряжении лица, принимающего решение ЛПР, оказывается матрица множества взаимоисключающих решений Ф = {φ1; φ2; φ3, φn}.

7. Оценка климатических нагрузок. Для составленных вариантов реконструкции производится оценка ожидаемых механических нагрузок на провода ВЛ при всех возможных сочетаниях климатических условий.

8. Анализ состояния среды. Средой является система явлений и параметров, влияющих на исход решения, обычно они носят неопределенный характер. В качестве среды Θ можно принять закон изменения электрической нагрузки во времени. Дополнительная информация может быть получена в виде статистической или экспертной оценки.

9. Расчет матриц значений частных критериев. Производим оценку полезности решения разработанных стратегий φ1 ÷ φn с помощью ПЭВМ и составляем матрицы частных критериев f1, … fi . Все семейство решений описывается матрицей решений (табл. 1), содержащей n-вариантов решений и m- состояний среды.

Таблица 1

Матрицы частных критериев оценки вариантов

10. Выбор способа свертки частных критериев в единый оценочный функционал. При свертке нескольких критериев в единый оценочный функционал применяют традиционные виды сверток: аддитивную, мультипликативную и минимаксную. В результате данного этапа получается матрица оценочного функционала (табл. 2). F = {Fin}, характеризующего «выигрыш»/ «проигрыш» при выборе решения φnФ, если среда будет находиться в состоянии при этом Fin = f(φn; m).

Таблица 2

Матрица оценочного функционала

11. Выбор оптимального решения. Вид оценочной функции определяется позицией ЛПР (лицо, принимающее решение).

Оптимистическая позиция ориентирует на выбор варианта с максимальной полезностью. Оценочная функция примет вид:

. (6)

Пессимистическая позиция ориентирует на выбор варианта с максимальной полезностью при наихудших условиях. Оценочная функция:

. (7)

Нейтральная позиция ориентирует на выбор варианта с максимальной средней полезностью по оценочной функции:

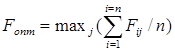. (8)

Существует множество критериев выбора лучшего решения по матрице оценочного функционала.

При дискретно заданных вероятностях наиболее устойчивым и обоснованным является критерий Байеса – Лапласа, согласно которому оптимальным становится решение, соответствующее максимуму (минимуму) математического ожидания оценочного функционала:

, (9)

где рj – вероятность проявления среды; m – число рассматриваемых изменений среды; Fi – значение оценочного функционала при i-м темпе роста нагрузки.

Оптимальным считается решение, обеспечивающее наибольшее приближение к заранее сформулированным целям.

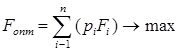. (10)

12. Обоснование принятия решения производится с учетом требований заказчика.

13. Рассчитываются показатели экономической эффективности выбранного варианта реконструкции: срок окупаемости, индекс доходности, интегральный эффект, рентабельность.

Блок-схема разработанного алгоритма представлена на рис. 1.

Вывод

Дальнейшее развитие и совершенствование теории принятия решений в условиях неопределенности зависит от накопления опыта решения многокритериальных задач в энергетике. Для повышения эффективности и объективности принимаемых решений необходим комплексный подход к формулированию и применению принципов оценки эффективности инвестиций в проекты реконструкции. В качестве указанных принципов можно рекомендовать: принцип доминирования, Парето, формирование комплексных показателей, выделение главного показателя и перевод остальных в разряд ограничений, отбор недоминирующих альтернатив, аддитивной свертки.

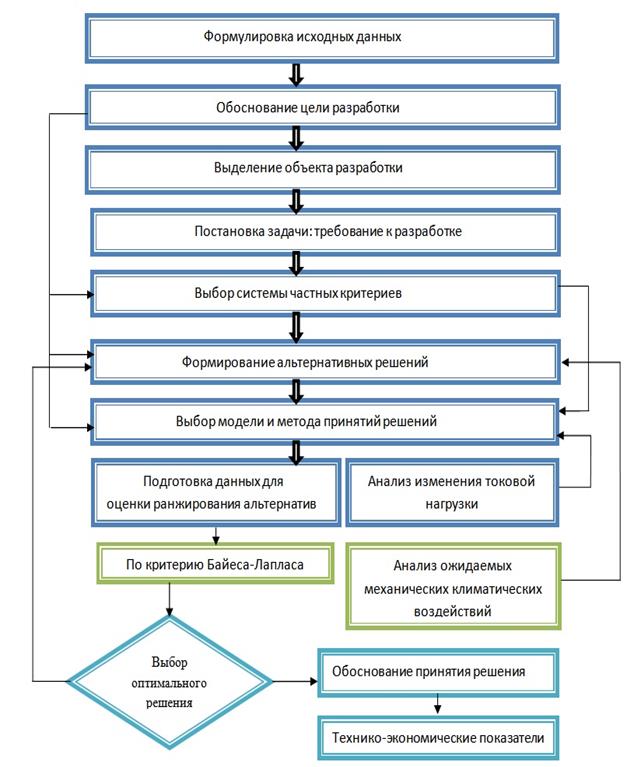
Рис. 1. Блок-схема алгоритма решения многокритериальной задачи

Рецензенты:

Артюхов И. И., д.т.н., профессор, заведующий кафедрой ЭПП СГТУ, Саратовский государственный университет, г. Саратов.

Угаров Г. Г., д.т.н., профессор кафедры ЭПП СГТУ, Саратовский государственный университет, г. Саратов.

Библиографическая ссылка