Введение
Экономическое развитие государства напрямую связано с развитием и совершенствованием машиностроительной отрасли производства. Создание новых машин и механизмов возможно только на основе серьезного научного фундамента, позволяющего обеспечить высокую эффективность машин самого различного назначения уже на стадии их проектирования.
Настоящее исследование проводится с целью создания (синтеза) механизмов для обработки сложных внутренних поверхностей деталей машин переменного сечения, а также их дальнейшего кинематического анализа. В таких механизмах обрабатывающему элементу – резцу должно быть задано движение по сложной винтовой траектории, осью которой не является прямая линия, в связи с чем применение обычных винтовых механизмов не позволяет решить такую задачу.
Для достижения поставленной цели в наибольшей степени пригодными являются механизмы второго семейства [1], звенья которых в полном декартовом пространстве имеют четыре относительных движения, либо неодносемейственные (комбинированные) механизмы [2], включающие в свой состав не только механизмы второго семейства, но и механизмы иных семейств.
Методы исследования, применяемые в настоящей работе, основаны на принципах теории структурного синтеза механизмов при использовании универсальной структурной системы; на методах аналитического исследования кинематики механизмов; приемах конструирования деталей машин.
Структурно механизмы второго семейства описываются формулой [1, с. 87]
![]() , (1)
, (1)
в которой обозначенными являются: W2 – подвижность механизма, определяющая число его степеней свободы, n – число подвижных звеньев механизма, р5, р4 и р3 – числа кинематических пар пятого, четвертого и третьего классов. Записав формулу (1) совместно с универсальной структурной системой профессора Дворникова Л.Т. [3], получим
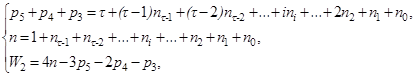 (2)
(2)
где τ – параметр, определяющий сложность базисного звена цепи – от двухпарного (τ=2), трехпарного (τ=3) и т.д. до наиболее сложного; ni – число звеньев, добавляющих в цепь по i кинематических пар.
Очевидно, что наиболее простым механизмом второго семейства будет такой, в котором будут присутствовать только пары пятого класса (р5), а базисное звено τ будет двухпарным (τ=2). Тогда при заданных параметрах, а также при W2=1 и n0=0, т.е. при отсутствии в цепи звеньев, не добавляющих кинематических пар, система уравнений (2) запишется в виде
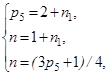
откуда из второго уравнения выразим параметр n1 и введем его первое уравнение. Далее полученное выражение для р5 подставим в третье уравнение системы и определим, что n=4, тогда р5=5. По найденному решению был построен механизм для воспроизведения пространственных кривых [4] (рис. 1), новизна которого защищена патентом РФ. Механизм относится ко второму семейству и состоит из одного неподвижного звена – стойки 1 и четырех подвижных – кривошипа 2, шатуна 3, гайки 4 с резцом R и коромысла 5. Механизм позволяет воспроизводить сложное винтовое движение выходного звена (гайки 4) с резцом R, необходимое для обработки внутренних поверхностей деталей машин.
Преобразуем этот механизм путем добавления дополнительного звена - ползуна. Присоединим коромысло через вращательную кинематическую пару к ползуну, выполненному в виде штока с поршнем, входящим с гидроцилиндром, установленным на стойке, в поступательную пару. Полученный механизм (рис. 2) носит название пространственно-геликоидного (решение о выдаче патента РФ по заявке № 2011152125 от 26.07.2013) потому, что резец R, установленный на гайке 4, совершает сложное винтовое движение по геликоидальной траектории [5].
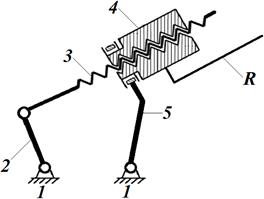
Рис. 1. Механизм для воспроизведения пространственных кривых
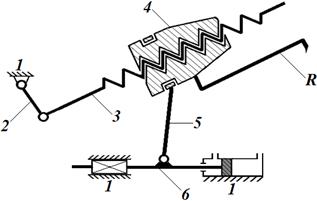
Рис. 2. Пространственно-геликоидный механизм
В состав механизма входит пять подвижных звеньев (n=5), соединенных шестью кинематическими парами пятого класса (р5=6), тогда число степеней свободы этого механизма определится из формулы (1)
W2=4n–3p5=4∙5–3∙6=20–18=2,
т.е. механизм имеет две степени свободы, и движение в нем одновременно задается двум звеньям – кривошипу 1 и ползуну 6 (подачей жидкости в поршневую или штоковую область гидроцилиндра).
Вернемся к схеме механизма для воспроизведения пространственных кривых и преобразуем ее снова, а именно присоединим коромысло через вращательную кинематическую пару к ползуну трехзвенного механизма четвертого семейства (рис. 3) с подвижностью, равной единице (W4=1). Синтезированный таким образом механизм показан на рис. 4 – это механизм для обработки сложных внутренних поверхностей, кинематическая схема которого защищена патентом РФ [6].
![]()
Рис. 3. Трехзвенный механизм четвертого семейства

Рис. 4. Механизм для обработки сложных внутренних поверхностей
Механизм является неодносемейственным, т.е. включающим в свой состав механизмы разных семейств – второго и четвертого. Звенья 1, 2, 3, 4 и 5 образуют механизм второго семейства, подвижность которого определяется по формуле (1):
W2=4∙4–3∙5=16–15=1.
Звенья 1, 6 и 7 образуют механизм четвертого семейства, подвижность которого может быть сосчитана по формуле [1, стр. 89]:
W4=2n–p5=2∙2–3=1.
Таким образом, общая подвижность механизма для обработки сложных внутренних поверхностей оказывается равной
W=W2+W4=1+1=2,
то есть этот механизм имеет две степени свободы, и движение в нем задается одновременно двум звеньям: первое - кривошипу 2, второе - ползуну 6 от двигателя 8 через винт 7, причем оба задаваемых движения могут быть направлены как в одном, так и в противоположных направлениях друг относительно друга.
Обратимся к кинематическому анализу разработанных механизмов:
- механизма для воспроизведения пространственных кривых (рис. 1);
- пространственно-геликоидного механизма (рис. 2);
- механизма для обработки сложных внутренних поверхностей (рис. 4).
Целью исследования кинематики этих механизмов является определение траектории движения их резцов R. Исследование проводилось с применением программного комплекса T-FLEX, позволяющего отследить изменение декартовых координат резцов R (XR, YR, ZR) во времени. В программном комплексе были разработаны трехмерные параметрические модели механизмов, собранные из отдельных звеньев, соединенных между собой посредством сопряжений и взаимного расположения осей.
На рис. 1 показана трехмерная модель механизма для воспроизведения пространственных кривых и траектория движения резца R, построенная по результатам расчета, приведенным в таблице 1.
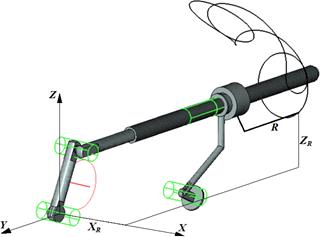
Рис. 5. Траектория движения резца R механизма для воспроизведения пространственных кривых
Таблица 1. Анализ траектории движения резца R механизма по рис. 5
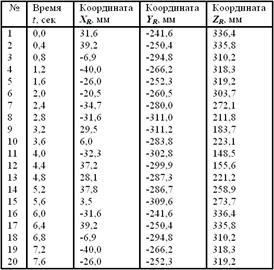
Трехмерные модели пространственно-геликоидного механизма и механизма для обработки сложных внутренних поверхностей с полученными траекториями движения их резцов приведены на рис. 6 и 7. В таблицах 2 и 3 соответственно даются числовые значения координат ХR, YR и ZR в зависимости от времени.
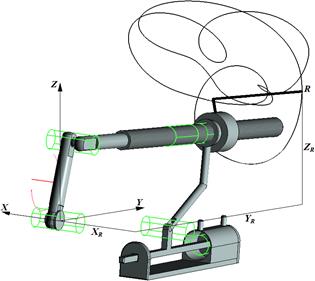
Рис. 6. Траектория движения резца R пространственно-геликоидного механизма
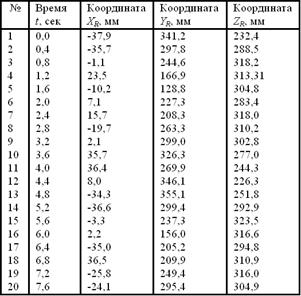
Таблица 2. Анализ траектории движения резца R механизма по рис. 6
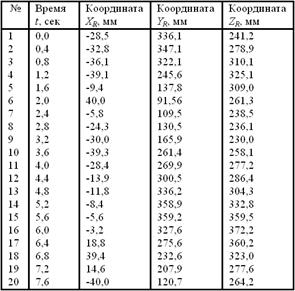
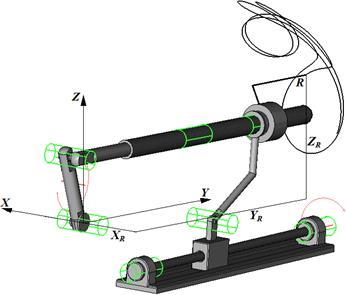
Рис. 7. Траектория движения резца R механизма для обработки сложных внутренних поверхностей
Таблица 3. Анализ траектории движения резца R механизма по рис. 7
Заключение
Таким образом, в ходе проведенного исследования были разработаны три новые кинематические схемы механизмов для обработки сложных внутренних поверхностей деталей машин переменного сечения, новизна которых подтверждается патентами Российской Федерации. Создание трехмерных параметрических моделей разработанных механизмов позволяет не только определить их кинематические параметры и выявить траекторию движения режущего элемента, но и решить другую важную задачу, а именно: по заданной поверхности подобрать параметры механизма, обеспечивающие требуемое движение резца.
Работа выполнена при финансовой поддержке в форме гранта DAAD и Министерства образования и науки Российской Федерации по программе «Михаил Ломоносов» (регистрационный № 11.7190.2013).
Рецензенты:
Дворников Леонид Трофимович, д.т.н., профессор, действительный член Международной Академии наук высшей школы, заведующий кафедрой теории механизмов и машин и основ конструирования, ФГБОУ ВПО «Сибирский государственный индустриальный университет», г.Новокузнецк.
Живаго Эдуард Яковлевич, д.т.н., профессор, заведующий кафедрой теоретической механики, ФГБОУ ВПО «Сибирский государственный индустриальный университет», г. Новокузнецк.
Библиографическая ссылка
Фомин А.С., Парамонов М.Е. СИНТЕЗ И КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ ДЛЯ ОБРАБОТКИ СЛОЖНЫХ ВНУТРЕННИХ ПОВЕРХНОСТЕЙ ДЕТАЛЕЙ МАШИН // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10044 (дата обращения: 17.02.2026).



