Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

На современном этапе реформирования российского высшего образования Министерство образования и науки РФ разработало перечень критериев, по которым будет оцениваться эффективность деятельности вузов [8] и приниматься решения об оптимизации сети вузов и их финансировании. Образовательную деятельность предлагается оценивать, в частности, средним баллом ЕГЭ зачисленных студентов (mЕ). Такой рейтинг [6], показывающий уровень знаний абитуриентов 2012 г., поступивших на бюджетные места в государственные вузы страны, возглавляют лидер социально-экономических вузов МГИМО (1-е место) и лидер технических вузов МФТИ (2-е место), а у лидера классических университетов МГУ – 7-е место. При реорганизации сети вузов РФ предполагается изменение механизма перераспределения средств в государственном секторе образования таким образом, что финансирование вуза будет зависеть, в частности, от качества сформированного им контингента студентов, то есть от рейтинга вуза по mЕ. В данной работе предлагается модель перераспределения существующей системы финансирования вузов на основе их кластеризации в пространстве показателей вступительных испытаний (ПВИ).

Своеобразие текущего момента преобразования существующей системы финансирования вузов [5; 7; 9; 10] состоит в переходе от сметного финансирования к поэтапному нормативно-подушевому финансированию государственных услуг в сфере образования, осуществление которого в полном объеме планируется к 2016 году [2-4]. Применение нормативно-подушевого метода финансирования вузов, во-первых, должно дать импульс к возникновению конкуренции вузов за «бюджетных» студентов и способствовать повышению качества образования, и, во-вторых, за счет управления значениями дифференцированных нормативов позволит осуществлять поддержку отдельных направлений высшего профессионального образования, которые являются социально значимыми и важными в свете реализации программ инновационного развития экономики РФ. Чтобы рассчитать необходимый для конкретного вуза объем финансового обеспечения выполнения государственного задания на оказание образовательных услуг, базовый норматив умножается на контингент обучающихся по данной специальности и на соответствующие корректирующие коэффициенты, отражающие стоимость обучения по группе специальностей и особенности положения вуза [3], а также качество предоставляемых вузом образовательных услуг [9]. Такой подход к формированию субсидий на выполнение государственного задания, во-первых, основывается на общих нормативных правовых актах и, во-вторых, учитывает специфику положения образовательных учреждений. Модель нормативно-подушевого финансирования вуза с дифференцированными нормативами можно задать следующей формулой:

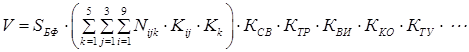, (1)

где V – объем бюджетного финансового обеспечения выполнения государственного задания на оказание образовательных услуг;

SБФ – базовый (минимальный) подушевой норматив, равный медианному значению стоимости обучения бакалавра по специальностям первой стоимостной группы, составивший 60,2 тыс. рублей (в расчете на студента первого курса 2012/2013 учебного года) [3] и включающий затраты, непосредственно связанные с оказанием образовательной услуги (57,5 %), на общехозяйственные нужды (35,5%) и прочие расходы;

Кij – повышающие коэффициенты для разного уровня ВПО (: бакалавриат, специалитет и магистратура) и разных стоимостных групп специальностей ( в зависимости от потребностей материально-технической базы обучения и стоимости годовой подготовки в расчете на одного студента), различающиеся по уровням образования бакалавров и специалистов (от 1,00 до 1,86) и магистров (от 1,17 до 2,12) [3];

Кk – коэффициент дифференциации формы обучения (: К1 = 1,0 – очная, К2 = 0,4 – очно-заочная, К3 = 0,2 – заочная, К4 = 0,2 – экстернат, дистанционная) [3];

– контингент обучающихся по данной стоимостной группе специальностей () с учетом уровня ВПО () и формы обучения ();

КСВ – повышающий коэффициент статуса вуза, т.е. принадлежности к категории «федеральный университет» или «национальный исследовательский университет», где затраты на обучение выше (на 20–60%), чем в большинстве вузов, не имеющих такого статуса;

КВИ – повышающий коэффициент качества набора по результатам вступительных испытаний;

ККО – повышающий коэффициент качества предоставления образовательной услуги;

КТУ – повышающий коэффициент качества выпуска.

Заметим, что в ходе реформы системы финансирования вузов не исключаются корректировки как в составе индексных коэффициентов стоимостных групп специальностей (Кij и Кk), так и в составе литерных корректирующих коэффициентов особенностей положения вуза (КСВ, КТР, КВИ, ККО, КТУ и т.п.).

В связи с рассматриваемой моделью (1) представляет интерес рассмотренная в данной работе методика расчета повышающего коэффициента качества набора КВИ. Предлагается следующая формула вычисления:

, (2)

где Δ определяется из соображений приоритетности показателя качества набора с учетом объема экономии средств, а R рассчитывается на основе кластеризации вузов в пространстве ПВИ.

Простейший вариант пространства вступительных испытаний – рейтинг вузов по mЕ [6] (рис. 1). Можно ввести, например, 4 категории уровней качества набора по результатам mЕ 2012 г., характеризующиеся соответствующим балльным интервалом, средним m значений mЕ интервала, числом n вузов в интервале и относительным расстоянием категорий R = (m- mmin)/( mmax- mmin), где mmax и mmin наибольшее и наименьшее значения m (табл. 1).

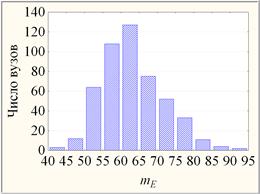
Рис. 1. Гистограмма распределения вузов по mЕ 2012 г. по 100-балльной шкале.

Таблица 1 – Характеристики 4-уровневой номинальной шкалы качества набора по результатам mЕ 2012 г.

Например, при Δ=0,20 согласно табл. 1 по формуле (2) можно вычислить соответствующие разным уровням качества набора значения коэффициента КВИ : 1,20 для уровня «лидер»; 1,12 для уровня «высокий»; 1,052 для уровня «средний» и 1,00 для уровня «низкий».

Далее рассмотрим вариант более емкой кластеризации вузов в двухмерном пространстве ПВИ, состоящем из сводного индекса качества приема (СИКП) студентов 2010 года и динамического показателя разности в средних баллах ЕГЭ среди зачисленных по конкурсу в 2011 и 2010 годах (DmЕ) [6]. Показатель СИКП учитывает средние баллы ЕГЭ студентов, зачисленных в вузы на бюджетные места, средние баллы ЕГЭ студентов, зачисленных в вузы на коммерческие места, а также результаты зачисления в вуз победителей и призеров олимпиад школьников, и рассчитывается как их средневзвешенное значение. Более того, в расчетной формуле значения СИКП аналогично формуле (1) присутствует повышающий коэффициент сложности вуза, равный значению 1,10 для технических университетов, значению 1,05 для классических университетов и 1,00 для остальных вузов. Рейтинг вузов по СИКП возглавляют МГУ (123,9 балла), у МФТИ 5-е место, а у МГИМО 6-е место.

Заметим, что показатели СИКП и DmЕ являются корреляционно зависимыми, так как характеризуются по выборке 347 вузов статистически значимыми коэффициентами парных корреляций Пирсона r = 0,177 (уровень значимости p ≈ 0,001) и Спирмена R = 0,209 (уровень значимости p ≈ 0,0001).

Наличие корреляционной связи СИКП и DmЕ позволило использовать факторный анализ для построения двухмерного факторного пространства ПВИ {Ф1, Ф2} и классифицировать Ф1 как фактор качества набора, определенного в значительной степени показателем СИКП, а Ф2 – как фактор динамики качества набора, определенного в значительной степени показателем DmЕ. При этом сами координаты пространства Ф1 и Ф2 являются уже корреляционно независимыми. Далее была проведена кластеризация вузов в {Ф1, Ф2} методом K-средних и построена 8-кластерная модель вузов, согласно λ-критерию Уилкса высоко значимо (на уровне значимости р < 0,000005) различающая 8 кластеров вузов по совокупности {Ф1, Ф2}, а согласно как параметрическому F-критерию, так и ранговому критерию Краскела–Уоллиса высоко значимо (на уровне значимости р < 0,0005) различающая кластеры по каждому фактору.

Затем были рассчитаны факторные средние значения кластеров вузов по каждому фактору, а также для сравнения приведены соответствующие абсолютные кластерные средние по СИКП и DmЕ и их стандартизированные аналоги (табл. 2). В факторном пространстве вычислено также для каждого кластера его евклидово кластерное расстояние по формуле:

.

Таблица 2 – Кластерные средние вузов 2011 г. в абсолютных, стандартизированных и факторных показателях, а также n – число вузов в кластере и RКл – кластерное расстояние

Заметим, что выше перечисленные лидеры российского образования МГИМО, МФТИ и МГУ входят в кластер К7, характеризующийся очень высоким качеством приема и его положительной динамикой.

Согласно как параметрическому апостериорному критерию наименьших значений разности, так и ранговому критерию Краскела–Уоллиса можно выделить для каждого фактора однородные (различающиеся незначимо, то есть на уровне значимости р > 0,10) группы кластеров, расположенные в порядке убывания факторных средних:

• Ф1: {К7}, {К3, К6}, {К2, К5, К8}, {К1, К4}.
• Ф2: {К4}, {К2, К3, К7}, {К1, К5, К6}, {К8}.

Полученные результаты кластеризации вузов наглядно проиллюстрированы графиками кластерных средних в факторных координатах Ф1 и Ф2 (рис. 2), а также диаграммой рассеяния кластерных средних по исходным показателям СИКП и DmЕ (рис. 3).

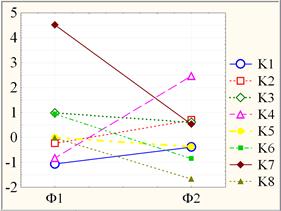
Рис. 2. Графики кластерных средних вузов в факторных координатах Ф1 и Ф2.

Рис. 3. Диаграмма рассеяния кластеров вузов в координатах СИКП и DmЕ .

На основании рис. 2, 3 можно ввести, например, 4 категории уровней качества набора по совокупности показателей СИКП и DmЕ и вычислить с помощью табл. 2 для каждой категории ее евклидово расстояние как среднее арифметическое RКл кластеров, входящих в категорию:

• «низкий», характеризующийся либо средним значением СИКП с отрицательной динамикой DmЕ (К8), либо значением СИКП ниже среднего со слабо положительной динамикой DmЕ (К1) и имеющий = 1,169;
• «средний», характеризующийся либо средним значением СИКП с положительной динамикой DmЕ (К2, К5), либо значением СИКП выше среднего с нулевой динамикой DmЕ (К6) и имеющий = 2,117;
• «высокий», характеризующийся либо значением СИКП выше среднего с положительной динамикой DmЕ (К3), либо значением СИКП ниже среднего с очень сильной положительной динамикой DmЕ (К4) и имеющий = 3,604;
• «лидер», характеризующийся очень высоким качеством приема и его положительной динамикой (К7) и имеющий = 5,993.

Согласно табл. 2 «низкий» уровень качества набора имеют 92 вуза (≈ 26,5%); «средний» – 187 вузов (≈ 53,9%), «высокий» – 61 вуз (≈ 17,6%) и уровень «лидер» – 7 вузов (≈ 2%).

Наконец, для каждой категории уровней качества набора можно вычислить относительное расстояние R = (-min)/(max- min), где max и min наибольшее и наименьшее значения : 1,00 для уровня «лидер»; ≈0,50 для уровня «высокий»; ≈0,20 для уровня «средний» и 0,00 для уровня «низкий»), что позволяет по формуле (2) при определенном Δ (например, Δ = 0,20) вычислить для каждой категории значение коэффициента КВИ : 1,20 для уровня «лидер»; 1,10 для уровня «высокий»; 1,05 для уровня «средний» и 1,00 для уровня «низкий».

Возможна более детальная по ПВИ кластеризация вузов, когда вместо сводного показателя СИКП рассматривается система ПВИ [1]. При этом методика расчета повышающего коэффициента качества набора КВИ аналогична второму варианту кластеризации вузов в двухмерном пространстве показателей вступительных испытаний.

Выводы

1. В рамках модели нормативно-подушевого финансирования вуза с дифференцированными нормативами предложена методика расчета повышающего коэффициента качества набора КВИ на основе кластеризации вузов в пространстве показателей вступительных испытаний.

2. Рассмотрен вариант расчета КВИ на примере одномерного пространства вступительных испытаний – рейтинга вузов по среднему баллу ЕГЭ зачисленных студентов 2012 г.

3. Подробно рассмотрен вариант расчета КВИ на примере двухмерного пространства ПВИ, состоящего из сводного индекса качества приема студентов 2010 г. и динамического показателя разности в средних баллах ЕГЭ среди зачисленных по конкурсу в 2011 и 2010 гг. При этом использован факторный анализ для построения двухмерного факторного пространства, в котором в рамках кластерного анализа построена 8-кластерная модель вузов, выделены группы кластеров вузов, однородных по каждому факторному показателю, построены 4 категории уровней качества набора по совокупности показателей и рассчитаны соответствующие повышающие коэффициенты качества набора.

Работа выполнена в рамках государственного задания «Наука» № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России» по контрактам П691.

Рецензенты:

Трифонов Андрей Юрьевич, д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.

Арефьев Константин Петрович, д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.