Введение
Одним из перспективных направлений в машиностроении является порошковая металлургия. Она обеспечивает создание новых, износостойких и коррозионностойких, жаропрочных, режущих, фрикционных, антифрикционных и многих других материалов с высокими эксплуатационными характеристиками и требуемыми свойствами. Помимо этого, порошковая металлургия открывает широкие возможности по экономии металла и энергии, используемых в производстве материалов, что в свою очередь снижает их себестоимость.
Цель исследования
Создание порошковых материалов с заданными физико-механическими свойствами, с применением комплекса поддержки принятия решений.
Материал и методы исследования
Для исследования используются порошковые низколегированные стали СП100Д1,5. Определяется твердость, предел прочности исходных и термообработанных материалов, а затем проводится моделирование геометрических объектов процесса термической обработки порошковых низколегированных сталей.
Результаты исследования и их обсуждение
Промышленное использование достижений порошковой металлургии часто сталкивается с практически полным отсутствием информационной базы по производству, совершенствованию и использованию изделий порошковой металлургии (ИПМ). Для получения материалов с нужными свойствами требуется проводить весь комплекс длительных и дорогостоящих испытаний, непосредственно в условиях производства [1]. Поэтому, несмотря на очевидные достоинства ИПМ, их применение остается довольно редким. И основными причинами этого являются: недостаточная изученность технологии производства, отсутствие доступных и обоснованных методов принятия конструкторско-технологических решений для совершенствования используемой технологии, низкий уровень автоматизации технологической подготовки производства.
Большинство перечисленных проблем можно решить, используя методы системного анализа и теории управления, в совокупности с современными информационными технологиями [4].
Один из главных методов факторного анализа – метод главных компонент. Он совпадает с методом расчленения ковариационной или корреляционной матрицы на совокупность ортогональных векторов (компонент) или направлений по числу рассматриваемых переменных [3; 4].
В факторном анализе основным предположением является равенство:
![]() , (1)
, (1)
![]() ,
,
где ![]() -я переменная,
-я переменная, ![]() –
– ![]() -й фактор,
-й фактор, ![]() – факторная нагрузка,
– факторная нагрузка, ![]() – количество факторов,
– количество факторов, ![]() – остатки, которые представляют источники отклонений, действующие только на
– остатки, которые представляют источники отклонений, действующие только на ![]() .
.
Вращение подбирается так, чтобы переменные, которые в большей или меньшей степени измеряют некоторые легко опознаваемые стороны, имели бы достаточно высокие нагрузки на один фактор и нулевые или близкие к нулевым на другие факторы [2].
Метод главных компонент можно представить в виде:
![]() , (2)
, (2)
где 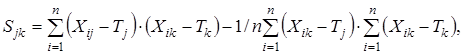
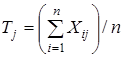
![]() – наблюдения,
– наблюдения,
![]() – переменные.
– переменные.
На следующем этапе проводится оценка парных и комбинированных воздействий, позволяющих определить и выделить особенности комплексного взаимодействия переменных, сначала парные, затем более сложные – комбинированные.
Взаимозависимости парных переменных выявляются при рассмотрении корреляционной таблицы 1, на которой представлены значимые (уровень значимости (р < 0,05) корреляционные функции.
Корреляционные зависимости помогают выявить степень взаимовлияния изменения содержания компонентов или технологических параметров на механические характеристики изделий из порошковых материалов.
Предварительная обработка была осуществлена для матрицы исследования, параметрами – столбиками которой были: 1. Пористость. 2. Тн.з.. 3. Vохл.. 4. Тотп.. 5. Углерод. 6. Медь. 7 σв. 8. НВ.
По знаку корреляционного коэффициента в таблице 1 можно судить о направлении взаимодействия (усиливающее при знаке плюс (+) или ослабляющее при знаке минус (-)), на основании анализа таблицы можно заключить о влиянии переменных в рассматриваемой системе.
Наиболее сильные взаимодействия между процентным содержанием меди и углерода, пористостью и содержанием хрома, пористостью и содержанием меди, пористостью и содержанием никеля.
Можно с уверенность говорить о том, что на пористость содержание углерода влияет меньше, чем содержание меди, никеля.
Технологические режимы влияют следующим образом: температура нагрева под закалку (Тн.з) и скорость охлаждения (Vохл.) оказывают положительное влияние (твердость (НВ) увеличивается), температура отпуска (Тотп) – отрицательная.
Таблица 1 – Результаты корреляционного анализа
|
Параметр |
C |
Cu |
Ni |
Р |
Тн.з |
Vохл. |
Тотп |
НВ |
σв |
|
C |
1,0 |
0,47 |
- |
0,22 |
0,14 |
0,19 |
0,16 |
- |
- |
|
Cu |
0,47 |
1,0 |
0,22 |
0,38 |
0,14 |
0,12 |
- |
- |
- |
|
Ni |
- |
0,22 |
1,0 |
0,35 |
0,15 |
-0,15 |
- |
0,21 |
- |
|
Р |
0,22 |
0,38 |
0,35 |
1,0 |
- |
- |
- |
-0,17 |
-0,711 |
|
Тн.з |
0,14 |
0,14 |
0,15 |
- |
1,0 |
- |
- |
0,21 |
-0,336 |
|
Vохл. |
0,19 |
0,12 |
-0,15 |
- |
- |
1,0 |
- |
0,24 |
- |
|
Тотп |
0,16 |
- |
- |
- |
- |
1,0 |
- |
0,24 |
-0,462 |
|
НВ |
- |
- |
0,21 |
-0,17 |
0,21 |
0,24 |
-0,47 |
1,0 |
0,476 |
|
σв |
- |
- |
- |
-0,711 |
-0,336 |
- |
-0,462 |
0,676 |
1,0 |
Для наглядного представления влияния переменных на механические характеристики использовались графики парного влияния процентного содержания компонентов на твердость образцов из порошковых материалов (рис. 1).
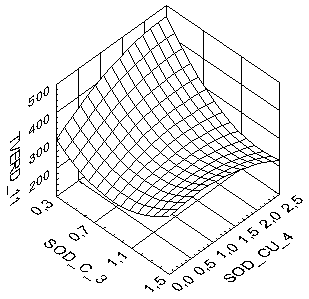
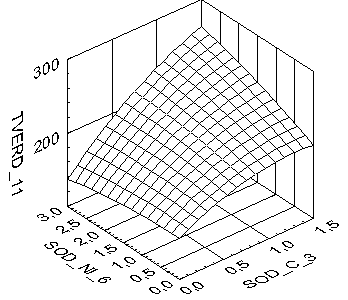
Рис. 1. Зависимость твердости (TVERD) от содержания углерода (SOD_C) и меди (SOD_CU), и никеля (SOD_Ni), в %.
Анализ приведенных графических зависимостей, имеющих седловидный характер, позволяет определить сложное совместное влияние различных составов порошковых материалов и параметров технологических воздействий на контролируемые физические и механические характеристики изделия [5].
На основании этого можно сделать вывод, что графическому анализу должен предшествовать анализ корреляционных коэффициентов. Это помогает избежать ложного, необоснованного толкования графиков.
Для определения групповых обусловленностей проводится факторный анализ.
Все факторы, объединившие в одном факторе параметры исследования, имеют одну природу поведения, то есть они имеют групповую обусловленность. По результатам факторного анализа групповую обусловленность имеют параметры: пористость, предел прочности – объединение в первом факторе; температура нагрева под закалку и скорость охлаждения – объединение во втором факторе; температура отпуска – объединение в третьем факторе.
Рассмотрены параметрические модели прогноза и оценка количественной обусловленности параметров исследования.
Модель для параметра предел прочности (материал СП100Д1,5):
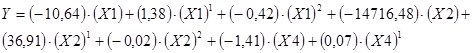 (3)
(3)
где ![]() – пористость (Р),
– пористость (Р), ![]() – температура нагрева под закалку (Тн.з),
– температура нагрева под закалку (Тн.з), ![]() – температура отпуска (Тотп.).
– температура отпуска (Тотп.).
а) 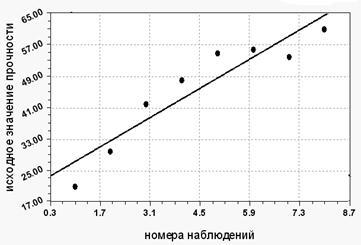 б)
б) 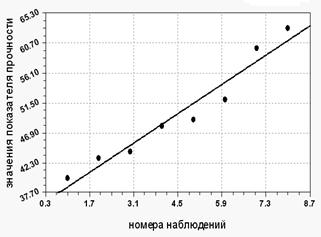
Рис. 2. Графики исходного (а) и модельного (б) изменения σв.
Таблица 2 – Характеристики модели для параметра предел прочности
|
Характеристики модели |
Значения |
|
Коэффициент детерминации |
0,93 |
|
Средняя абсолютная ошибка |
5,37 |
|
Средняя ошибка в процентах |
9,97 |
Модель для параметра твердость (материал СП100Д1,5):
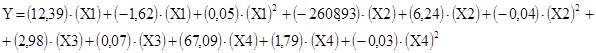 (4)
(4)
где ![]() – пористость (Р),
– пористость (Р), ![]() – температура нагрева под закалку (Тн.з),
– температура нагрева под закалку (Тн.з), ![]() – скорость охлаждения (Vохл.),
– скорость охлаждения (Vохл.), ![]() – температура отпуска (Тотп.).
– температура отпуска (Тотп.).
а) 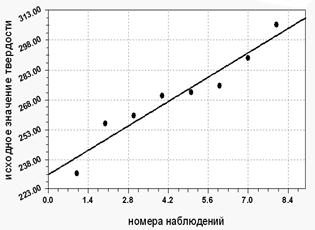 б)
б) 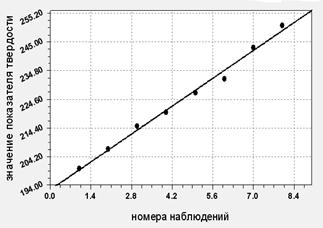
Рис. 3. График исходного (а) и модельного (б) изменения НВ.
Таблица 4 – Характеристики модели для параметра твердость
|
Характеристики модели |
Значения |
|
Коэффициент детерминации |
0,71 |
|
Средняя абсолютная ошибка |
24,51 |
|
Средняя ошибка в процентах |
10,13 |
Характер количественной обусловленности, полученной по моделям, построенным методом Брандона Д. и методом наименьших квадратов, различен из-за процедуры элиминирования в методе Брандона.
Выводы
1. Для параметров матриц исследования определены основные статистические характеристики, доверительные интервалы для оценки математических ожиданий.
2. Построены корреляционные матрицы и сделана по ним оценка парных обусловленностей параметров исследования.
3. По результатам объединений по факторам находились базовые параметры.
4. Из двух моделей, построенных методом наименьших квадратов и методом Брандона Д., для параметрического прогноза и оптимизации выбиралась модель с минимальной средней абсолютной ошибкой.
5. Для оптимальных значений параметров были определены по параметрическим моделям прогноза значения остальных параметров исследования.
Рецензенты:
Богодухов Станислав Иванович д.т.н., профессор, зав. кафедрой материаловедения и технологии материалов Аэрокосмического института Оренбургского государственного университета, г. Оренбург.
Сердюк Анатолий Иванович д.т.н., профессор, директор Аэрокосмического института Оренбургского государственного университета, г. Оренбург.



