Введение
Известные автобалансирующие устройства (АБУ) достаточно эффективно уменьшают режимное изменение дисбаланса ротора. Однако такая результативность достигается за счет использования тяжелой жидкости (ртути) в качестве корректирующей массы [8]. При разработке машин и приборов стремятся избегать использования высокотоксичных веществ. Имеющиеся нетоксичные жидкости обладают плотностью не более 2 г/см3, поэтому использование их в качестве корректирующей массы в жидкостных АБУ, вместо ртути, ведет к снижению эффективности автоматической балансировки ротора [7]. Именно из-за недостаточной эффективности жидкостных АБУ, обусловленной малой плотностью жидкости, факторы, влияющие на точность балансировки, были слабо освещены. На кафедре ТПМ ТПУ было разработано устройство [1], позволяющее многократно повышать эффективность автоматической балансировки роторов с помощью жидкостных АБУ. В связи с этим возникла необходимость исследования различных факторов, которые влияют на точность балансировки.
Материал и методы исследования
В большинстве работ [3; 7; 9], посвященных исследованию балансировки ротора жидкостными АБУ, используется модель, содержащая обойму, жестко закрепляемую на гибком валу; полость в обойме частично заполняется жидкостью, т.е. обойма играет роль резервуара. В некоторых реальных машинах ротор жесткий, а корпус упруго связан с основанием. Динамику такой машины точнее описывает модель ротора, содержащая резервуар-обойму, закрепляемую на жестком валу, который имеет возможность вращения в подшипниках [5; 6]. Подшипники идеальные (без люфта) установлены в корпусе, который упруго связан с основанием.
Результаты исследования и их обсуждение
Покажем влияние различных факторов на точность балансировки – это необходимо для пояснения дальнейших исследований.
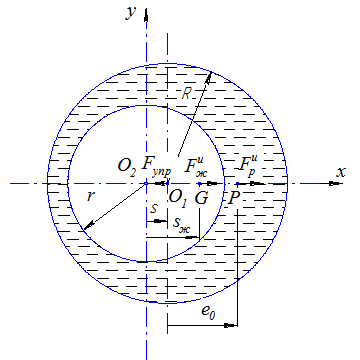
Рис. 1. Схема сил в жидкостном АБУ.
По первому варианту модели при вращении ротора с постоянной частотой ω=const и сдвиг фаз γ=0 в зарезонансной области отражен на рис. 1. Вал ротора прогибается таким образом, что вся система: резервуар, жидкость – осуществляет вращение вокруг неподвижной оси z (в проекции точка О2), проходящей через центры поперечных сечений цапф вала ротора. При этом свободная поверхность жидкости в обойме принимает форму параболоида вращения, который обычно [4; 7; 10] аппроксимируется цилиндром. Силы, действующие на резервуар, удовлетворяют уравнению, составленному по методу кинетостатики:
или в проекциях на ось x:
, (1)
где: Fупр=cs – сила упругости гибкого невесомого вала в радиальном направлении;
– сила инерции ротора, приложенная к его центру масс (точка P);
– сила инерции жидкости, приложенная к ее центру масс;
c – радиальная жесткость вала в плоскости камеры;
s – прогиб вала в плоскости резервуара;
m – масса ротора с резервуаром;
e0 – начальный дисбаланс ротора;
– масса жидкости;
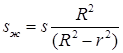– расстояние от оси вращения ротора до центра масс жидкости;
ω – частота вращения ротора;
ρ, r – плотность жидкости и радиус ее свободной поверхности;
h, R – высота и радиус внутренней поверхности резервуара.
Из уравнения (1) получается известное выражение для прогиба вала ротора в плоскости коррекции [2], а также выражение (4) при отсутствии внешнего трения χ=0:
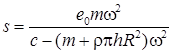. (2)
Анализ этого уравнения показывает, что прогиб вала, а вместе с ним и динамические нагрузки в опорах ротора тем больше, чем начальный дисбаланс ротора и чем ближе частота вращения ротора к резонансной частоте, определяемой выражением:
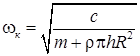. (3)
Отсюда видно, что резонансная частота зависит от радиальной жесткости вала, массы ротора и параметров жидкостного автобалансирующего устройства ρ, h, R.
Уравнения (2) и (3), критическая частота ωк и прогиб вала s не зависят от радиуса r2 свободной поверхности жидкости, от которого зависит значение объема жидкости в обойме, а соответственно и ее массы. Следовательно, жидкости в обойме должно быть столько, чтобы ее свободная поверхность не пересекалась с внутренней цилиндрической частью поверхности камеры, запишем это условие:
. (4)
Это неравенство является условием достаточности жидкости. Получается парадоксальный результат: масса жидкости в резервуаре зависит от радиуса свободной поверхности жидкости, а прогиб вала s, как видно из выражения (2), от радиуса свободной поверхности жидкости не зависит при выполнении условия (4) достаточности жидкости. Следовательно, прогиб вала от массы жидкости не зависит при выполнении условия ее достаточности. Это может быть объяснено следующим образом. При выполнении условия (4) имеется часть 1 жидкости (рис. 2), заключенная между свободной поверхностью 5 жидкости и цилиндрической поверхностью 6, касающейся поверхности 2 резервуара и имеющей ось, совпадающую с осью вращения ротора. Эта часть жидкости не участвует в процессе балансировки, так как ее центр масс совпадает с осью вращения ротора, и эта часть жидкости уравновешивает саму себя.
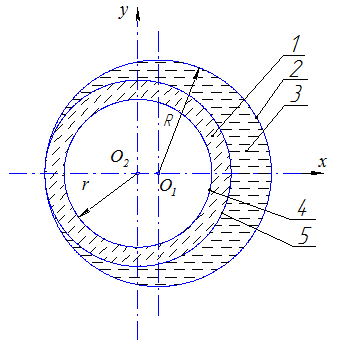
Рис. 2. Схема, поясняющая достаточность жидкости в обойме:
1 – жидкость, не участвующая в балансировке; 2 – поверхность резервуара; 3 – жидкость, участвующая в балансировке; 4 – свободная поверхность жидкости; 5 – поверхность, определяющая условие достаточности жидкости.
При невыполнении условия (4) свободная поверхность жидкости прерывается поверхностью резервуара. В этом случае прогиб s1 вала определяется уравнением:
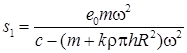. (5)
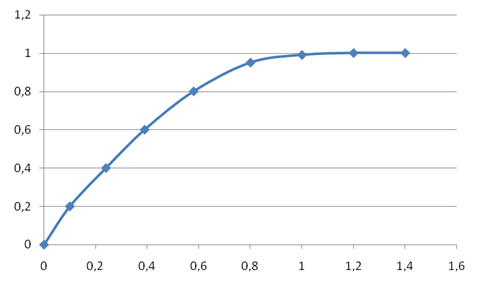
Это уравнение отличается от уравнения (2) наличием переводного коэффициента k , который при невыполнении условия достаточности жидкости находится в функциональной зависимости от массы жидкости. Точное выражение для этой зависимости довольно громоздко по форме, поэтому на рис. 3 приведена диаграмма зависимости переводного коэффициента от отношения mж/m0, где m0 – граничное значение массы жидкости, удовлетворяющее условию достаточности жидкости. Это значение определяется формулой:
. Таким образом, амплитуда колебаний ротора оказывается связанной с массой жидкости в камере, но только при выполнении условия достаточности жидкости.
k
mж/ m0
Рис. 3. Диаграмма зависимости переводного коэффициента.
Аналогично и критическая частота вращения ротора при невыполнении условия (4) оказывается в зависимости от массы жидкости в камере. Эта частота определяется выражением:
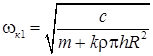. (6)
При приближении частоты вращения ротора к критической частоте, определяемой соотношением (8), должно наблюдаться возрастание амплитуды колебаний ротора s.
Кроме найденного значения прогиба ротора, которое может служить критерием оценки качества балансировки, так как оно определяет уровень вредного воздействия вибрации на человека, в ряде случаев [3] качество балансировки оценивают по точности балансировки, выраженной через остаточный удельный дисбаланс, который равен эксцентриситету массы ротора. Поэтому определим эксцентриситет массы системы «ротор – жидкость» относительно оси обоймы (точка O1 на рис. 1) по выражению:
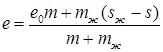, (7)
откуда при частоте вращения ротора, гораздо большей критической, получается удельный дисбаланс ротора:
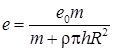. (8)
Используя выражения (2) и (9), определим эффективность снижения прогиба вала и дисбаланса ротора:
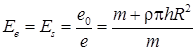, (9)
где: 
– эффективность снижения прогиба вала ротора (амплитуды колебаний ротора) при частоте вращения ротора, гораздо больше критической;
– эффективность снижения дисбаланса ротора при той же частоте вращения ротора, т.е. эффективность автоматической балансировки.
Выводы
По полученным результатам можно сделать следующие выводы: амплитуда колебаний на закритических частотах будет тем меньше, чем больше параметры жидкостного автобалансирующего устройства – высота и радиус внутренней поверхности резервуара, а также плотность жидкости. Эффективность автоматической балансировки тем выше, чем больше параметры жидкостного АБУ. При выполнении условия достаточности жидкости в обойме амплитуда колебаний ротора оказывается независимой от массы жидкости в резервуаре. Критическая частота вращения ротора не зависит от объема жидкости в обойме при выполнении условия ее достаточности.
Рецензенты:
Тарасов Сергей Юльевич, д.ф.-м.н., с.н.с. ИФПМ СО РАН, г. Томск.
Пушкарев Александр Иванович, д.ф.-м.н., сотрудник ООО «Инженерно-физический центр», г. Томск.