Введение
Высокоскоростное (сверхзвуковое) газопламенное напыление (HVOF) является сравнительно недавним дополнением к семейству процессов газотермического напыления. Данная методика по праву считается наиболее современной из технологий напыления. В странах Европы и Северной Америки HVOF практически вытеснило гальванику и методы вакуумного напыления во многих отраслях. Из-за малой скорости частиц при газоплазменном напылении поверхность частиц успевает окислиться, что приводит к низкой плотности формирования покрытий. Увеличение скорости частиц при меньшей их температуре позволило снизить уровень окисленности частиц и повысить плотность порошкового покрытия. В порошковых распылителях HVOF первого и второго поколений использовалось цилиндрическое сопло, тогда как в третьем поколении используются расширяющиеся профильные сопла Лаваля. Такой подход позволяет скорости потока газа превышать 2000м/с, а скорости частиц порошка 800м/с. При HVOF методике достигается высокая адгезия, а пористость покрытия не превышает 1% [8].
В последнее время получено много результатов по упругим и прочностным свойствам многослойных покрытий, полученных методом сверхзвукового газопламенного напыления [2-4]. Но основная часть работ по исследованию покрытий, полученных методом HVOF, посвящена исследованию их напряженно-деформируемого состояния при статических нагрузках. Анализ же деформирования и разрушения подобных сред при динамических нагрузках сложен и требует, как правило, трехмерного подхода и адекватных моделей поведения не только каждого отдельного слоя покрытия, но и подложки.
В данной работе исследуется поведение многослойного покрытия со стальной подложкой при динамическом нагружении конструкции ударником при различных скоростях взаимодействия. Задача решалась численно, методом конечных элементов с использованием явной конечно-разностной схемы Г. Джонсона [5].
Основные уравнения математической модели
Система уравнений, описывающих нестационарные адиабатные движения сжимаемой среды в декартовой системе координат ![]() , включает уравнения неразрывности, движения и энергии:
, включает уравнения неразрывности, движения и энергии:
![]() ,
,
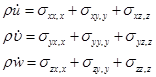 ,
,
![]() .
.
Здесь ![]() – плотность среды;
– плотность среды; ![]() – вектор скорости;
– вектор скорости; ![]() ,
, ![]() ,
, ![]() – компоненты вектора скорости по осям
– компоненты вектора скорости по осям ![]() соответственно;
соответственно; ![]() – компоненты симметричного тензора напряжений;
– компоненты симметричного тензора напряжений; ![]() – удельная внутренняя энергия;
– удельная внутренняя энергия; ![]() – компоненты симметричного тензора скоростей деформаций. Точка над символом обозначает производную по времени, запятая после символа – производную по соответствующей координате.
– компоненты симметричного тензора скоростей деформаций. Точка над символом обозначает производную по времени, запятая после символа – производную по соответствующей координате.
Поведение стального изотропного цилиндра, являющегося ударником, при высокоскоростном ударе описывается упругопластической средой, в которой связь между компонентами тензора скоростей деформации и компонентами девиатора напряжений определяется соотношениями Прандтля–Рейса [6]:
![]() ,
,
где ![]() ,
, ![]() — модуль сдвига,
— модуль сдвига, ![]() — параметр, который определяется с помощью условия Мизеса:
— параметр, который определяется с помощью условия Мизеса: ![]() , при этом
, при этом ![]() — динамический предел текучести (при упругой деформации
— динамический предел текучести (при упругой деформации ![]() , а при пластической
, а при пластической ![]() ). Шаровая часть тензора напряжений (давление) рассчитывается по уравнению Ми–Грюнайзена как функция удельной внутренней энергии
). Шаровая часть тензора напряжений (давление) рассчитывается по уравнению Ми–Грюнайзена как функция удельной внутренней энергии ![]() и плотности
и плотности ![]() :
:
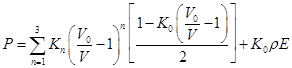 ,
,
где ![]() — константы материала,
— константы материала, ![]() и
и ![]() — начальный и текущий удельные объёмы материала соответственно. Данной моделью также описывается поведения стальной подложки и покрытия NiAl.
— начальный и текущий удельные объёмы материала соответственно. Данной моделью также описывается поведения стальной подложки и покрытия NiAl.
Поведение материала покрытия из WC-Co не выходит за рамки упруго-хрупкой модели. Компоненты тензора напряжений в материале преграды до момента разрушения удовлетворяют соотношениям обобщенного закона Гука, записанного в терминах скоростей деформаций:
![]()
В качестве критерия разрушения материала подложки используется критерий Хоффмана. Данный критерий позволяет использовать различные прочностные характеристики материала на растяжение и сжатие, и, выраженный через скалярные функции компонент тензора напряжений, имеет вид:
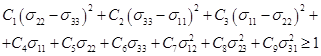 ,
,
где ![]() – постоянные материала.
– постоянные материала.
Предполагается, что разрушение материала покрытия в условиях интенсивных динамических нагрузок происходит следующим образом: если критерий прочности (1) нарушается в условиях сжатия (![]() ), то материал ведет себя как жидкость, при этом материал сохраняет прочность только на сжатие, а тензор напряжений становится в этом случае шаровым (
), то материал ведет себя как жидкость, при этом материал сохраняет прочность только на сжатие, а тензор напряжений становится в этом случае шаровым (![]() ); если критерий (1) нарушается в условиях растяжения (
); если критерий (1) нарушается в условиях растяжения (![]() ), то материал считается полностью разрушенным и компоненты тензора напряжений полагаются равными нулю (
), то материал считается полностью разрушенным и компоненты тензора напряжений полагаются равными нулю (![]() ).
).
Как уже отмечалось ранее, численное моделирование проводится методом конечных элементов в трехмерной постановке. Расчет контактных границ осуществляется по алгоритму, предложенному в работе [6], основанному на применении законов сохранения количества движения и момента количества движения к узлам контактных поверхностей.
Для проверки адекватности, как моделей, так и конечно-разностной схемы был сделан ряд сравнений численных и экспериментальных данных, который показал их удовлетворительное согласование [7]. Также исследована сходимость численного решения, которая послужила основой для дискретизации областей конечными элементами. При численном моделировании максимальное количество конечных элементов (тетраэдров), на которые далее разбивается расчетная область, составляет 2,35·106, при этом количество узлов равняется 4,3·105 (рис.1). Шаг сетки отдельных материалов конструкции был выбран таким образом, чтобы масса всех узлов расчетной области была приблизительно равной. Данное условие значительно повышает точность численного решения. В зависимости от начальной скорости и наличия многослойного покрытия на расчет соответствующего начальным данным варианта задачи требуется приблизительно 1,3·104 временных шагов.
Постановка задачи
В работе рассматривается задача влияния двухслойного покрытия на поведение стальной подложки при динамическом нагружении. Стальная подложка из стали марки 316L (0,03% C, 1% Si, 2% Mn, 0,045% P, 0,03% S, 16–18% Cr, 2–3% Mo и 10–14% Ni) толщиной 1,5мм имеет двухслойное покрытие, нанесенное методом HVOF (сверхзвуковое газоплазменное напыление). Первый слой из сплава NiAl (95% Ni и 5% Al), второй слой содержит 87% WC и 13% Co [9]. Данная конструкция нагружается стальным компактным цилиндрическим ударником из стали марки Ст3. Начальная скорость нормального удара составляет 200 и 400м/с. Толщина первого слоя варьируется от 105 до 355нм, второго – соответственно от 350 до 100нм таким образом, чтобы суммарная толщина всей конструкции оставалась постоянной. Для удобства введем коэффициент ![]() , где
, где ![]() – толщина соответствующего слоя. Механические характеристики материалов представлены в табл. 1.
– толщина соответствующего слоя. Механические характеристики материалов представлены в табл. 1.
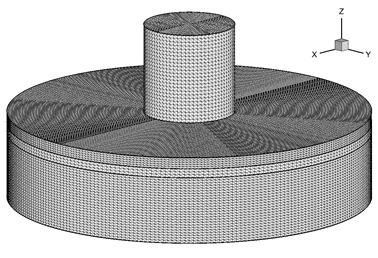
Рис. 1 Схема взаимодействия ударника с мишенью. Расчетная сетка.
Начальный момент времени.
Табл. 1.
|
|
Сталь 3 |
316L |
NiAl |
WC-Co |
|
Плотность, кг/м3 |
7850 |
8031 |
5900 |
13900 |
|
Модуль Юнга, ГПа |
204 |
200,38 |
169 |
398 |
|
Коэффициент Пуассона |
0,3 |
0,29 |
0,32 |
0,25 |
|
Предел текучести, МПа |
1010 |
262 |
1453 |
– |
|
Предел прочности, МПа |
– |
– |
– |
4500 |
![]() .
.
Здесь ![]() – единичный вектор нормали к поверхности в рассматриваемой точке;
– единичный вектор нормали к поверхности в рассматриваемой точке; ![]() и
и ![]() – единичные векторы, касательные к поверхности в этой точке;
– единичные векторы, касательные к поверхности в этой точке; ![]() — вектор силы на площадке с нормалью
— вектор силы на площадке с нормалью ![]() ;
; ![]() – вектор скорости. Нижние индексы у векторов
– вектор скорости. Нижние индексы у векторов ![]() и
и ![]() обозначают проекции на соответствующие векторы базиса; знак «+» указывает на соответствие значений параметров материала верхней границе контактной поверхности, знак «–» – нижней границе.
обозначают проекции на соответствующие векторы базиса; знак «+» указывает на соответствие значений параметров материала верхней границе контактной поверхности, знак «–» – нижней границе.
Обсуждение результатов
Одним из важнейших показателей является амплитуда волн, возникающих в материале преграды после взаимодействия с ударником. На рис. 2 представлены зависимости значений напряжений sz в центральной точке продольной оси стальной подложки для различных значений коэффициента K. Видно, что для случая начальной скорости 200м/с амплитуда как волны сжатия, так и волны разгрузки минимальна для случаев K=0,28 и К=0,49 (максимальная разность составляет 81%), в то время как для случая начальной скорости 400м/с амплитуда для К=0,28 оказывается максимальной, постепенно уменьшаясь с возрастанием коэффициента К и достигая разности в 23,5%.
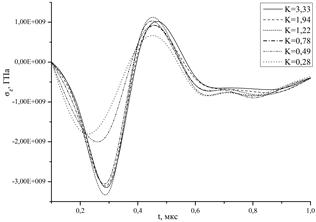
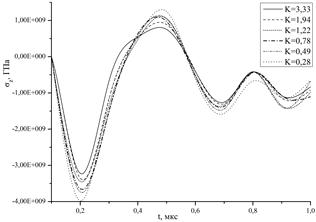
Рис. 2. Зависимость амплитуды напряжений sz от коэффициента К.
Начальная скорость 200м/с (слева) и 400м/с (справа).
На рис. 3 представлено распределение напряжений sz в момент времени ![]() мкс для случая начальной скорости 200м/с. Видно, что картина распределения в данной случае меняется и является менее равномерной, и концентраторы сжимающих напряжений сосредоточены вблизи центральной оси преграды, а также в области, располагающей в месте контакта преграды и боковой поверхности ударника. Остаточная скорость центра масс ударника для случая
мкс для случая начальной скорости 200м/с. Видно, что картина распределения в данной случае меняется и является менее равномерной, и концентраторы сжимающих напряжений сосредоточены вблизи центральной оси преграды, а также в области, располагающей в месте контакта преграды и боковой поверхности ударника. Остаточная скорость центра масс ударника для случая ![]() м/с находится в пределах 39,2м/с (
м/с находится в пределах 39,2м/с (![]() ) и 43,2м/с (
) и 43,2м/с (![]() ).
).
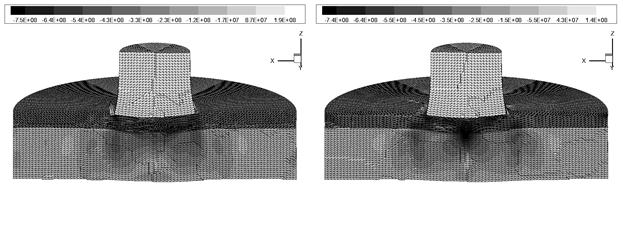
Рис. 3. Распределение напряжений sz по преграде в плоскости ![]() для случаев
для случаев ![]() (слева) и
(слева) и ![]() (справа) при
(справа) при ![]() мкс.
мкс. ![]() м/с.
м/с.
На рис. 4 представлено распределение напряжений sz в момент времени ![]() мкс для случая начальной скорости 400м/с. Видно, что картина распределения напряжений в материале подложки иная и концентрация напряжений равномерно сосредоточена в области пятна контакта.
мкс для случая начальной скорости 400м/с. Видно, что картина распределения напряжений в материале подложки иная и концентрация напряжений равномерно сосредоточена в области пятна контакта.
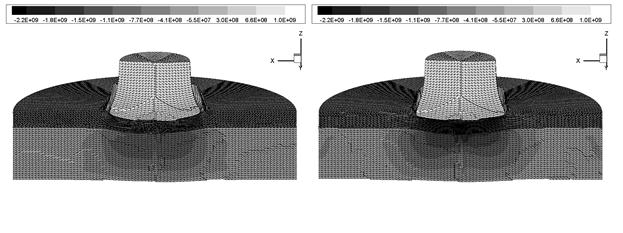
Рис. 4. Распределение напряжений sz по преграде в плоскости ![]() для случаев
для случаев ![]() (слева) и
(слева) и ![]() (справа) при
(справа) при ![]() мкс.
мкс. ![]() м/с.
м/с.
Заключение
В работе проведен сравнительный анализ проникающей способности ударника в стальную монолитную преграду и преграду с многослойным NiAl - WC-Co покрытием. Исследования показали, что наличие высокопрочного слоя, полученного методом HVOF, повышает сопротивление разрушению конструкции при ударном нагружении. Повышение прочности не пропорционально соотношению объемов покрытия и преграды, а достигается за счет изменения характера развития волновых процессов и связанного с этим снижения уровня растягивающих напряжений в зоне вероятного откола. В результате происходит более интенсивное торможение и деформирование ударника на начальной стадии процесса, что приводит к уменьшению его проникающей способности. Данный эффект наиболее ярко выражен для низких и средних скоростей ударника.
Исследование выполнено в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы (Государственное соглашение № 14.A18.21.2108 по обобщенной теме «Современные методы исследования микроструктуры и механических свойств перспективных материалов») на оборудовании Центра коллективного пользования «Диагностика структуры и свойств наноматериалов» НИУ «БелГУ».
Рецензенты:
Кайбышев Рустам Оскарович, д.ф.м.н., профессор кафедры «Материаловедения и нанотехнологий» ФГАО ВПО «Белгородский государственный национальный исследовательский университет», руководитель лаборатории механических свойств наноструктурных и жаропрочных материалов ФГАО ВПО «Белгородский государственный национальный исследовательский университет», г.Белгород.
Иванов Олег Николаевич, д.ф.-м.н., директор Центра коллективного пользования «Диагностика структуры и свойств наноматериалов» ФГАО ВПО «Белгородский государственный национальный исследовательский университет», г.Белгород.



