Введение
Задачи синтеза управляющих воздействий в неуравновешенном конечном состоянии исследовались многими авторами [2–5], что объясняется развитием вычислительных и измерительных средств контроля и управления техническими объектами. При этом в качестве исследуемой модели выступал математический маятник, в определенной мере отражающий разнообразные механические системы – от ориентации космических аппаратов до поведения различных манипуляционных роботов.
Известно большое число методов, обеспечивающих получение оригинальных алгоритмов управления, как правило, использующих допущения о величине отклонения от положения равновесия и форме математической модели системы управления [3 – 5, 15]. В частности, применение идеи декомпозиции приводит к управлениям близким к оптимальным, если величины возмущений и нелинейностей в системе оказываются малыми [15].
Синтез управления нелинейной динамической системой может быть осуществлен на основе результатов предложенных в [14] или в [11], которые получены с привлечением концепции обратных задач динамики. Однако в первом случае обратная связь определена с точностью до неизвестной функции, что ограничивает практическую возможность её использования. Во втором получается динамическая система, чьи характеристики «почти идентичны динамическим характеристикам эталонных моделей» [11]. Таким образом, проблема управления нелинейными неустойчивыми динамическими системами остается актуальной.
В данной работе предлагается универсальный подход к синтезу оптимальных управлений нелинейной динамической системой, базирующийся на теории объединенного принципа максимума [1, 7 – 10]. Полученные решения демонстрируют нетривиальную связь между методом ОПМ и принципом максимума Л. С. Понтрягина [13]. Результаты математического моделирования показывают, что в положениях неустойчивого равновесия он обеспечивает статическую уравновешенность внешних опрокидывающих и управляющих сил, что трудно осуществить получившим распространение релейным управлением [6, 15].
1. Метод объединенного принципа максимума. Движение управляемой системы подчиняется принципу Гамильтона – Остроградского на конечном промежутке времени 
[2]
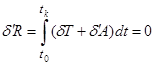, (1)
;
мерой качества управляемого процесса выбран целевой функционал
, (2)
где 
– обобщенные координаты и скорости; 
– определенно-положительная функция;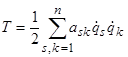 
– кинетическая энергия; 
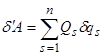– элементарная работа обобщенных сил, зависящих от управлений, 
. Управления выбираются из некоторой замкнутой области 
, 
– число искомых параметров управления. В качестве функций управления может назначаться и обобщенная сила 
.
Из принципа (1) следуют уравнения Лагранжа второго рода
. (3)
Задача состоит в построении таких допустимых управлений 
или , которые переводят систему (3) из начального состояния 
в конечное 
, а целевой функционал (2) принимает при этом минимальное значение.
Условие ОПМ является результатом поиска условия минимума расширенного целевого функционала [1, 6 – 10]
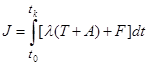, (4)
где 
– неопределенный множитель Лагранжа.
Теорема. Для того чтобы обобщенная сила 
и соответствующая ей траектория 
доставляли минимум расширенному функционалу (2.4), необходимо выполнить условия максимума для обобщенной мощности
, (5)
при этом 
, а на концах траектории 
выполняются условия трансверсальности для функции Гамильтона – Остроградского и обобщенного кинетического потенциала
; (6)
, (7)
где 
– фиктивная обобщенная сила, зависящая от формы задания целевого функционала. Ее доказательство приведено в [10].
Из (5) следует, что значения , соответствующие минимуму (2), определяются выражением
, (8)
где 
– синтезирующая функция. Она определяется из анализа условия трансверсальности (6) на поверхности переключения управления (8) [1, 9]. Тогда для кусочно-постоянных управлений справедливо:
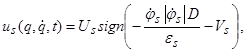
, (9)
или в форме принципа максимума Л. С. Понтрягина:
, (10)
а для кусочно-непрерывных управлений:
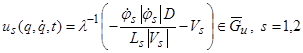, (11)
где 
– независимые множители Лагранжа, 
– константа, определяющая диаметр эллипса в фазовом пространстве, 
– константа, зависящая от формы линии переключения, 
– допустимое управление [9]. Таким образом, в классе кусочно-постоянных функций решения ОПМ и принципа максимума Л. С. Понтрягина совпадают.
2. Синтез управления нелинейной системой в положении неустойчивого равновесия. Рассматривается двойной маятник. Уравнения Лагранжа второго рода (3) принимают следующий вид:
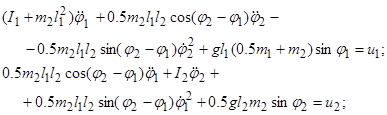(12)
где 
и 
– моменты инерции стержней ОА и АВ относительно осей, перпендикулярных плоскости Оху и проходящих через шарниры О и А (рисунок 1); 
, 
– их массы, а 
и 
– длины; 
,
– углы отклонения стержней ОА и АВ от вертикали; 
– ускорение свободного падения.
Ставится задача: перевести динамическую систему (12) из произвольного начального положения 
в произвольное неуравновешенное состояние 
и удерживать ее там, если заданы ограничения на управления: 
.
Выбрана следующая форма целевого функционала (2):
. (13)
Оптимальные решения для кусочно-постоянных и кусочно-непрерывных управлений получены с использованием формул (9), (10), (11), в которых для (9) оптимальными являются параметры: 
, 
, 
, 
, 
, 
, 
; для (10): 
, 
; для (11): 
, 
, 
.
Результаты математического моделирования представлены на рисунке 1; расчетные значения целевого функционала (13) следующие: для (9) 
; для (10) 
; а для (11) 
.
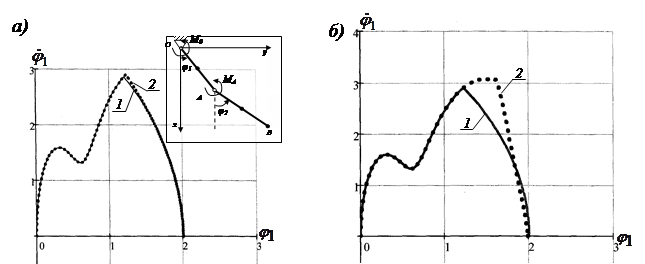
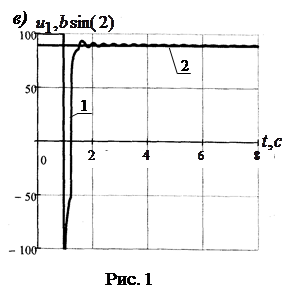
Результаты математического моделирования показывают, что синтезированные управления обеспечивают статическую уравновешенность внешних опрокидывающих и управляющих сил [14].
Выводы
Новый метод синтеза оптимального управления – объединенный принцип максимума – обладает универсальностью и простотой применения в сравнении с методом Л. С. Понтрягина, который предполагает поиск и анализ решения краевой задачи с целью определения явной формы обратной связи, что во многих практически важных случаях не может быть реализовано. Универсальность метода определяется возможностью использования аналитической формы выражения оптимального управления при решении задачи синтеза для любых динамических систем, удовлетворяющих принципу Гамильтона – Остроградского и записанных в виде дифференциальных уравнений Лагранжа второго рода.
Синтезированные управления обеспечивают высокую эффективность решения классической тестовой задачи механики и теории управления, которая понимается в смысле простоты полученных аналитических выражений, небольшого объема вычислительных затрат.
Исследование проведено при поддержке Министерства образования и науки Российской Федерации, соглашение 14В37.21.2067
Рецензенты:
Звездина Марина Юрьевна, доктор физико-математических наук, доцент, заведующая кафедрой "Радиоэлектроника", Минобрнауки России, Ростовский технологический институт сервиса и туризма (филиал) Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Южно-Российский государственный университет экономики и сервиса», г. Ростов-на-Дону.
Риполь-Сарагосси Татьяна Леонидовна, доктор технических наук, профессор, заместитель директора по дополнительному образованию, Минобрнауки России, Филиал государственного образовательного учреждения высшего профессионального образования "Московский государственный университет технологий и управления", г. Ростов-на-Дону.