В последние годы за рубежом в строительстве жилых и общественных зданий широко используется комбинированная технология строительства (КТС), которая заключается в сочетании несущего железобетонного каркаса и ограждающих стеновых панелей на деревянном каркасе. Началось освоение КТС и в нашей стране (жилой комплекс «Славянка» в г. Пушкин, СПб). В данном случае стеновые панели на деревянном каркасе устанавливались на железобетонные перекрытия здания и входили в состав многослойной ограждающей конструкции, включающей наружное утепление и навесную фасадную систему с воздушным зазором и облицовкой из керамогранитных плит [6]. В качестве обшивок панели были применены как наиболее рациональный вариант с точки зрения эксплуатационных свойств, технологичности и экономичности при изготовлении, цементно-стружечные плиты (ЦСП) [5], которые крепились к каркасу при помощи металлических оцинкованных скоб.
Поскольку стеновая панель на деревянном каркасе при КТС не является несущей, то для оценки ее жесткости достаточно экспериментально определить прогиб в направлении, перпендикулярном фронтальной плоскости панели, от ветровой нагрузки и напряжения, возникающие в элементах каркаса и обшивках. Соединение при помощи металлических скоб обладает некоторой величиной податливости, что сказывается на общей жесткости панели. Соответственно, расчет несущей способности составного изгибаемого элемента - стеновой панели на деревянном каркасе - следует вести с введением в него коэффициентов податливости, которые определяются в каждом случае в зависимости от параметров панели.
Целью данной работы явилось исследование возможности применения метода конечных элементов для расчета несущей способности стеновых панелей на деревянном каркасе по I и II группам предельных состояний с учетом совместной работы каркаса и обшивки на податливых связях.Для этого возникла необходимость проведения комплекса исследований, включающего экспериментальное определение несущей способности соединения при помощи металлических скоб, расчет рационального шага расстановки скоб (при заданной нагрузке), экспериментальное определение прогиба полномасштабной модели стеновой панели от различных знакопеременных ветровых нагрузок, расчет коэффициентов податливости соединения листов обшивки и элементов каркаса и на заключительном этапе - имитационное моделирование процесса ветрового воздействия при помощи метода конечных элементов в проектно-вычислительном ПК SCAD.
Вначале были определены ветровые нагрузки согласно [3]. Рассматривался несколько упрощенный случай прямоугольного в плане здания с протяженностью фасада, большей, чем максимальная высота. При этом были выбраны два уровня наибольшей допустимой высоты здания - 28 м (II степень огнестойкости, класс конструктивной пожарной опасности С1) и 75 м (I степень огнестойкости, класс конструктивной пожарной опасности С1). Т.к. для приторцовой зоны фасада и для его центральной части значения ветровых нагрузок отличны друг от друга, то получилось четыре расчетных случая (два уровня высоты и две зоны расположения панели на фасаде). Расчетные ветровые нагрузки, воздействующие на стеновую панель, приведены в табл. 1 (II ветровой район, тип местности В, г. Санкт-Петербург).
Таблица 1. Ветровые давления, действующие на стеновую панель
|
Ветровое давление |
Высота здания, зона расположения панели на фасаде |
|||
|
Отметка +28,0 м |
Отметка +75,0 м |
|||
|
Центральная |
Приторцовая |
Центральная |
Приторцовая |
|
|
Положительноеw+p, кПа |
0,74 |
0,74 |
0,97 |
0,97 |
|
Отрицательноеw_p, кПа |
- 0,69 |
- 1,26 |
- 0,91 |
- 1,67 |
Для определения несущей способности соединения деревянных элементов каркаса и обшивок панели из ЦСП при помощи металлических скоб были проведены испытания с последующей обработкой данных согласно [7] и [8]. Полученное значение несущей способности одной скобы - 1,03 кН.


Рис. 1. Определение несущей способности соединения скобой; слева - на сдвиг, справа - на выдергивание
Затем, для заданных ветровых нагрузок (табл. 1) был определен рациональный шаг расстановки крепежных скоб. Для этого при помощи метода конечных элементов в ПК SCAD была определены усилия на погонный метр шва соединения обшивки и каркаса при ветровых воздействиях. Для полной передачи усилий упругие связи заменялись жесткими, расставленными с шагом 0,1 м. Усредненное значение эквивалентного линейно-распределенного усилия составило 4,06 кН/м, а усилие вырыва скоб - 0,45 кН/м. Таким образом, на погонный метр вертикальной стойки каркаса требуется 3,9 скоб для крепления листов обшивки из ЦСП. Однако ввиду неравномерности распределения напряжений и для обеспечения запаса прочности, следует принимать 5 скоб на погонный метр, т.е. рациональным шагом расстановки скоб при исследованных нагрузках является 0,2 м.
После определения рационального шага расстановки скоб была создана полномасштабная модель стеновой панели, и проведены ее испытания на прогиб при воздействии различных знакопеременных ветровых нагрузок (рис. 2). При этом условия закрепления панели полностью соответствовали существующим конструктивным решениям. Полученные средние прогибы центра тяжести панели по экспериментальным данным приведены в табл. 2.
Таблица 2. Экспериментальные прогибы центра тяжести панели
|
Параметр |
Ветровое давление, кПа |
|||||
|
Отрицательное w_p |
Положительное w+p |
|||||
|
- 0,69 |
- 0,91 |
- 1,26 |
- 1,67 |
0,74 |
0,97 |
|
|
Прогиб , мм |
-1,839 |
-2,457 |
-3,353 |
-4,366 |
2,130 |
2,559 |

Рис. 2. Экспериментальные исследования полномасштабноймодели стеновой панели.
В зависимости от геометрических и физических параметров стеновой панели были определены и введены в расчет прочности и жесткости коэффициенты податливости соединения каркаса и обшивки:kжк моменту инерции для расчёта прогиба и коэффициент kwк моменту сопротивления для расчета на прочность [1].
|
|
|
|
Где:
![]() момент инерции центрального I-образного сечения панели;
момент инерции центрального I-образного сечения панели; ![]() момент инерции отдельных слоев, равный сумме моментов инерции слоев обшивки и каркаса; S - статический момент одного листа обшивки;
момент инерции отдельных слоев, равный сумме моментов инерции слоев обшивки и каркаса; S - статический момент одного листа обшивки; ![]() число швов в составном элементе; E - модуль упругости при изгибе, принимаем с учетом длительной работы материалов;
число швов в составном элементе; E - модуль упругости при изгибе, принимаем с учетом длительной работы материалов; ![]() деформации соединений при полном их использовании (табл. 18, [3]); e - расстояние между нейтральными осями листов обшивки;
деформации соединений при полном их использовании (табл. 18, [3]); e - расстояние между нейтральными осями листов обшивки; ![]() - расчетный пролет панели;
- расчетный пролет панели; ![]() число связей в одном шве на весь пролет;
число связей в одном шве на весь пролет; ![]() расчетная несущая способность одной связи.
расчетная несущая способность одной связи.
Указанные коэффициенты в данном случае определены применительно только к расчету панели на воздействие горизонтальной (ветровой) нагрузки, т.к. при работе из плоскости панель обладает меньшей жесткостью. По расчетам получены следующие величины коэффициентов: kж=0,22 и kw=0,25. Расчетные напряжения и прогибы панелей с учетом податливости связей каркаса и обшивок приведены в табл. 3.
Таблица 3. Расчетные прогибы и напряжения в панели
|
Параметр |
Ветровое давление, кПа |
|||||
|
Отрицательное w_p |
Положительное w+p |
|||||
|
- 0,69 |
- 0,91 |
- 1,26 |
- 1,67 |
0,74 |
0,97 |
|
|
Напряжение |
0,124 |
0,160 |
0,218 |
0,286 |
0,134 |
0,170 |
|
Прогиб |
- 2,10 |
- 2,77 |
- 3,84 |
- 5,09 |
2,29 |
2,96 |
Оценка несущей способности панели по I группе предельных состояний производилась в результате анализа возникающих в ней напряжений. Для их определения в ПК SCAD была задана модель панели в конечных элементах (рис. 3), на которой была выполнена имитация ветровых воздействий, различных по знаку и величине (табл. 1).
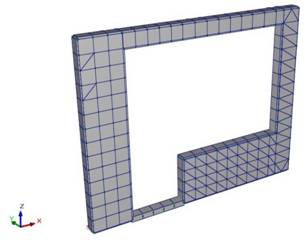
Рис. 3. Общий вид конечно-элементной модели стеновой панели
Деревянные элементы каркаса моделировались с помощью пластинчатых конечных элементов с ортотропными характеристиками жесткости [2]. Применение конечных элементов такого типа позволяет учесть анизотропию древесины. Коэффициенты Пуассона, модули упругости и модуль сдвига древесины задавались в соответствии с [4]. Листы обшивки панели из ЦСП моделировались с помощью пластинчатых конечных элементов с изотропными характеристиками жесткости (коэффициент Пуассона - 0,2,модуль упругости - 3000 МПа). Скобы, скрепляющие листы обшивки и каркас, были выполнены в виде конечных элементов, моделирующих связи конечной жесткости, устанавливаемых между двумя узлами и обеспечивающих взаимную линейную или угловую податливость узлов [2]. При этом учитывалась податливость соединения скобами в соответствии с выведенными ранее ее показателями. Закрепление панели было условно принято как шарнирно-неподвижное в трех точках верхней и нижней частей конструкции.
К расчетной схеме были приложены: собственный вес элементов каркаса и обшивки, пиковая ветровая нагрузка, пульсационное ветровое нагружение. При выполнении расчета соблюдались требования и рекомендации [3] и [4]. Динамический расчет системы был выполнен с использованием разложения по формам собственных колебаний (не более 6, согласно [3] для пульсации ветрового потока). Давление ветра на стеновую панель рассматривалось как сумма статической и пульсационной составляющих ветровой нагрузки. Усилия в элементах системы и перемещения ее точек находились раздельно от статической составляющей ветровой нагрузки и от инерционных сил, соответствующих каждой форме собственных колебаний. При этом считалось, что колебания совершаются вокруг смещенного состояния равновесия, соответствующего статической (средней) компоненте нагружения.
Результаты конечно-элементного моделирования (табл. 4) показали, что напряжения в элементах каркаса не превышают допускаемых при наиболее невыгодном сочетании усилий. Деформации не превысили предельно допустимых значений [4]. Следовательно, прочность стеновой панели обеспечена при данном шаге расстановки скоб и воздействии данных нагрузок.
Таблица 4. Прогибы и напряжения в элементах панели, согласно КЭ-моделирования
|
Параметр |
Ветровое давление, кПа |
||||||
|
Отрицательно w_p |
Положительное w+p |
||||||
|
- 0,69 |
- 0,91 |
- 1,26 |
- 1,67 |
0,74 |
0,97 |
||
|
Напряжение, МПа |
Обшивка |
0,11 |
0,15 |
0,16 |
0,27 |
0,12 |
0,15 |
|
Каркас |
1,47 |
1,95 |
2,71 |
3,6 |
1,58 |
2,08 |
|
|
Прогиб , мм |
-1,883 |
-2,483 |
-3,438 |
-4,557 |
2,188 |
2,647 |
|
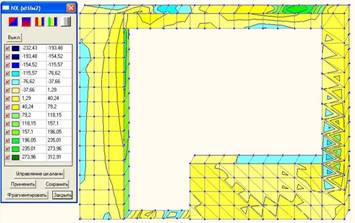
Рис. 4. Результаты КЭ-моделирования: нормальные напряжения Nx, кН/м2
Выводы:
- определён рациональный шаг установки крепежных скоб, равный 0,2 м при воздействии ветровых давлений на высоте 28 и 75 м (II ветровой район, тип местности В), при котором обеспечиваются прочность и жесткость панели;
- для учета податливости соединения каркаса и листов ЦСП и повышения точности расчетов определены коэффициент к моменту инерции -kж=0,22 (коэффициент жесткости составного элемента на податливых соединениях) и коэффициент к моменту сопротивления -kw=0,25;
- компьютерное моделирование сопротивления конструкции воздействию ветровой нагрузки показало хорошую сходимость данных по прогибам с экспериментом - 2-4 % (табл. 2, 4), что позволяет рекомендовать использование при проектировании стеновых панелей на деревянном каркасе с обшивками из листов ЦСП метода конечных элементов для определения напряжений и деформаций в конструкции, а следовательно, ее прочности и жесткости.
Рецензенты:
Серов Е. Н., д.т.н., профессор кафедры конструкций из дерева и пластмасс ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург.
Лабудин Б. В., д.т.н., профессор кафедры инженерных конструкций и архитектуры ИСиА ФГАОУ ВПО «Северный (Арктический) федеральный университет имени М. В. Ломоносова», г. Архангельск.




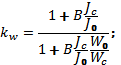 (2)
(2)