Одна из важнейших целей моделирования заключается в прогнозировании поведения исследуемого объекта. Прогнозирование финансовых временных рядов является одной из наиболее важных задач при построении инвестиционной стратегии инвестора - принятии решения о покупке (продаже) финансовых инструментов. В настоящее время для прогнозирования поведения финансовых инструментов все чаще используется фрактальный анализ.
1. Индекс фрактальности и построение инвестиционной стратегии на основе свойств временного ряда
Фрактал - это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба. Для эффективного рынка верно положение, которое Мандельброт называет «скейлинговым принципом изменения цен» [5]. Этот принцип означает, что на графиках цен выделяются области, называемые фракталами.
Индекс фрактальности находится как коэффициент наклона линии линейной регрессии y = ax + b, построенной по точкам с абсциссами и ординатами ln (δ), ln(V(δ)), где δ = 1,2,4,8,16,32 то есть [3]:
μ = - a (1)
где μ - индекс фрактальности,
δ - масштаб разбиения, содержащий Q = 25-m точек, соответствующих торговым дням, где ![]() , - амплитудная вариация финансового ряда, соответствующая масштабу разбиения δ, рассчитанная по формуле:
, - амплитудная вариация финансового ряда, соответствующая масштабу разбиения δ, рассчитанная по формуле:
![]() (2)
(2)
где Pimax и Pimin максимальная и минимальная цены финансового инструмента на i-том разбиении масштаба δ.
Индекс фрактальности отражает свойства временных рядов, связанные с поведением последующих значений временного ряда на основе поведения предыдущих. Эти свойства называют свойствами памяти временного ряда (табл.1).
Таблица 1
Свойства временных рядов на основе индекса фрактальности
|
μ = 0,5 |
0,5 < μ ≤ 1,0 |
0 < μ ≤ 0,5 |
|
Отсутствие памяти |
«Отрицательная» память |
Положительная память |
Исходная выборка дневных доходностей может быть разбита на три непересекающихся выборки, соответствующие различным состояниям исходного временного ряда с учетом количества дней с начала растущего тренда n1 или с учетом количества дней с начала падающего тренда - n2:
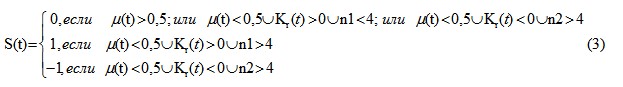 (3)
(3)
μ (t) - текущее значение индекса фрактальности, рассчитанное для ![]() интервалов, предшествующих n = 5 точкам;
интервалов, предшествующих n = 5 точкам;
Kr (t) - коэффициент наклона линии линейной регрессии, рассчитываемый по 16-ти предшествующим точкам [3, стр. 39].
Условия (4) показывают наличие или отсутствие устойчивого тренда и позволяют построить прогноз для состояния ряда.
Алгоритм построения прогноза на основе фрактальных свойств выглядит следующим образом:
1) Для каждого значения временного ряда, начиная с 33-го значения, рассчитывается индекс фрактальности μ (t) и коэффициент регрессии Kr (t).
2) Задаются счетчики длительности трендов n1, n2.
3) По значениям μ (t), Kr (t) и по длительности трендов n1, n2 делается вывод о состоянии ряда S(t) :
- если S(t)=0, то временной ряд находится в состоянии хаотического движения и прогнозное значение доходности будет равно значению доходности в предыдущей точке;
- если S(t)=±1, то прогнозное значение получим, используя регрессию по четырем предыдущим точкам.
Алгоритм построения прогноза на основе фрактальных свойств был применен для построения стратегии управления инвестиционным портфелем:
- покупки финансового инструмента следует совершать при устойчивом растущем тренде, т.е. S(t)=1;
- продажи следует осуществлять при смене состояния S(t)<>1.
Для исследования в качестве экспериментальных данных были взяты 10 финансовых инструментов, выбранных случайным образом из финансовых инструментов российского рынка. Для расчетов использовали доходности акций за период с 12 сентября 2007 г. по 14 сентября 2011 г. (всего 992 наблюдений).
2. Прогноз доходности на основе многофакторной регрессионной модели
В настоящее время для выявления закономерностей в отсутствии априорных знаний об их существовании, когда изучается взаимосвязь двух и более величин (переменных), успешно применяются регрессионные модели [1].
Для эффективного формирования портфеля вычисляют однодневные доходности.
Уравнение регрессии для каждого наблюдения ежедневной доходности запишется следующим образом:
![]() (4)
(4)
где xtp - значение независимой переменной xp в наблюдении t; n - количество наблюдений, p - количество независимых переменных.
В качестве зависимой переменной используется доходность финансового инструмента. В качестве независимых величин (переменных) выступают рыночные факторы. Рыночные факторы представляют собой макроэкономические показатели финансовой системы: индексы международных рынков ценных бумаг, мировые цены на энергоресурсы и полезные ископаемые, индексы государственных и корпоративных облигаций, процентные ставки на межбанковском рынке, курсы валют и др. Рыночные факторы можно подразделить на группы, в зависимости от природы индикатора: валютные, товарные, процентные и фондовые.
Для определения вида линейной многофакторной регрессии в модели использовалось 38 независимых переменных (k =38), представленных на временном интервале с 12 сентября 2007 г. по 14 сентября 2011 г. (всего 992 наблюдений) для всех, выбранных для исследования финансовых инструментов. Из них: 23 фондовых показателя, 1 валютный, 9 товарных, 5 процентных. Для расчета коэффициентов регрессионной модели был использован алгоритм пошагового включения. После применения процедуры пошагового включения переменных получили математические модели доходности финансовых инструментов, включающие следующие независимые переменные из исходных 38 переменных (таблица 1):
Результаты построения прогнозов доходности финансовых инструментов с использованием многофакторной регрессионной модели
Таблица 2
|
Параметры |
Валютные факторы |
Товарные факторы |
Фондовые факторы |
Процентные факторы |
Коэффициент детерминации R2 |
Прогноз доходности |
Прогноз Цены |
Реальная цена |
Отклонение от реального значения % |
|
«Газпром» |
0 |
4 |
17 |
1 |
68,0% |
0,01 |
167,539 |
166,0 |
0, 93% |
|
«Лукойл» |
1 |
5 |
19 |
2 |
70,0% |
-0,01763 |
1696,562 |
1733 |
2,10% |
|
«Ростелеком» |
1 |
5 |
18 |
3 |
71,0% |
0,011875 |
163,8124 |
164,96 |
0,70% |
|
«СНГ» |
1 |
5 |
15 |
2 |
67,5% |
0,032 |
24,45014 |
25,078 |
2,50% |
|
«Сбербанк» |
1 |
6 |
13 |
0 |
67,0% |
-0,032 |
77,47872 |
80,9 |
4,23% |
|
«Роснефть» |
1 |
3 |
16 |
2 |
68,5% |
0,02625 |
221,4648 |
217,28 |
1,93% |
|
«Новатек» |
0 |
5 |
13 |
0 |
69,5% |
-0,0205 |
377,0977 |
401 |
5,96% |
|
«Полюс» |
0 |
6 |
14 |
3 |
69,0% |
-0,02338 |
1806,854 |
1856,6 |
2,68% |
|
«СНГ» |
1 |
5 |
15 |
2 |
67,5% |
0,033 |
209,2238 |
205,66 |
1,73% |
|
«МТС» |
1 |
7 |
16 |
1 |
70,5% |
-0,0011 |
82,9087 |
84,32 |
1,67% |
|
«НЛМК» |
1 |
7 |
17 |
1 |
71,5% |
-0,01763 |
1696,562 |
1733 |
2,10% |
|
Среднее |
|
|
|
|
|
|
|
|
2,44% |
Для моделей из таб. 1 коэффициенты детерминации R2 принимают значения в диапазоне от 68 % до 71,5 %, что говорит о высоком качестве моделей.
Прогноз доходности финансовых инструментов на один шаг вперед определялся, как:
![]() (5)
(5)
где ![]() -
- ![]() матрица (вектор-столбец)
матрица (вектор-столбец) ![]() вектор независимых переменных относительных приращений рыночных факторов.
вектор независимых переменных относительных приращений рыночных факторов. ![]() вектор коэффициентов;
вектор коэффициентов; ![]() вектор ошибок.
вектор ошибок.
Рассчитанные предсказанные значения доходностей финансовых инструментов определяют цену. Предсказанные значения цены финансовых инструментов мало отличаются от реальных значений, отклонения колеблются в диапазоне 0,7 % до 5,96 %, среднее значение отклонения равно 2,44 %.
3. Прогноз доходности на основе нейросетевой модели
Применение модели нейронных сетей оправдывает себя при решении задач, в которых не представляется возможным учесть все реально имеющиеся условия, а можно лишь выделить приблизительный набор наиболее важных условий [2].
Для решения задачи прогнозирования необходимо найти такую нейронную сеть, которая бы наилучшим образом строила отображение F: X→Y, обобщающее сформированный на основе ценовой динамики набор примеров { xk , yk}. Воспользуемся факторами, полученными методом пошагового отбора для регрессионной модели. Для построения прогноза воспользуемся двухслойной сетью обратного распространения, которая может обучаться с помощью процедуры обратного распространения [4].
Результаты тестирования моделей нейронных сетей для 10 финансовых инструментов из таб. 1 представлены в Таблице 3.
Результаты построения прогнозов стоимости финансовых инструментов с использованием нейронной модели
Таблица 3
|
Параметры |
Шаг обучения |
Ошибка оценки |
Прогноз доходности |
Прогноз Цены |
Реальная цена |
Отклонение от реального значения, % |
|
«Газпром» |
4060 |
0,0036 |
0,0021 |
166,2283 |
166 |
0,14% |
|
«Лукойл» |
3940 |
0,0012 |
0,00375 |
1733,476 |
1733 |
0,03% |
|
«Ростелеком» |
530 |
0,003 |
0,016 |
164,4802 |
164,96 |
0,29% |
|
«СНГ» |
180 |
0,004 |
0,051 |
24,90029 |
25,078 |
0,71% |
|
«Сбербанк» |
219 |
0,0022 |
0,0048 |
80,42419 |
80,9 |
0,59% |
|
«Роснефть» |
1211 |
0,0039 |
-0,0045 |
214,8289 |
217,28 |
1,13% |
|
«Новатек» |
1342 |
0,0041 |
0,038 |
399,6196 |
401 |
0,34% |
|
«Полюс» |
1542 |
0,0019 |
0,00425 |
1857,963 |
1856,6 |
0,07% |
|
«МТС» |
1982 |
0,0026 |
0,0035 |
203,2489 |
205,66 |
1,17% |
|
«НЛМК» |
1642 |
0,0048 |
0,003 |
83,249 |
84,32 |
1,27% |
|
среднее |
|
0,0031 |
|
|
|
0,57% |
Предсказанные значения доходностей финансовых инструментов ![]() определяют соответствующие предсказанные цены. Предсказанные значения цены незначительно отличаются от реальных значений, разброс отклонений составляет диапазон от 0,03 % до 1,17 %, среднее значение отклонения равно 0,57 %. Сравнение средней точности прогнозов нейросетевой модели и линейной регрессионной модели (0,57% <2,44%) говорит о более высокой точности прогнозов на основе нейронной сети.
определяют соответствующие предсказанные цены. Предсказанные значения цены незначительно отличаются от реальных значений, разброс отклонений составляет диапазон от 0,03 % до 1,17 %, среднее значение отклонения равно 0,57 %. Сравнение средней точности прогнозов нейросетевой модели и линейной регрессионной модели (0,57% <2,44%) говорит о более высокой точности прогнозов на основе нейронной сети.
4.1. Построение инвестиционной стратегии на основе математических моделей: многофакторной регрессионной модели и нейронной сети
Воспользуемся полученными результатами для построения стратегии инвестора при формировании портфеля финансовых инструментов. Пусть инвестор принимает решение о покупке и продаже бумаг ежедневно, основываясь на прогнозе ![]() ,
, ![]() где
где ![]() - прогноз нейронной сети,
- прогноз нейронной сети, ![]() - прогноз многофакторной регрессионной модели, и знаний статистического анализа о средней дневной доходности финансового инструмента. Индикаторами покупки будут выступать следующие показатели, представленные в таблице 4.
- прогноз многофакторной регрессионной модели, и знаний статистического анализа о средней дневной доходности финансового инструмента. Индикаторами покупки будут выступать следующие показатели, представленные в таблице 4.
Индикаторы принятия решения о покупке инвестором
Таблица 4
|
Индикатор |
условие |
|
Значение прогноза доходности нейронной сети на след. день, |
yt > β |
|
Цена открытия больше цены закрытия предыдущего дня
|
|
|
Прогноз доходности по регрессии, построенной по четырем предыдущим точкам |
|
Параметр β отражает склонность инвестора к риску. Коэффициент β использовался для оценки нижней границы прогнозируемой доходности, устанавливаемой инвестором. Будем рассматривать значения β в диапазоне от 0,015; 0,045 (уровень дневной доходности операций находится в диапазоне от 1,5 % до 4,5 %), т. е. умеренной склонности к риску, с шагом 0,001.
Параметр ![]() отражает точность построенного прогноза и характеризует отношение прогнозного значения по отношению к реальному значению. Будем рассматривать значения
отражает точность построенного прогноза и характеризует отношение прогнозного значения по отношению к реальному значению. Будем рассматривать значения ![]() в диапазоне от 1 до 2,2, что соответствует разбросу дневной доходности операций в диапазоне от 1,5 % до 9,9 % и соответствует хорошей точности прогнозов.
в диапазоне от 1 до 2,2, что соответствует разбросу дневной доходности операций в диапазоне от 1,5 % до 9,9 % и соответствует хорошей точности прогнозов.
При тестирования параметров использовался показатель ![]() - «чувствительность», отражающий качество прогноза, а именно относительное число случаев, когда реальное значение доходности охватывалось интервальным прогнозом с вероятностью 99 %:
- «чувствительность», отражающий качество прогноза, а именно относительное число случаев, когда реальное значение доходности охватывалось интервальным прогнозом с вероятностью 99 %:
![]() , (6)
, (6)
где p - число прогнозов, подтвержденных фактическими данными, q - число прогнозов, не подтвержденных фактическими данными.
При выполнении условий принятия решений инвестором о покупке из таблицы 4 возможно инвестор принимает решение на основе алгоритма 1.
Алгоритм 1 принятия решения инвестором
1) Покупки совершаются при выполнении индикаторов принятия решения (таб. 4) по цене ![]() , количество бумаг:
, количество бумаг: ![]() ; заявка на продажу выставляется по цене
; заявка на продажу выставляется по цене 
2) В случае выполнения прогноза по финансовому инструменту в текущий день инвестор получает доход: ![]()
3) В случае невыполнения прогноза по финансовому инструменту в текущий день, т.е. если 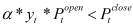 или
или 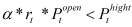 , инвестор принимает решение оставить бумагу до следующего дня.
, инвестор принимает решение оставить бумагу до следующего дня.
Через день выполняются шаги алгоритма 1-3 для t=t+1, только в п.3 инвестор фиксирует убыток: 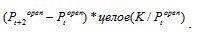 .
.
Тестирование инвестиционной стратегии по алгоритму 1 проводилось для 10 финансовых инструментов. Таблицы 5 и 6 демонстрируют результаты тестирования стратегии для финансовых инструментов за период с 12 сентября 2007 г. по 14 сентября 2011 г. (всего 992 наблюдений).
Тестирование стратегии для многофакторной регрессионной модели различных финансовых инструментов с целью нахождения параметров α и β
Таблица 5
|
|
«Газпром» |
«Лукойл» |
«Ростелеком» |
«СНГ» |
«Сбербанк» |
«Роснефть» |
«Новатек» |
«Полюс» |
«МТС» |
«НЛМК» |
|
β |
0,015 |
0,017 |
0,015 |
0,02 |
0,015 |
0,016 |
0,016 |
0,016 |
0,015 |
0,015 |
|
α |
1,1 |
1,1 |
1,9 |
2,2 |
1,8 |
1,7 |
1,7 |
2,2 |
2,2 |
2,2 |
|
Общее количество покупок, p+q |
86 |
71 |
63 |
87 |
85 |
82 |
99 |
106 |
82 |
105 |
|
Количество удачных покупок p |
70 |
62 |
41 |
74 |
73 |
69 |
81 |
88 |
66 |
78 |
|
Чувствительность, ν % |
0,8139 |
0,8473 |
0,7669 |
0,8505 |
0,8588 |
0,84146 |
0,81818 |
0,8302 |
0,8048 |
0,7429 |
|
Размер убытка, руб |
52260 |
17818,6 |
91378,9 |
30698 |
56220,3 |
29077,9 |
42421,0 |
58432,5 |
46404 |
107230 |
|
Доходность с учетом убытка, % |
32,98% |
82,08% |
49,55% |
80,69% |
119,07% |
74,14% |
86,87% |
79,53% |
35,36% |
90,42% |
Тестирование стратегии для нейронной модели различных финансовых инструментов с целью нахождения параметров α и β
Таблица 6
|
|
«Газпром» |
«Лукойл» |
«Ростелеком» |
«СНГ» |
«Сбербанк» |
«Роснефть» |
«Новатек» |
«полюс» |
«МТС» |
«НЛМК» |
|
β |
0,015 |
0,016 |
0,015 |
0,015 |
0,015 |
0,018 |
0,017 |
0,015 |
0,015 |
0,015 |
|
α |
1,9 |
1,9 |
2,1 |
2,2 |
2,2 |
2,2 |
2,2 |
2,1 |
2,2 |
2,2 |
|
Общее количество покупок, p+q |
62 |
62 |
79 |
96 |
71 |
53 |
86 |
53 |
43 |
88 |
|
Количество удачных покупок p |
54 |
46 |
67 |
78 |
65 |
46 |
74 |
43 |
39 |
62 |
|
Чувствительность, ν % |
0,870968 |
0,7419 |
0,8481 |
0,8125 |
0,8732 |
0,8679 |
0,8604 |
0,8113 |
0,9069 |
0,7045 |
|
Размер убытка, руб |
17673,3 |
2860 |
40381,6 |
49515,2 |
25043,7 |
7395,5 |
28072,4 |
0 |
19521,8 |
29642,0 |
|
Доходность с учетом убытка, % |
70,67% |
107,% |
44,4% |
81,41% |
116,3% |
102,9% |
104,9% |
154,26% |
41,93% |
187,87% |
В таблицах 5 и 6 представлены следующие поля:
общее количество покупок p+q; количество удачных покупок - число сделок p, когда прогноз выполнился; чувствительность прогноза ν; количество убытков - это количество случаев, когда прогнозное значение доходности было меньше реальной текущей доходности и ситуация на рынке через один день не позволила продать акцию без убытков, продажа осуществлялась по цене открытия через один день.
Для многофакторной регрессионной модели наибольшая доходность составила 119,07 % для акций ОАО «Сбербанк» за период с 12 сентября 2007 г. по 14 сентября 2011 г. (всего 992 наблюдений) при тестировании инвестиционной стратегии при параметрах ![]() и
и ![]() .
.
Для нейронной модели наибольшая доходность составила 187,87 % для акций ОАО «НЛМК» за период с 12 сентября 2007 г. по 14 сентября 2011 г. (всего 992 наблюдений) при тестировании инвестиционной стратегии при параметрах ![]() и
и ![]() .
.
Тестирование инвестиционной стратегии по алгоритму 1 для финансовых инструментов показало доходность в диапазоне от 32,98 % до 187,87 %. Наблюдается тенденция роста доходности с уменьшением показателя β и с ростом показателя α.
4. 2. Построение интегрированной инвестиционной стратегии с учетом фрактальных свойств
Для построения стратегии на основе синтеза прогнозов нейронной сети и регрессионной модели, а также с учетом фрактальных свойств воспользуемся определением состояния ряда (3) и результатами таблиц 5 и 6 согласно Алгоритму 2.
По Алгоритму 2 - принятия решения инвестором с учетом состояния ряда и прогнозов нейронной и регрессионной моделей - выполняются следующие шаги:
1) покупки совершаются при устойчивом растущем тренде, т.е. S(t)=1, а продажи осуществляется при смене состояния S(t);
2) в случае если S(t)<>1, то инвестор проверяет на применимость прогноза нейронной сети путем проверки индикаторов принятия решения (таб. 4) при ![]() ;
;
3) при выполнении индикаторов принятия решения (таб. 3) при ![]() инвестор использует алгоритм 1 с параметрами
инвестор использует алгоритм 1 с параметрами ![]() ;
;
4) при невыполнении индикаторов принятия решения (таб. 4) при ![]() инвестор проверяет на применимость прогноза регрессионной модели путем проверки индикаторов принятия решения (таб. 3) при
инвестор проверяет на применимость прогноза регрессионной модели путем проверки индикаторов принятия решения (таб. 3) при ![]() ;
;
5) при выполнении индикаторов принятия решения (таб. 4) при ![]() инвестор использует Алгоритм 1 с параметрами
инвестор использует Алгоритм 1 с параметрами ![]() ;
;
6) при невыполнении индикаторов принятия решения (таб. 4) при ![]() инвестор принимает решение не покупать акции и ждет завершение текущего торгового дня для построения прогноза на следующий день.
инвестор принимает решение не покупать акции и ждет завершение текущего торгового дня для построения прогноза на следующий день.
В результате тестирования улучшенной стратегии для акций за период с 12 сентября 2007 г. по 14 сентября 2011 г. (всего 992 наблюдений) получили следующие доходности:
Сравнение доходностей на основе различных стратегий
Таблица 7
|
Название стратегии/Бумага |
Стратегия на основе фрактальных свойств |
Стратегия на основе регрессионной модели |
Стратегия на основе нейронной сети |
Интегрированная стратегия |
Рейтинг |
|
«Газпром» |
19,8 % |
32,98% |
70,67% |
83,01% |
9 |
|
«Лукойл» |
17,9 % |
82,08% |
107,62% |
136,7% |
5 |
|
«Ростелеком» |
14,98% |
49,55% |
44,36% |
102,77% |
8 |
|
«СНГ» |
13,8% |
80,69% |
81,41% |
112,23% |
7 |
|
«Сбербанк» |
-0,02% |
119,07% |
116,31% |
150,7% |
3 |
|
«Роснефть» |
21,04% |
102,95% |
74,14% |
142,7% |
4 |
|
«Новатек» |
14,87% |
86,87% |
104,96% |
125,41% |
6 |
|
«Полюс» |
14,4% |
79,53% |
154,26% |
160,00% |
2 |
|
«МТС» |
11,7% |
35,36% |
41,93% |
71,28% |
10 |
|
«НЛМК» |
17,6% |
90,42% |
187,87% |
185,63% |
1 |
Сравнение доходностей стратегий (таб. 7) говорит о высоком уровне доходности интегрированной стратегии с учетом состояния ряда и прогнозов нейронной и регрессионной моделей. Определение состояний временного ряда на основе фрактальных характеристик позволило значительно улучшить качество прогноза и соответственно построить инвестиционную стратегию с большей доходностью.
ВЫВОДЫ
Рассмотрена задача построения и тестирования интегрированной инвестиционной стратегии формирования портфеля финансовых инструментов с использованием математических моделей и фрактальных свойств. В ходе тестирования полученной стратегии для 10 финансовых инструментов за период с 12 сентября 2007 г. по 14 сентября 2011 г. (всего 992 наблюдений) были получены следующие результаты: максимальная доходность в размере 185,63 % для акции ОАО «НЛМК», минимальная доходность в размере 71,28 % для акции ОАО «МТС». Определение состояний временного ряда на основе фрактальных характеристик позволило значительно улучшить качество прогноза и соответственно построить инвестиционную стратегию с большей доходностью.
Бахарев М. С., д.т.н., профессор, директор Сургутского Института нефти и газа ФГБОУ ВПО «ТюмГНГУ», г. Сургут.
Антонов А.В., д.т.н., профессор, ИАТЭ НИЯУ МИФИ, Калужская область, г. Обнинск.
Савин К. Н., д.э.н., профессор кафедры «Экономический анализ и качество», ФГБОУ ВПО «Тамбовский государственный технический университет», г. Тамбов.



