Для современной техники характерна тенденция по резкому повышению теплонапряженности элементов конструкций. В этих условиях вопросы контактного теплообмена приобретают существенное значение. Об этом свидетельствуют многочисленные отечественные и зарубежные исследования последних десятилетий [2, 3, 6, 9]. Как экспериментальные, так и теоретические исследования показали, что вследствие большого числа факторов, оказывающих влияние на теплообмен в зоне контакта твердых тел, решение этой проблемы далеко от завершения. Остается без ответа целый ряд вопросов по формированию контактного термосопротивления (КТС) для условий, близких к реальным. В частности, к разряду малоизученных следует отнести вопросы направленного терморегулирования в составных теплонапряженных системах путем введения в зону контакта различных заполнителей [7, 8]. Во-первых, проведенные экспериментальные исследования ограничены малым набором заполнителей, вводимых в контактную зону, и, во-вторых, практически отсутствует теоретическая проработка возможности применения заполнителей для конкретных условий функционирования теплового контакта. По сути дела эта проблема решалась по мере возникновения необходимости повышать или снижать тепловую проводимость через зону контакта составных деталей и узлов.
Цель исследования. Результаты исследования
В данном сообщении ставится задача на основе обширного экспериментального материала для заполнителей различной природы, при разных условиях контакта сделать обобщающие выводы и рекомендации для проведения операций по терморегулированию технических систем с контактными переходами. Экспериментальная программа исследований реализовывалась на специальной установке для изучения контактного теплообмена. Основу установки составляет рабочая ячейка из двух тепломеров в виде контактирующих торцами вертикально расположенных латунных стержней длиной 100 мм и диаметром 30 мм каждый. Верхний стержень выполняет функции электронагревателя, нижний - водяного холодильника. Каждый стержень имеет по пять радиальных сверлений диаметром 1,5 мм на расстоянии 10 мм друг от друга на глубину 15 мм, в которые монтируются хромель-копелевые термопары. Электродвижущая сила, развиваемая термопарами, измеряется компенсационным методом при помощи потенциометра. Боковые поверхности стержней теплоизолированы. Осевое нагружение в зоне контакта осуществляется путем установки набора грузов. Для определения термосопротивления в зоне контакта металлических поверхностей Rk применяется метод, в основу которого положен закон Фурье и дифференциальное уравнение теплопроводности для неограниченной пластины с изотермическими поверхностями при стационарных условиях теплового режима. КТС рассчитывалось по формуле
![]() , (1)
, (1)
где температурный перепад в зоне контакта ![]() определялся из графика изменения температуры по длине стержней;
определялся из графика изменения температуры по длине стержней; ![]() - средняя величина теплового потока, которая находилась по градиентам температур в верхнем и нижнем стержнях по формулам:
- средняя величина теплового потока, которая находилась по градиентам температур в верхнем и нижнем стержнях по формулам:
для верхнего стержня ![]() ; для нижнего стержня
; для нижнего стержня ![]() (2)
(2)
Здесь ![]() - соответственно коэффициенты теплопроводности материалов верхнего и нижнего стержней;
- соответственно коэффициенты теплопроводности материалов верхнего и нижнего стержней; ![]() - температурные перепады между смежными точками, где установлены термопары;
- температурные перепады между смежными точками, где установлены термопары; ![]() - расстояние между смежными точками.
- расстояние между смежными точками.
При известных ![]() и
и ![]() находился средний тепловой поток через зону контакта
находился средний тепловой поток через зону контакта
![]() (3)
(3)
В качестве заполнителей межконтактного пространства использовались асбестовый лист, железная сетка с оксидной пленкой и обработанная растворителем, сетки из нержавеющей стали из различной по толщине проволоки и разного размера ячеек.
Для исследуемых заполнителей проведены две серии опытов при средних значениях температуры в зоне контакта tk = 65 ºС и tk = 130 ºС. Изменялось усилие прижима Р от 0,2 до 0,85 МПа. Применяемое усилие прижима в зоне контакта относится к категории малых нагрузок [7]. Полученные в процессе проведенных исследований зависимости ![]() представлены на рис. 2 и 3.
представлены на рис. 2 и 3.
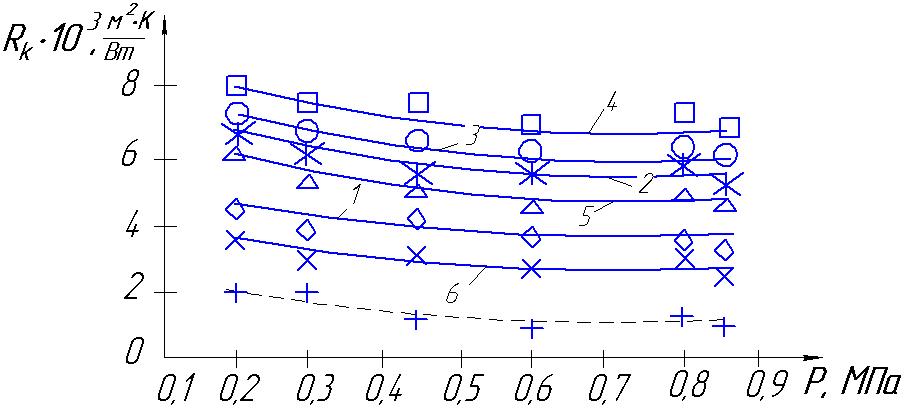
Рисунок 1. Зависимость термосопротивления от нагрузки при tк =65ºС для заполнителей в зоне контакта: 1 - асбест ( ![]() = 0,43 мм); 2 - железная сетка, обработанная растворителем (
= 0,43 мм); 2 - железная сетка, обработанная растворителем (![]() = 0,75 мм, размер ячейки 1 мм × 1 мм); 3 - та же железная сетка с оксидной пленкой; 4 - сетка из нержавеющей стали (
= 0,75 мм, размер ячейки 1 мм × 1 мм); 3 - та же железная сетка с оксидной пленкой; 4 - сетка из нержавеющей стали ( ![]() = 0,88 мм, 1 мм × 1 мм); 5 - сетка из нержавеющей стали (
= 0,88 мм, 1 мм × 1 мм); 5 - сетка из нержавеющей стали ( ![]() = 0,39 мм, 0,5 мм × 0,5 мм); 6 - сетка из нержавеющей стали (
= 0,39 мм, 0,5 мм × 0,5 мм); 6 - сетка из нержавеющей стали ( ![]() = 0,13 мм, 0,05 мм × 0,05 мм); штриховая линия - непосредственный контакт без прослойки.
= 0,13 мм, 0,05 мм × 0,05 мм); штриховая линия - непосредственный контакт без прослойки.

Рисунок 2. Зависимость термосопротивления от нагрузки при tк =130 ºС для заполнителей в зоне контакта: аналогично данным рис. 2.
Из анализа приведенных на рис. 1 и 2 опытных данных можно сделать следующие выводы. Наиболее высокие КТС создают соединения с заполнителями в виде сетки из нержавеющей стали с проволокой большей толщины (кривая 4). Для сетки из проволоки меньшей толщины и меньшего размера ячеек термосопротивление в зоне контакта значительно меньше (кривые 5 и 6). Подобный характер формирования КТС можно объяснить уменьшением толщины воздушной прослойки и ростом непосредственного контакта сетки с поверхностями нагревателя и холодильника. Сетка из железа (кривая 2) снижает термическое сопротивление по сравнению с сеткой из малотеплопроводной нержавеющей стали. Сетка из железной проволоки, покрытой оксидной пленкой, как и следовало ожидать, снижает тепловую проводимость контакта (кривая 3 по сравнению с кривой 2). Использование металлических сеток, особенно из нержавеющей стали, дает возможность создавать достаточно эффективную теплоизоляцию по сравнению, например, с листовым асбестом (кривая 1). При этом следует учитывать, что металлические соединения с заполнителями из сеток могут функционировать в режиме значительных механических нагрузок.
На величину КТС оказывает влияние температура в зоне контакта. Как видно из данных рис. 1 и 2, повышение температуры в зоне контакта заметно снижает КТС, что можно объяснить, в первую очередь, повышением коэффициента теплопроводности воздуха в зоне перехода с увеличением температуры. Для оценки различных сочетаний основного металла контактирующих поверхностей и материала вводимого в зону контакта заполнителя вводится безразмерный комплекс в виде отношения термосопротивления контактной зоны ![]() с несжатой прослойкой из материала заполнителя толщиной к термосопротивлению при непосредственном контакте Rk и эквивалентной толщины зазора Δ, т.е.
с несжатой прослойкой из материала заполнителя толщиной к термосопротивлению при непосредственном контакте Rk и эквивалентной толщины зазора Δ, т.е.
![]() (4)
(4)
По данным рис. 2 с помощью формулы (4) построены кривые зависимости ![]() на рис. 3.
на рис. 3.
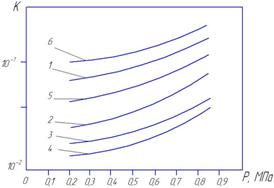
Рисунок 3. Зависимость безразмерного термосопротивления от нагрузки для различных заполнителей при tк =130ºС: аналогично данным рис. 2
Безразмерное термосопротивление имитирует контактное соединение с заполнителем, обладающим в последнем варианте бесконечным термосопротивлением на пути теплового потока. В реальных условиях высокие значения К характерны для заполнителей из хороших теплоизоляционных материалов. Если же безразмерное термосопротивление стремится к нулю, то система имеет контактное соединение с заполнителями из высокотеплопроводных материалов.
Как видно из графиков рис. 3, повышение давления в зоне контакта нивелирует различия в безразмерном термосопротивлении для различных заполнителей контактной зоны. Таким образом, при достаточно высоком значении давления можно считать, что различия в эффективности различных заполнителей станут незначительными.
Практическое использование выражения (4) для конкретных контактных соединений сопряжено с определенными трудностями. Термосопротивление прослойки из материала заполнителя Rпр в первом приближении может быть рассчитано при известной теплопроводности материала ![]() и замеренной толщины прослойки δ или найдено экспериментальным путем. Сложнее решается задача нахождения значения КТС при непосредственном касании поверхностей Rk. Здесь также возможны два варианта решения вопроса, т.е. можно найти Rk экспериментальным путем или использовать ранее полученные расчетные формулы. Для контактных соединений, работающих в режиме средних и высоких механических нагрузок (Р ≥ 10 МПа) [3], получены расчетные формулы, позволяющие находить Rk для конкретной контактной пары [2, 6, 9]. В то же время в практике наиболее часто встречаются теплонапряженные соединения, функционирующие в режиме малых механических нагрузок. Получение расчетных зависимостей для определения КТС в этом случае усложняется неопределенностью распределения фактических площадок контакта по номинальной поверхности соприкосновения поверхностей. Более корректными представляются формулы, полученные ранее [4] для контактных пар с плоскошероховатыми металлическими поверхностями.
и замеренной толщины прослойки δ или найдено экспериментальным путем. Сложнее решается задача нахождения значения КТС при непосредственном касании поверхностей Rk. Здесь также возможны два варианта решения вопроса, т.е. можно найти Rk экспериментальным путем или использовать ранее полученные расчетные формулы. Для контактных соединений, работающих в режиме средних и высоких механических нагрузок (Р ≥ 10 МПа) [3], получены расчетные формулы, позволяющие находить Rk для конкретной контактной пары [2, 6, 9]. В то же время в практике наиболее часто встречаются теплонапряженные соединения, функционирующие в режиме малых механических нагрузок. Получение расчетных зависимостей для определения КТС в этом случае усложняется неопределенностью распределения фактических площадок контакта по номинальной поверхности соприкосновения поверхностей. Более корректными представляются формулы, полученные ранее [4] для контактных пар с плоскошероховатыми металлическими поверхностями.
Для контактов плоскошероховатых поверхностей из высокопластичных металлов термосопротивление при наличии воздушной прослойки рассчитывается по формуле
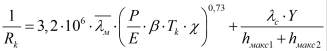 (5)
(5)
и для контактов из высокоупругих металлов
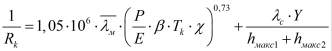 (6)
(6)
Здесь ![]() - соответственно коэффициенты теплопроводности металлов и межконтакной газовой среды; Е - модуль упругости метала контактной пары;
- соответственно коэффициенты теплопроводности металлов и межконтакной газовой среды; Е - модуль упругости метала контактной пары; ![]() - средняя температура в зоне контакта;
- средняя температура в зоне контакта; ![]() - максимальная высота микронеровностей поверхности контакта; β - коэффициент объемного расширения;
- максимальная высота микронеровностей поверхности контакта; β - коэффициент объемного расширения; ![]() - коэффициент, зависящий от суммы
- коэффициент, зависящий от суммы ![]() , который аналитически может быть интерпретирован в форме
, который аналитически может быть интерпретирован в форме
![]() при 5 ≥
при 5 ≥ ![]() ≥ 1 мкм;
≥ 1 мкм;
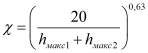 при 10 ≥
при 10 ≥ ![]() ≥ 5 мкм;
≥ 5 мкм;
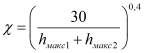 при 30 ≥
при 30 ≥ ![]() ≥ 10 мкм.
≥ 10 мкм.
Относительную величину зазора Y можно найти, используя кривые опорных поверхностей по снятым с поверхностей контакта профилограммам [1]. Таким же способом находится эквивалентная толщина межконтактной среды Δ.
Во многих случаях контакные поверхности имеют волнистость, которая оказывает существенное влияние на величину контактного сопротивления. Для расчета Rk можно использовать ранее полученные расчетные зависимости [5].
При контакте двух волнистых поверхностей
 (7)
(7)
и при контакте волнистой и плоскошероховатой поверхностей
 , (8)
, (8)
где ![]() - высота волны; L - шаг волны.
- высота волны; L - шаг волны.
В заключение следует отметить, что приведенные выше результаты исследований позволяют прогнозировать и направленно регулировать процесс теплообмена в теплонапряженных технических системах с контактными соединениями.
Рецензенты:
Бараков А.В., д.т.н., профессор, профессор кафедры теоретической и промышленной теплоэнергетики ФГБОУ ВПО «Воронежский государственный технический университет», г. Воронеж.
Мозговой Н.В., д.т.н., профессор, профессор кафедры промышленной экологии и безопасности жизнедеятельности ФГБОУ ВПО «Воронежский государственный технический университет», г. Воронеж.



