Полые объемные изделия, широко применяемые для вибро- и звукоизоляции полов и сидений в салонах легковых автомобилей, имеют сложную структуру и состоят из слоев газосодержащих полимерных материалов (например, пенополиэтилена, пенополиуретана), нетканых текстильных материалов (например, войлока) и (или) термопластов (например, полипропилена, акрилобутадиенстирола). Использование в качестве несущего слоя пористых материалов обусловлено тем, что они имеют высокие механические свойства, малую теплопроводность, хорошо изолируют звук и вибрации, так как эластичные перегородки ячеек являются плохими проводниками механических колебаний. В промышленности для изготовления таких изделий, отличающихся сложной конфигурацией, используется метод механического термоформования сопряженными матрицей и пуансоном, заключающийся в нагреве слоистого материала до температуры размягчения, его деформации при опускании пуансона и оформлении изделия, обе поверхности которого соответствуют размерам матрицы и пуансона.
Нагрев материала является ключевой стадией процесса, и нарушения его режима, связанные с неправильным выбором температуры и времени работы нагревателей или колебаниями температуры вследствие колебания напряжения в сети, сквозняка в цехе, приводят к возникновению различных дефектов формованных изделий, вызывающих снижение их физико-механических характеристик. Например, неравномерный нагрев или перегрев материала приводят к существенной разнотолщинности, образованию морщин и складок, пузырей, изменению цвета или разрыву изделия. Вытяжка недостаточно нагретого материала является причиной появления белого оттенка в сечении изделия [3]. Кроме того, различная усадка слоев материала, имеющих отличные друг от друга диапазоны температур формования, приводит к дополнительному короблению изделия. Поэтому необходимо вести разогрев материала так, чтобы распределение температуры по площади листа и по толщине его слоев было однородным в любой момент времени. На производстве автоматический контроль температуры материала не осуществляется, и формовщики подбирают температуру и время обогрева по результатам субъективной визуальной оценки степени готовности материала к вытяжке в высокоэластическом состоянии и на основе собственного опыта. Это может вести к браку в изделиях или к невозможности их формования вследствие быстрой гравитационной вытяжки материала, нагретого существенно выше температуры текучести. Таким образом, актуальной научной проблемой является разработка физически обоснованной математической модели нагрева, позволяющей повысить информационную мощность объекта (путем расчета переменного во времени температурного профиля по толщине материала) и определить управляющие воздействия, обеспечивающие снижение неоднородности температурного профиля до допустимых значений.
Основными методами нагрева слоистых полимерных и полимерно-текстильных материалов толщиной до 0,010-0,015 м являются радиационный (с использованием открытых нагревателей инфракрасного излучения) и контактный (путем прижатия листа к нагретой ТЭНами металлической плите), так как они обеспечивают меньшую продолжительность нагрева по сравнению с конвективным методом. Принудительный обдув материала горячим воздухом применяется в основном для полимеров, температура размягчения которых близка к температуре деструкции (например, полиметилметакрилат). От обогреваемой поверхности в массу материала тепло распространяется путем теплопроводности. Характеристика процесса нагрева материала представлена на рис. 1.
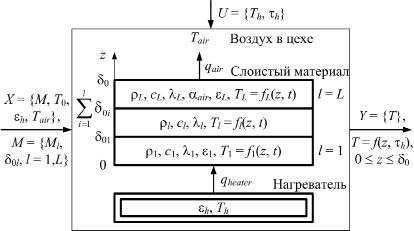
Рис.1. Характеристика процесса нагрева слоистого материала
На рис. 1 использованы следующие обозначения: X, U, Y - векторы входных параметров, управляющих воздействий и выходных параметров; M - тип материала; T0 - начальная температура материала, °С; εh - степень черноты радиационного нагревателя; Tair - температура воздуха в цехе, °С; Ml, δ0l - тип и толщина (м) материала l-го слоя; L - число слоев; Th - температура излучающей поверхности нагревателя (при радиационном нагреве) или греющей плиты (при контактном нагреве), °С; τh - время нагрева, с; z - координата по толщине материала, м; ρl, cl, λl - плотность (кг/м3), средняя удельная теплоемкость (Дж/(кг⋅°С)) и теплопроводность (Вт/ (м⋅°С)) материала слоя; ε1, εL - степени черноты наружных слоев материала; αair - коэффициент теплоотдачи к воздуху, Вт/(м2⋅°С); Tl - температура слоя, °С; t - время, с; qair - удельный конвективный тепловой поток от материала к воздуху, Вт/м2; qheater - удельный лучистый тепловой поток от нагревателя к материалу, Вт/м2; T - температура материала в конце нагрева, °С.
Теплообмен нейтральной поверхности материала с воздухом происходит при одностороннем радиационном и контактном нагреве. Толстые листовые материалы нагревают, как правило, при двухстороннем расположении радиационных нагревателей, чтобы избежать большого температурного градиента по толщине и возможной термической деструкции материала на обогреваемой поверхности. В этом случае в предложенное формализованное описание (в вектор U) добавляется температура верхнего нагревателя.
Задача управления стадией нагрева процесса термоформования, решаемая по модели, заключается в следующем. Для заданного типа M слоистого материала, имеющего начальную температуру T0 и нагреваемого заданным способом (радиационным или контактным) определить такие значения управляющих воздействий U, при которых выполняется требование к неоднородности температуры по толщине листа ∆T в конце стадии нагрева
![]() ,
,
где Tmax - максимально допустимая температура формования материала слоя, обращенного к нагревателю, °С; Tmin - минимальная температура формования материала нейтрального слоя при одностороннем или среднего слоя при двухстороннем нагреве, °С.
Анализ литературных источников и результатов экспериментальных исследований позволил сформировать следующие допущения, учитывающие характеристики материалов и процесса:
1) нагреваемый материал представляет собой одномерную слоистую систему с поперечным направлением тепловых потоков, характеризующуюся идеальным контактом слоев между собой;
2) нагрев осуществляется за счет теплопередачи от нагревателей путем лучеиспускания (при радиационном нагреве) и теплопроводности (при контактном нагреве) и вследствие теплопроводности внутри материала; при одностороннем радиационном и контактном нагреве охлаждение происходит в результате теплоотдачи окружающему воздуху путем конвекции и лучеиспускания;
3) теплофизические характеристики материалов слоев не изменяются при нагреве [4]; плотность ρ, теплоемкость c и теплопроводность λ пеноматериалов рассчитываются по формулам:
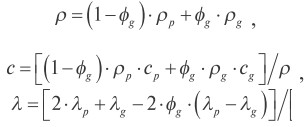 , (1)
, (1)
где φg - объемная доля газовой фазы (воздуха) в пеноматериале; индекс «p» относится к полимерной матрице, индекс «g» - к газу;
1) тепловой поток, направленный от радиационного нагревателя к единице поверхности материала, рассчитывается в соответствии с законом Стефана-Больцмана при условии, что излучающие тепло поверхности нагревателя и материала равны и параллельны:
![]() , (2)
, (2)
где Ch-m - коэффициент взаимного теплового излучения, равный
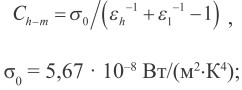 (3)
(3)
2) при контактном нагреве прижатие материала к греющей плите является идеальным, микрозазоры отсутствуют, поэтому локальное тепловое сопротивление в месте контакта пренебрежимо мало;
3) при одностороннем радиационном нагреве тепловой поток от единицы поверхности материала к воздуху с учетом того, что площадь поверхности излучения материала значительно меньше площади формовочного цеха, вычисляется по формуле:
![]() (4)
(4)
При контактном нагреве в формулу (4) подставляется температура нижней поверхности T1(0, t). При двухстороннем радиационном нагреве тепловые потоки qheater(i), i = 1, 2 определяются по формулам (2), (3) с учетом характеристик нагревателей (Th(i) , εh).
Модель нагрева, построенная путем применения закона сохранения энергии к неподвижной многослойной среде, имеет вид:
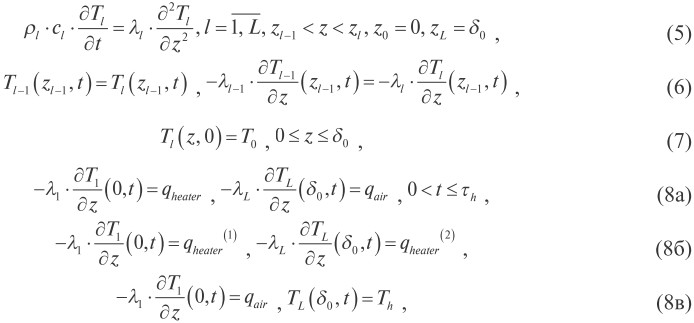
где z l-1 - координата границы контакта (l-1)-го и l-го слоев, м.
Равенства (6) выражают условия идеального теплового контакта слоев. Граничные условия (8а), (8б) и (8в) относятся к одностороннему, двухстороннему лучистому и контактному обогреву.
Переменная размерность системы уравнений теплового баланса, зависящая от числа слоев в материале, и нелинейность граничных условий предопределяют использование для расчета поля температуры численных методов. Одним из наиболее распространенных среди этих методов благодаря своей универсальности, наглядности физической интерпретации и простоте программной реализации является метод сеток. Разностная аппроксимация уравнений (5) выполнена по методу Лаасонена (двухслойная чисто неявная схема), обеспечивающему первый порядок точности по времени и второй порядок точности по пространственной координате [2]. Уравнения теплопроводности (5) являются параболическими, поэтому использование аппроксимаций первого порядка точности (двухточечных разностей) для производных в граничных условиях приводит к повышению погрешности численного решения. В связи с этим замена производных в выражениях (6) и (8) выполнена посредством центральных трехточечных разностей, имеющих второй порядок точности. Значения температуры в фиктивных узлах сетки, лежащих за границами вычислительной области
(j = -1 для T1, j = M l-1+1 для T l-1, j = M l-1-1 для Tl, j = M+1 для TL), выражаются из аппроксимаций уравнений (5) для соответствующих слоев в узлах j = 0, j = M l-1, j = M. Разностная схема имеет вид:
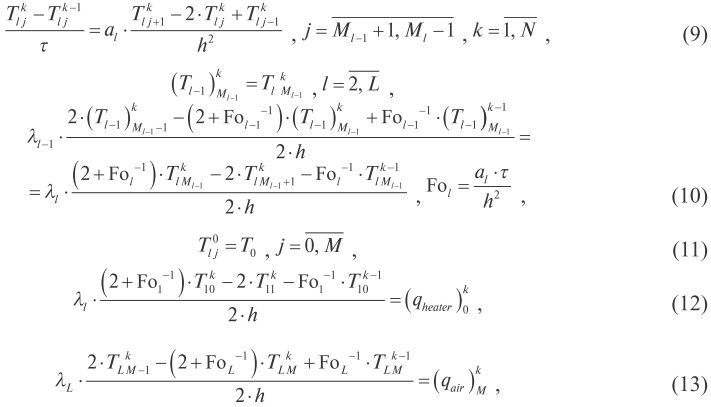
где j, k - номера узлов сетки по толщине и времени; h, τ - шаги сетки по толщине и времени; al - температуропроводность l-го слоя, м2/с; M l-1, Ml - номера граничных узлов l-го слоя; M, N - число шагов сетки по толщине и времени; Fo - число Фурье.
Выражения (12), (13) являются аппроксимациями условий (8а). Разностные аналоги условий (8б), (8в) получаются аналогично.
Система алгебраических уравнений (9)-(13) линеаризуется путем разложения сеточных температур в k-й момент в ряды Тейлора с сохранением линейных членов:
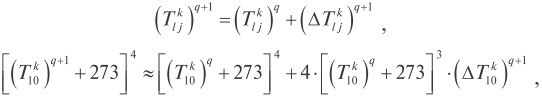
где q - номер итерации; (∆Tlj k)q+1 - поправка к температуре, °С.
Полученная система линейных уравнений для поправок с трехдиагональной матрицей коэффициентов решается на каждой итерации методом прогонки с автоматическим поиском устойчивых шагов по методу половинного деления. Расчет стартовых прогоночных коэффициентов для первого слоя осуществляется по линеаризованному выражению (12), для каждого следующего l-го слоя - по выражению (10). Алгоритм решения описан в работе [1].
Создан гибкий программный комплекс для исследования и управления процессами нагрева слоистых материалов, включающий модули синтеза модели, расчета распределения температуры по толщине и времени, поиска управляющих воздействий по критерию неравномерности температурного профиля, библиотеку моделей методов нагрева, базу данных теплофизических свойств полимерных и текстильных материалов, графический интерфейс исследователя. Структурный синтез осуществляется путем формирования системы уравнений теплопроводности слоев и условий межслоевого контакта по заданной структуре материала и выбора типа граничных условий из библиотеки в зависимости от заданного метода нагрева H. Параметрический синтез заключается в формировании числовых значений параметров модели (теплофизические свойства материалов слоев Sl, характеристики нагревателей и воздуха в цехе) из базы данных (БД) материалов и библиотеки методов нагрева по структуре материала и типу метода нагрева. Алгоритм поиска управляющих воздействий представлен на рис. 2.
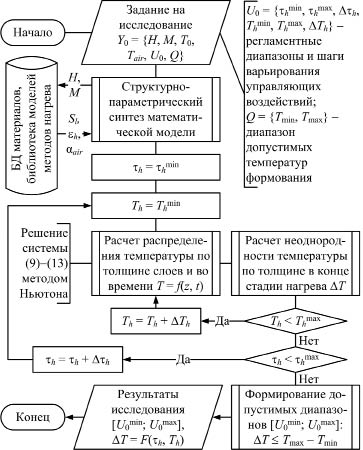
Рис. 2. Алгоритм поиска режимных параметров процесса нагрева
Анализ зависимости показателя неоднородности температуры по толщине от времени нагрева и температуры нагревателей, варьируемых в заданных диапазонах, ∆T = F(τh, Th) позволяет сформировать диапазоны допустимых значений режимных параметров U0min = {τh0min, Th0min}, U0max = {τh0max, Th0max}, при которых неоднородность температуры не превышает заданного значения.
Поле температуры пенополивинилхлорида показано на рис. 3.
Таким образом, разработана математическая модель нагрева слоистых материалов, которая позволяет выбрать управляющие воздействия на процесс по критерию температурной неоднородности для различных методов нагрева, типов и структур материалов.
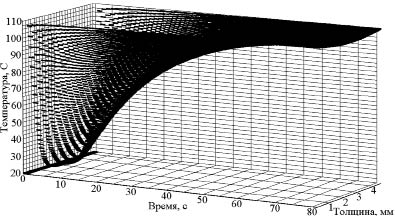
Рис. 3. Распределение температуры по толщине слоя и во времени
Список литературы
- Полосин А.Н., Чистякова Т.Б. // Вестник компьютерных и информационных технологий. 2010. № 10. С. 40.
- Чистякова Т.Б., Полосин А.Н., Гольцева Л.В. Математическое моделирование химико-технологических объектов с распределенными параметрами. - СПб.: Профессия, 2010. -240 с.
- Шерышев М.А. Пневмо-вакуумформование. - СПб.: Профессия, 2010. - 192 с.
- Debergue P. // 58th SPE ANTEC Conf. Proc. Orlando, 2000. Vol. 1.



