Введение
Электронная среда стала неотъемлемой частью образовательного процесса в вузе. Использование тестирования в качестве текущей и промежуточной аттестации, размещение лекционного и практического материала в сети Интернет стало обыденностью для многих вузов [1]. Однако наличие доступа у обучающихся к системам поиска ставит перед преподавателем задачу заинтересовать студента своим предметом настолько, чтобы он сам ограничил возможность использования поисковиков. Однако смысл обучения не в получении правильного ответа, а в формировании у обучающихся способности выявлять сущность проблемы и подбирать для ее решения соответствующий математический аппарат; в развитии у него математической логики, необходимой для формирования суждений по соответствующим проблемам; в знании потенциальных возможностей математических дисциплин в отношении их приложений [2].
Востребованность онлайн-обучения определена пережитыми, но не забытыми периодами самоизоляции из-за пандемии, личными обстоятельствами и т.п. Эти причины побудили вузы включать в обучение дисциплины, проводимые в онлайн-формате, либо полностью переходить на дистанционное обучение. Поэтому приоритетной задачей вузов становится совершенствование образовательной среды в соответствии с передовыми технологиями, внедрение новых форм взаимодействия преподавателя с обучающимися, повышение цифровой компетентности преподавательского состава [3]. На современном этапе развития высшего образования преподаватели должны уметь работать в дистанционном режиме, при необходимости применять информационно-коммуникационные технологии [4].
Грамотно построенный онлайн-курс может не только давать базовые знания по предмету, но и обладает широкими возможностями для углубленного изучения материала по выбранным разделам и в отношении приложений к другим областям. Составление подобного онлайн-курса сопряжено со многими трудностями, поэтому следует учитывать предыдущий опыт работы в этой области [5].
Цель исследования – определение правил и разработка оптимальной структуры онлайн-курса по математической дисциплине.
Материал и методы исследования
Исследование проводилось с использованием следующих эмпирических методов: наблюдение, педагогический эксперимент. В рамках эмпирических методов осуществлялись исследование и анализ результатов, полученных после внедрения в учебный процесс онлайн-курсов по математическим дисциплинам у студентов ФГБОУ ВО «Юго-Западный государственный университет» (далее – ЮЗГУ) по семи направлениям подготовки. Авторами были разработаны и внедрены в образовательный процесс два онлайн-курса – «Алгебра и геометрия» и «Прикладной математический анализ». Курс «Алгебра и геометрия» был введен первым, поэтому курс «Прикладной математический анализ» составлялся с учетом опыта работы с предыдущим курсом. Оба курса имеют общую структуру, включающую инструкции и аннотацию; разделы с видео и презентациями по лекционным и практическим занятиям, при этом в каждом разделе имеются индивидуальные задания для самостоятельной работы и тесты для текущей аттестации, а также промежуточное тестирование. Период исследования – 2023–2025 гг. Логическими методами исследования выступили методы описания, анализа, синтеза, конкретизации, обобщения и др.
Результаты исследования и их обсуждение
Процедура составления онлайн-курса может отличаться из-за учета специфики изучаемого предмета, поэтому в данном исследовании речь пойдет только о математических дисциплинах. Следует отметить еще одну особенность рассматриваемых курсов: каждое лекционное и практическое занятие записывается заранее, ссылка на видеозапись занятия, а также соответствующая презентация размещаются в электронной образовательной среде, а во время пары имеется возможность связываться с педагогом и задавать вопросы. Преподаватель становится сторонним консультантом, одним из источников трансляции знаний, а не ведущим субъектом [6]. Также следует обратить внимание на внутренние требования вуза к системе оценивания. В ЮЗГУ действует балльно-рейтинговая система (далее – БРС), регламентирующая получение студентами очной формы обучения за семестр максимальных 16 баллов за посещаемость, 48 баллов за успеваемость и 36 баллов за промежуточную аттестацию (при зачете или экзамене). Ежемесячно преподаватели должны по своему предмету выставлять аттестацию из расчета максимальных 4 баллов за посещаемость и 12 баллов за успеваемость. Кафедра высшей математики ЮЗГУ обычно работает с контингентом 1-го и 2-го курсов, поэтому семестр длится 18 учебных недель (4-й семестр может сокращаться в связи с практикой). Предметы «Алгебра и геометрия» и «Прикладной математический анализ» читаются в 1-м и 2-м семестрах соответственно, поэтому они оба составлялись из расчета 18 учебных недель. В силу этих причин на первую и последнюю аттестацию приходится по 5 недель, а на вторую и третью – по 4 недели.
В начале формирования онлайн-курса следует тщательно продумать все возможности для набора обучающимися баллов. Для этого необходимо соотнести регламентированные в БРС баллы с видами работ, планируемых к выполнению.
Первой трудностью при составлении онлайн-курса является структурирование курса на разделы. Необходимо учитывать объем изучаемого материала, количество учебных недель и возможности для аттестации в рамках, установленных БРС. В приведенном случае дробление материала должно быть кратно или 4 (есть 4 контрольные точки для проведения аттестации), или 9 (всего 18 учебных недель, можно дать раздел на 2 недели). Дисциплина «Алгебра и геометрия» была переведена в онлайн-формат первой, в ней 9 разделов, но в процессе работы стало понятно, что лучше разделять материал на 8 или 4 раздела под аттестацию, поэтому при формировании курса «Прикладной математический анализ» были внесены коррективы, и он содержал 4 раздела. При этом пришлось соединять смежные разделы, например, раздел 4 называется «Интегральное исчисление. Дифференциальные уравнения», хотя их целесообразнее было бы разделить.
Важность разбивки материала по разделам является спецификой именно математических дисциплин, поскольку нужно учитывать сложность предмета. Видеозаписи лекционных и практических занятий часто просматриваются несколько раз, решение стандартных примеров необходимо записать в тетрадь, на это требуется время. Нужно понимать, что обычный студент не будет сидеть над изучением одного лекционного (или практического) занятия слишком долго. Необходимо рассчитать рациональный объем материала, чтобы его освоение (включая просмотр видео, конспектирование и повторение) укладывалось в 1,5 ч – временной лимит одной пары по расписанию. Это накладывает на составителя курса ограничения в размере основного материала. Например, на изучение интегрального исчисления дается четыре лекционных занятия, это при учете работы и с неопределенными, и с определенными интегралами, и с их приложениями, поэтому невозможно выдать алгоритмы нахождения всех основных видов неопределенных интегралов. В каждой учебной группе студенты имеют разный уровень знаний школьной математики, различные интересы и потребности, поэтому для тех, кто в силу каких-то причин хочет рассмотреть материал глубже, можно включить дополнительные подразделы. Тогда будет дана возможность дифференцированного обучения: все должны изучить основы, но есть возможность разобраться дополнительно на выбор в одном или нескольких приложениях.
Еще одной особенностью математики является то, что важно не знание определений, теорем или формул, а алгоритмов решения задач и упрощенных схем, позволяющих логически прийти к верному ответу. Кроме того, обучающиеся, как правило, предпочитают использовать поисковые системы, а не заучивать материал. Это все исключает возможность проведения только тестирования знаний на каждом занятии. Логично для проверки полученных навыков решения задач выдавать индивидуальные задания. В электронной образовательной среде можно для этого воспользоваться элементом «Задание», тогда решение можно будет прислать в виде файла, или через элемент «Тест» перейти в банк вопросов к заданиям типа «Эссе», тогда ответ загружается либо через введенный текст, либо через файлы (фото, сканы записей от руки и др.). Индивидуальные задания следует выдавать не после каждого занятия, а после проведения двух или трех занятий по схожему разделу. Заданий должно быть немного, лучше 3–4. Большой объем заданий демотивирует студентов, а если их будет приемлемое количество, это позволит получить баллы и отработать навыки решения задач без чрезмерных затрат времени. Тестированием можно завершать каждый раздел. Каждый тест должен содержать различные типы вопросов: открытые, закрытые, на соответствие и др. Подобный вариант курса является оптимальным, поскольку в дисциплине «Алгебра и геометрия» к каждому практическому занятию предлагалось выполнение индивидуальных заданий и тестирования, но обучающиеся не сдавали работы вовремя и с каждым разом задолженность все росла, а на вопросы об успеваемости ответы были практически одинаковыми: «мы не успеваем все вовремя выполнить, у нас нет времени, так как по другим предметам тоже много задают».
Баллы за посещаемость, регламентированные БРС ЮЗГУ, утрачивают свой первоначальный смысл, так как если видео, презентации, индивидуальные задания и тесты уже выложены в электронной среде заранее, то обучающийся может приступить к работе в любой момент. Во время пары по расписанию у него имеется возможность связи с преподавателем и разбора возникающих вопросов. В случае отсутствия вопросов студент может выполнять все задания в любое время до обозначенного преподавателем срока, когда необходимо прикрепить работу или выполнить тестирование. Поэтому баллы за посещаемость могут быть заменены баллами за выполнение индивидуального задания в срок. В курсе алгебры и геометрии после каждого практического занятия, которое проводилось по расписанию раз в две недели, выдавалось по четыре индивидуальных задания (каждое оценивалось в 0,5 балла) и требовалось пройти тестирование. Баллы за индивидуальные задания были засчитаны в категорию «посещаемость», а баллы за тестирование – в категорию «успеваемость». В такой системе оценивания были сложности из-за изначальной разбивки не на 8, а на 9 разделов, поэтому пришлось корректировать количество баллов за работы в последнем разделе. Подобные проблемы были устранены при составлении курса по прикладному математическому анализу – там баллы за посещаемость ставились исходя из указанных преподавателем сроков сдачи работ, а баллы за успеваемость суммировались из баллов за решение индивидуального задания и баллов за тестирование по разделу.
Определив количество разделов и варианты получения баллов за аттестации, нужно предусмотреть действия обучающихся, которые не набрали минимально необходимого числа баллов для выхода на промежуточную аттестацию. БРС ЮЗГУ регламентирует для студентов очной формы обучения получение минимум 24 баллов по успеваемости для допуска к зачету или экзамену. Возможны различные подходы к устранению возникающих проблем с набором баллов: во-первых, можно предоставить возможность отработки индивидуальных заданий и тестов по одному или нескольким разделам, во-вторых, добавить новый раздел «Дополнительные баллы», в котором обучающимся можно будет пройти мини-тестирование по всем изучаемым разделам курса.
Завершается курс тестированием по всем изученным разделам. Общее количество баллов за курс максимально может составить 100, однако есть возможность еще добрать премиальные баллы за дополнительную работу, например за написание статьи, за призовое место на математической олимпиаде и т.п. Сумма всех баллов, полученных обучающимся за четыре аттестации с дополнительными и премиальными баллами, баллами за тестирование дает итоговую оценку (или зачет).
Остановимся теперь подробнее на каждом элементе онлайн-курса по математической дисциплине. Элементы курса должны изучаться последовательно, в порядке их расположения.
В инструкции к курсу описывается информация по срокам сдачи работ, набору баллов, методам контроля, потенциалу снижения или увеличения баллов и т.п. Необходимая информация может дублироваться в описании каждого последующего раздела курса. Как показывает опыт, прочитав раз инструкцию, обучающиеся все равно начинают задавать вопросы, ответы на наиболее часто встречающиеся из них можно дать в описании разделов [7].
Аннотация к курсу должна содержать цель и задачи изучаемой дисциплины, индикаторы компетенций, формируемых при ее изучении, а также перечисление разделов курса.
Каждый раздел курса включает ссылки на видео лекционных и практических занятий, презентации к ним, дополнительные материалы в случае необходимости, например таблицы производных или интегралов, индивидуальные задания и тестовые задания по разделу. Прохождение элементов раздела должно контролироваться. В электронной образовательной среде есть несколько возможностей контроля: автоматический, контроль обучающимся и отдельно преподавателем. Система осуществляет автоматический контроль, например, при просмотре видео занятия. Стоит обучающемуся начать просмотр, как напротив элемента появляется «галочка», свидетельствующая о его прохождении. Студент может самостоятельно себя контролировать, если проставляет «галочку» напротив элемента в случае его прохождения. Такой вариант контроля возможен, например, для презентаций, так как иногда их просмотр необязателен, достаточно изучить материал через видео занятия. Преподаватель может контролировать прохождение элемента раздела, например, при проверке индивидуального задания. Пока не проставлена оценка, элемент не считается выполненным. Также педагог может осуществлять контроль и при тестировании обучающегося, если в тесте есть задания типа «Эссе». Контроль элемента можно убрать, если он не требуется, например если в разделе выложен дополнительный или углубленный материал для отдельных интересующихся.
Отдельно остановимся на видео лекционных и практических занятий и презентациях к ним. Неинтересное видео демотивирует студентов к просмотру последующих материалов, что приводит не к усвоению знаний, а к активному использованию поисковых систем. Видео должно быть информативным, интересным и не должно занимать все отведенные 1,5 ч (академическую пару). Эффективное время просмотра составляет около 30–40 минут, информация должна подаваться с использованием рисунков, схем, анимации и цветового выделения ключевых формул и определений. Это способствует улучшению восприятия задачи и помогает увидеть сходства и отличия аналогичных задач. В свою очередь, формируемые умения (структурировать данные, выделять сущность, видеть общее и различное) позволяют в дальнейшем строить математические модели [8]. Аналогичных принципов следует придерживаться при создании презентаций: в среднем 20–30 слайдов, выполненных в хорошем цветовом оформлении с большим количеством примеров. Использование программы Power Point для построения онлайн-курса может расширить возможности обучения. Индивидуальные задания и вопросы тестов должны дублировать показанные в лекциях или практиках алгоритмы решений. Любое необоснованное усложнение заданий приведет к тому, что обучающийся воспользуется поисковым сервисом, тогда обучение не принесет желаемых результатов. Это одна из особенностей онлайн-обучения, поскольку при живом контакте педагог имеет дополнительные возможности контроля [9].
Неизбежным процессом является уменьшение количества базового материала и переход его части в дополнительный. Каждое направление подготовки или специальность имеют свою специфику. В онлайн-курсе есть необходимость уменьшения базового материала, поэтому имеется несколько возможностей для работы с приложениями математики в профессии обучающегося. Во-первых, можно включать прикладной материал как дополнительный элемент в разделе, таких элементов может быть несколько, их можно разграничить по направлениям подготовки и специальностям, если курс рассчитан на работу с несколькими потоками студентов. Во-вторых, междисциплинарные связи возникают при решении профессионально ориентированных задач, поэтому их нужно включать в индивидуальные задания или тестовые вопросы [10].
Примером математического приложения для экономистов, которое можно дополнительно добавить как к разделу «Системы линейных уравнений» в курсе «Алгебра и геометрия», так и к разделу «Функции нескольких переменных» в курсе «Прикладной математический анализ», может стать нахождение оптимума в задачах линейного программирования. Решение задачи выбора и оптимизации является одной из основных в экономике. Важно распределение ресурсов: куда их направить, чтобы получить максимальную отдачу [11].
Профессионально ориентированные задачи вызывают у студентов значительно больший интерес, чем абстрактные задания из учебников. Последние часто не демонстрируют связь математики с будущей профессией.
При разработке иллюстративных материалов важно закладывать и возможность использования студентами новых образовательных технологий, которые повышают мотивацию и эффективность учебного процесса [12]. Работая над выполнением индивидуального задания, студент может пользоваться различными программными продуктами: например, графики функций для нахождения площади фигуры, ими ограниченной, можно строить с использованием множества программ.
В разделе «Дополнительные баллы» содержится информация о минимальных баллах для допуска к промежуточной аттестации, описывается процедура их получения, дан мини-тест по всем разделам курса.
Доступ к промежуточной аттестации можно ограничить либо с помощью пароля, либо обязательным прохождением перечисленных элементов курса, либо указать дату и время еще на этапе его формирования. Нулевой вариант теста поможет обучающимся лучше подготовиться к зачету или экзамену. В тестирование нужно обязательно включать несколько типов вопросов, таких как: задания в закрытой и открытой формах, вопросы на соответствие и последовательность, задания с числовым или текстовым ответом и т.д. Однако вероятность того, что студент, использующий поисковик, найдет правильный ответ, в таких вопросах велика. Постоянное обновление банка вопросов, использование усложненных вопросов, ограничение по времени – это обязательная часть работы с онлайн-курсом. Профессионально ориентированные задачи также должны присутствовать в тестировании, их можно вводить в банк вопросов через элемент «Эссе». Преподаватель должен будет вручную проверить каждый вопрос такого типа, это дополнительные сложности для педагога, но это возможность убедиться, что студент выполнил работу сам.
На основании проведенного исследования определена оптимальная структура онлайн-курса, ее схема приведена на рисунке [13].
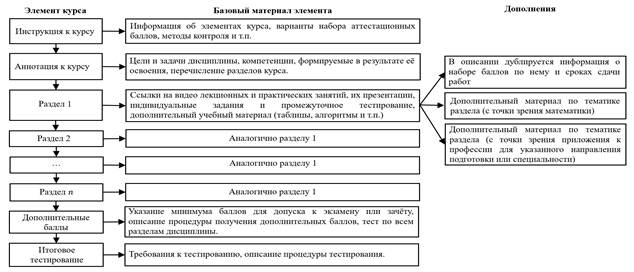
Оптимальная структура онлайн-курса по математической дисциплине
Примечание: составлен авторами по результатам данного исследования
Следует отметить, что в настоящее время накоплено еще недостаточно данных о качестве онлайн-обучения, поскольку массовый переход вузов на этот формат произошел относительно недавно. Министерство науки и высшего образования Российской Федерации осуществляет мониторинг внедрения и использования цифровых технологий в вузах [14]. Очевидно, что технологии мониторинга будут совершенствоваться с появлением и развитием новых инструментов сбора, обработки и анализа данных [15]. В данном исследовании выводы строились на основании конкретной работы с потоками студентов. Преподаватели проводили опросы студентов и при появлении сигналов о каких-то проблемах оперативно вносили изменения в курс. Работа над курсами ведется и в настоящее время.
Подытоживая, сформулируем основные правила построения онлайн-курса по математической дисциплине:
Правило 1. Презентации лекционных и практических занятий необходимо выполнять в разных цветах.
Правило 2. В лекциях обязательно должны присутствовать примеры решения стандартных задач.
Правило 3. В практиках должны быть перечислены основные формулы и алгоритмы решения из теории.
Правило 4. Подбирать комплекс профессионально ориентированных задач, учитывая специфику направления подготовки.
Правило 5. Для устранения пробелов школьных знаний уделять внимание базовым, фундаментальным вещам.
Правило 6. Разбирать несколько типовых вариантов одного вида задач.
Правило 7. Показывать несколько вариантов решения задач.
Правило 8. Алгоритмизировать процесс решения задач.
Правило 9. Давать доступ к дополнительной информации.
Заключение
Проведенное исследование позволило сформулировать методологически обоснованный подход к созданию онлайн-курсов, адаптированных к реалиям современного образования и специфике вузовской системы оценивания. На основе практического опыта реализации курсов «Алгебра и геометрия» и «Прикладной математический анализ» в электронной образовательной среде ЮЗГУ были выявлены ключевые организационные и содержательные проблемы и предложены пути их решения.
Основным результатом работы стала оптимальная структура онлайн-курса, центральным элементом которой стало согласование разделов дисциплины с периодом обучения и балльно-рейтинговой системой вуза. Была предложена эффективная адаптация БРС, в которой баллы за посещаемость трансформируются в баллы за своевременное выполнение индивидуальных заданий, что отвечает асинхронной природе онлайн-обучения. Сформулированные правила и требования к созданию онлайн-курсов направлены на повышение вовлеченности студентов и противодействие формальному выполнению заданий. Важным компонентом мотивации признано включение в курс профессионально ориентированных заданий, наглядно демонстрирующих связь математической дисциплины с будущей профессиональной деятельностью обучающихся.
Таким образом, исследование не только предлагает конкретные, апробированные правила построения онлайн-курсов, но и представляет универсальную логику их построения, учитывающую необходимость баланса между учебной дисциплиной, требованиями системы оценивания, психологией обучающегося и развитием профессиональных компетенций. Полученные результаты обладают потенциалом для экстраполяции и могут служить основой для создания онлайн-курсов по другим дисциплинам.



