Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,039

Введение. Текстовые арифметические задачи составляют основную часть содержания начального курса математики. Именно с их помощью вводится большинство математических понятий в начальной школе, формируется целостное представление об окружающем мире, развиваются мыслительные операции.

Одна из ключевых задач начального обучения математике – научить детей решать текстовые задачи. Это один из самых сложных вопросов в начальном курсе математики. Федеральный институт педагогических измерений, оценивая результаты ЕГЭ по математике, указывает на то, что несформированность умений анализировать условие задачи и составлять математическую модель является препятствием для успешного решения практико-ориентированных задач, что снижает общую математическую компетентность выпускников. [1].

Во ФГОС НОО определены умения, которыми необходимо овладеть обучающимся в результате изучения учебного предмета «Математика»: «решать текстовые задачи; иметь опыт работы с информацией, представленной в графической и текстовой форме: умения извлекать, анализировать, использовать информацию и делать выводы; использовать начальные математические знания при решении учебных и практических задач и в повседневных ситуациях» [2, с. 37-38]. Умение решать текстовые задачи включает как предметные, так и метапредметные действия в своем составе, что впоследствии помогает обучающимся в решении любых бытовых и профессиональных задач.

На протяжении веков проблема обучения решению текстовых задач остается актуальной. Процесс обучения младших школьников решению задачи в современной школе в большинстве случаев строится на заучивании ключевых слов для определенного вида задач и выстраивании на их основе алгоритма решения. Этот способ обучения не позволяет большинству обучающихся решать любую практико-ориентированную задачу, потому что её контекст отличается от «стандартного» по форме представления или семантической структуре, а общий прием решения текстовой задачи остается не сформированным.

По мнению авторов, традиционный подход к решению задач не обеспечивает одинаково успешного результата для всех обучающихся. Причина кроется в индивидуальных психологических особенностях учащихся и различиях в их исходных знаниях и умениях, которые являются фундаментом для формирования умений решения текстовых задач. Младшие школьники, имеющие разную степень обученности, к процессу решения задачи подходят по-разному, что не всегда учитывается педагогом при организации учебно-познавательной деятельности. Авторы считают целесообразным при организации деятельности младших школьников в работе с текстовой задачей использовать разные методические приемы в соответствии с их уровнем обученности, что будет способствовать формированию умений решать задачи у всех обучающихся.

Цель исследования – на основе теоретического анализа выделить и описать методические приемы обучения младших школьников решению текстовых задач, выделить условия их применения для обучающихся с разным уровнем обученности.

Материал и методы исследования

Основными методами исследования выступали теоретические (анализ научной и психолого-педагогической литературы) и эмпирические (тестирование, анализ продуктов деятельности обучающихся). Эмпирические методы исследования позволили определить уровень обученности младших школьников в области умения решать текстовые задачи. Исследование проходило на базе муниципального бюджетного общеобразовательного учреждения «Центр образования №9 им. генерала А.Н.Ермакова» г. Тула в течение 2022–2024 годов, участниками были обучающиеся 3-4 классов в количестве 56 человек (29 человек – экспериментальный класс, 27 человек – контрольный класс).

На основе методики Н.Б.Истоминой определяли сформированность умений выделять условия и требования, устанавливать отношения и зависимости между искомыми и известными объектами [3, с. 238]. Модифицированная методика А.Н.Рябинкиной [4, с. 114] использовалась для оценки сформированности у младших школьников умения составлять математическую модель к задаче.

Диагностика сформированности умения решать задачи, основанная на методике А.Р.Лурии и Л.С.Цветковой [4, с. 112], проводилась с целью выявления уровня сформированности умения действовать в стандартной, незнакомой и нестандартной ситуациях.

В ходе педагогического эксперимента для организации активной учебно-познавательной деятельности обучающихся по работе с текстовой задачей на уроках математики авторы использовали специальные обучающие задания, основанные на разных методических приемах. Для более продуктивного формирования умения решать текстовые задачи были заимствованы методические подходы Н.Б.Истоминой, включающие сравнение, выбор, преобразование и конструирование [3, с. 236–237].

Результаты исследования и их обсуждение

Текстовые задачи в начальном курсе математики представляют собой описание конкретного события или процесса объективной реальности, представленных в основном на естественном языке. Вместе с тем увеличивается и число задач, предъявляемых в виде таблицы, графика, рисунка и др. Это влечет за собой необходимость формирования у младших школьников обобщенного умения решать задачу, не соотнося ее с определенным типом.

Авторы, вслед за А.В. Белошистой, рассматривают решение задачи как умение перевести словесное описание ситуации в математическую форму. Чтобы успешно это сделать, младший школьник должен хорошо понимать и анализировать структуру текста задачи [5, с. 6].

Решение задачи в традиционной методике обучения определяется как раскрытие связи между данными условиями задачи и искомым, на основе чего выбираются, а затем выполняются арифметические действия и дается ответ на вопрос задачи. Приемы организации фронтальной работы учителя с обучающимися по решению задач представлены в работе С.Е.Царевой, где выделяются приемы работы, связанные с формированием действий сравнения, сопоставления и анализа [6], что, по мнению авторов, более эффективно для формирования общего приема решения текстовых задач.

Обучение общему приему решения текстовой арифметической задачи является приоритетным в развивающих системах обучения Л.В.Занкова и Д.Б.Эльконина–В.В.Давыдова, поскольку позволяет научить младших школьников решать любые виды задач, в том числе и повышенной трудности. При данном подходе выделяются два этапа обучения: подготовительный и основной. Цель первого – формирование логических действий, на втором этапе происходит овладение общими умениями решения текстовых задач [7], что совпадает с позицией авторов по данному вопросу.

Вместе с тем умение решать текстовые задачи опирается на сформированные у младшего школьника познавательные универсальные учебные действия, такие как анализ, моделирование, преобразование информации из одной формы в другую, кодирование и декодирование информации. Эти действия, с одной стороны, входят в деятельность моделирования, а с другой - являются этапами решения текстовой задачи. Поэтому учебное моделирование, описанное в исследовании Н.В.Буренковой [8], авторы применяют на всех этапах в ходе обучения решению задачи.

Ученые выделяют разные методические приемы обучения младших школьников решению текстовых задач, однако нет общепринятой классификации и рекомендаций по их использованию. А.К.Мендыгалиева и Т.В.Хисматулина описывают методику применения приемов, связанных с составлением текста задачи [9], О.И.Митюк исследует потенциал графического моделирования в формировании навыков решения текстовых задач [10], И.Н.Кваша проводит систематизацию методических приемов, соотнеся их с конкретными этапами решения текстовых задач [11].

При формировании обобщенного умения решения текстовой задачи авторы уделяют особое внимание формированию каждого действия в его составе, используя на этапе моделирования приемы, предложенные О.В.Бахтиной, чтобы обучающиеся с разной степенью обученности приобретали навыки решения любой задачи [12]. Первым шагом в овладении умением решать текстовую задачу является работа с текстом, анализ текста задачи, который организуется с помощью таких приемов, как выделение главных слов, удаление слов, несущественных для решения задачи, выбор или постановка вопроса. Для визуализации информации при реализации этих приемов используется интерактивная доска, которая позволяет превратить овладение действием анализа текста в интерактивную игру [13].

Работа с текстом включает семантический и математический анализы текстов задач. В.В.Кокорева с соавторами выделяет этапы смыслового чтения для осознания младшими школьниками смысловой символики, специфического языка и логической структуры текста задачи [14]. Г.Н.Кимаковская говорит о необходимости обучения переводу текста с естественного языка на математический, используя при этом предварительный анализ, взаимно-обратный перевод, перевод сначала на абстрактный уровень естественного языка [15]. В.А.Цыбикова, исследуя приемы анализа текста задачи, выделяет приемы синонимическая замена и пересказ текста для усвоения смысловой структуры текста [16].

Одним из эффективных приемов на данном этапе выступает и функциональное чтение, позволяющее овладеть умениями извлекать из текста только ту информацию, которая необходима для решения конкретной задачи или ответа на конкретный вопрос. При реализации этого приема обучающиеся получают задания, связанные:

– с поиском информации. Например, «На рисунке 1 отражено количество обучающихся начальных классов. В каких классах одинаковое число обучающихся? На сколько человек во втором классе больше, чем в четвертом классе?».

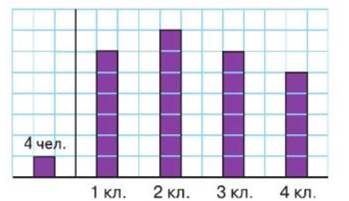
Рис. 1. Задание для обучающихся, где нужно определять количество обучающихся в классах, сравнивать число детей в разных классах [17, с. 16]

Поиск информации в данном задании связан не только с определением высоты столбцов, но и с выяснением числа людей, которые соответствуют заданному количеству клеток;

– с пониманием прочитанного. Например, «Из двух городов Твери и Ржева по Волге навстречу друг другу вышли два теплохода. Первый прошел до встречи 82 км, второй – 98 км. Определите длину Волги между этими городами». В данном контексте задачи обучающимся необходимо увидеть, что длина реки совпадает с расстоянием, которое проходят теплоходы;

– с интерпретацией информации. Например, задание для обучающихся «Перед вами, в таблице 1, расписание движения поезда Белгород – Москва. Пользуясь им, определите, между какими населенными пунктами самое большое (маленькое) расстояние, если считать, что поезд движется все время с одинаковой скоростью. Сколько времени затратил поезд на путь от Орла до Тулы?»;

Таблица 1

Расписание «Поезд “Ласточка” 746В Белгород – Москва»

Примечание: составлено авторами по материалам официального сайта РЖД.

– с применением информации для решения своей задачи. Например, задание для обучающихся «Используя расписание движения поездов с Московского вокзала г. Тулы в сторону Москвы (табл. 2), определите, на каком поезде вы быстрее всего доедете до Москвы».

Таблица 2

Расписание поездов в направлении Москвы

Примечание: составлено авторами по материалам официального сайта РЖД.

Пример другого задания для обучающихся, которое выполняется с использованием таблицы 2: «Вы с родителями оправляетесь на соревнования в г. Минск. Из Москвы ваш поезд отправляется в 20 ч 30 мин. Выберите поезд, на котором вы поедете до Москвы. Рассчитайте, во сколько вам необходимо выйти из дома, если до Московского вокзала вы будете добираться в течение 30 минут и приехать на вокзал вам необходимо за 15 минут до отправления поезда».

Другим эффективным приемом, который используется на первом этапе, является перефразирование текста задачи. Этот прием состоит в том, чтобы, сохраняя качественные аспекты и взаимозависимости, заменить исходную ситуацию на другую, более ярко демонстрирующую суть и связи между величинами [13].

При организации обучения решению текстовых задач учителю необходимо опираться на развитие когнитивных способностей младших школьников, характеризующих уровень их обученности. В педагогическом словаре «обученность – результат обучения (организованного или стихийного), включающий как наличный, имеющийся к сегодняшнему дню запас знаний, так и сложившиеся способы и приемы их приобретения (умение учиться)» [18, с. 97].

Диагностический этап исследования показал, что 42% обучающихся экспериментального класса имеют низкий уровень обученности, 42% – средний уровень и только 16% – высокий. Среди основных ошибок, которые допустили младшие школьники, авторы отмечают: неумение устанавливать отношения между данными и искомым, моделирование условия текстовой задачи, осуществление проверки решения задачи. Анализ полученных результатов свидетельствует о недостаточном уровне сформированности у обучающихся умения решать текстовые задачи, а также существует потребность в поиске методических приёмов, способствующих решению выявленной проблемы.

При организации работы с обучающимися, имеющими низкий уровень обученности, на этапе анализа текста нового вида задач с целью обучения установлению причинно-следственных связей между данными и искомым использовался прием сравнения. Работа сначала проходила совместно с учителем, а затем младшие школьники осуществляли эту деятельность самостоятельно. Постепенно для этой группы подключался прием выбора и задания с комбинацией этих приемов. При этом с помощью приема выбора осуществлялось обучение моделированию текста задачи и определению необходимых арифметических операций. Задания, спроектированные на основе приема выбора, способствовали тому, что обучающиеся могли выявлять значение чисел в условиях задачи, связывать известные данные с тем, что требуется найти, превращать словесные описания в схемы, а также сопоставлять исходную формулировку задачи с предоставленным способом решения.

Работа по интерпретации текста задачи, выбору арифметического действия для решения задачи, с группой обучающихся, имеющих средний уровень обученности, были осуществлены посредством приема преобразования. Этот прием способствовал осознанию причинно-следственных связей между изучаемыми понятиями и обобщенными способами действий. Применяя приём конструирования, авторы стремились сформировать у младших школьников глубокое понимание того, как самостоятельно устанавливать соответствия между предметными, графическими и символическими моделями и преобразовывать их в математические. С его помощью обучающиеся осваивали умения структурировать, анализировать и интерпретировать данные, создавая математическую модель ситуации.

После реализации методических приемов авторы еще раз замерили степень обученности младших школьников решению текстовых задач. Низкий уровень обученности был отмечен у 17% обучающихся, у 46% – средний уровень, у 37% – высокий (рис. 2).

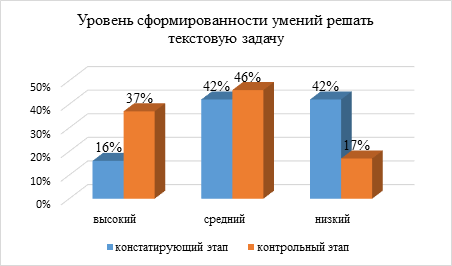
Рис. 2. Сформированность умений решать текстовую задачу у обучающихся экспериментального класса (составлено авторами по результатам данного исследования)

На уроках математики в течение учебного года были предложены задания, учитывающие особенности каждой группы обучающихся. Это позволило всем младшим школьникам последовательно развивать отдельные составляющие умения решения текстовых задач более высокого уровня. Полученные результаты свидетельствуют о положительной динамике формирования у младших школьников умения решать текстовые задачи, что подтверждает эффективность выбранных методических приемов для различных групп обучающихся.

Заключение. Таким образом, если учитель в процессе обучения младших школьников решению текстовых задач использует соответствующие степени их обученности методические приемы, будет выполнена одна из ключевых задач обучения математике – научить школьников решать текстовые задачи.

Для этого авторы предлагают:

–приемы сравнения и выбора в большей степени использовать при работе с младшими школьниками I степени обученности. Эти обучающиеся при решении задачи действуют на уровне памяти, способны воспроизводить заученные действия;

–прием конструирования – при работе с младшими школьниками II степени обученности. Данная группа обучающихся свободно применяет знания для решения «знакомых» задач, а в незнакомой ситуации действует по образцу;

–прием преобразования – с младшими школьниками III степени обученности. Эти обучающиеся владеют общим приемом решения текстовых задач. Они применяют знания в незнакомой ситуации и при решении задач повышенной трудности.

Перспективы развития темы исследования связаны с расширением спектра методических приемов обучения младших школьников решению текстовых задач, разработкой сборника заданий и методических рекомендаций для учителей.