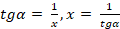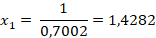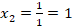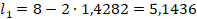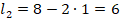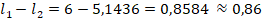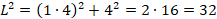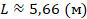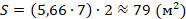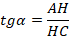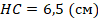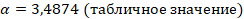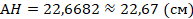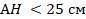Введение
С введением обновленных Федеральных государственных образовательных стандартов в процесс преподавания практически всех предметов вошло понятие функциональной грамотности. В федеральных рабочих программах учебного предмета «Математика» заложены виды деятельности, направленные на формирование читательской, математической и частично естественно-научной грамотностей. С 2018 года действует федеральный проект «Мониторинг формирования функциональной грамотности», направленный на поддержку и обеспечение «формирования функциональной грамотности на основе идей формирующего оценивания» [1, c.16], ежегодно проводятся межпредметные региональные диагностические работы. Однако, как показывает опыт, у большинства учителей понимание отличия, в частности, математической грамотности от чисто предметной подготовки до сих пор не сложилось. На этот факт также обращают внимание специалисты проекта «Мониторинг формирования функциональной грамотности», указывая на то, что «часть учителей закрыта для восприятия новых подходов формирования функциональной грамотности и, как правило, недооценивает возможности детей», и что «важно обратить внимание учителей на нецелесообразность тренировки обучающихся на выполнение отдельных типов заданий и на выучивание способов решения» [1, c.30]. Это «натаскивание» говорит о том, что разницу между заданиями ГИА и мониторинга функциональной грамотности учителя не видят. На взгляд автора, часть этой проблемы состоит в том, что результаты мониторингов школы получают в виде некоторого обобщенного показателя – уровней сформированности функциональной грамотности школьников по городским округам. Автор считает, что более полезной для учителя была бы информация о выполненных и невыполненных их учениками заданиях, об уровнях сложности этих заданий и о том, из чего эта сложность складывается.
Цель исследования
Таким образом, в основу данного исследования был положен вопрос о том, какие затруднения учеников приводят к их низким результатам: низкая функциональная грамотность (читательская грамотность, мыслительные действия, способность удерживать задачу) или сложность математического аппарата.
Материал и методы исследования
Для получения ответа на этот вопрос были использованы материалы заданий и отчетов Федерального мониторинга формирования функциональной грамотности учащихся 8 классов, проводившегося 13.02.–03.03.2023 (9903 учащихся), и метапредметной диагностической работы учащихся Московской области 10-х классов, проводившейся 05.12–14.12.2023 (30037учащихся).
Стартовая диагностика федерального мониторинга функциональной грамотности учащихся 8-х классов выявила такие дефициты математической грамотности (процент выполнения менее 50%), как «применять базовые тригонометрические соотношения для вычисления сторон прямоугольных треугольников» и «анализировать график реального процесса, строить аппроксимации». В качестве материала для исследования были взяты задания, направленные на проверку компетенции «применять базовые тригонометрические соотношения для вычисления сторон прямоугольных треугольников», выявившие самые низкие показатели сформированности данной компетенции.
На проверку данной компетенции было направлено задание «Мансарда».
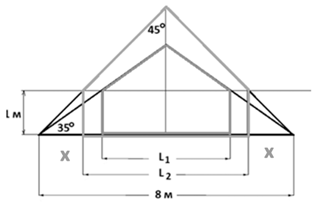
Двускатная крыша – крыша с двумя наклонными плоскостями, расположенными под углом друг к другу. Под такой крышей можно оборудовать мансарду. Чем круче двускатная крыша, тем больше пространство мансарды, которое можно использовать под жилое помещение, однако площадь крыши, а значит и ее стоимость, тоже больше. Поэтому стоит подобрать оптимальное значение угла наклона ската крыши на этапе ее проектирования. Основой конструкции крыши является треугольник. Угол наклона ската крыши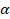 
определяется по законам геометрии треугольника. Из прямоугольного треугольника АВС находим, что 
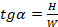(рис. 1).
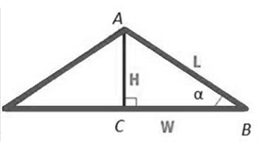
Рис. 1. Чертеж к заданию «Мансарда»
Двускатная крыша является пологой, если угол наклона ската меньше 30°, и крутой, если угол больше 30°.
Замечание: тангенсы углов от 20° до 50° даны таблично.
Вопрос 1. Чтобы под крышей можно было сделать жилое помещение, необходимо, чтобы высота H ската была не менее 2 метров. Планируемая ширина дома составляет 8 м, а угол наклона крыши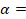 
30°. Возможно ли устроить жилое помещение под крышей такого дома?
Решение.
,
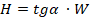где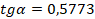 
– табличное значение;
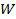
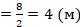– половина ширины дома.
H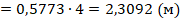 
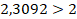
Ответ: поместится.
С заданием, требующим всего лишь подставить в готовую формулу данные, напрямую заданные в условии задачи и табличных данных, и сделать вывод, справилось чуть менее 40% восьмиклассников.
Вопрос 2. Ширина дома – 8 м. Решено, что высота боковых стен будет равна 1 м. Чем круче крыша, тем больше ширина комнаты, которую можно обустроить в мансарде. Сравните ширину комнаты при углах наклона ската крыши, равных 35° и 45° (рис. 2). На сколько метров ширина комнаты во втором случае будет больше?
Решение.
|
Пусть х – половина разницы между шириной мансарды и шириной дома (рис. 2). Тогда
Ответ: 0,86 м. |
|
В данном случае необходимо знание определения понятия тангенса угла прямоугольного треугольника и умение построить простую математическую модель – выделить на чертеже необходимый для решения прямоугольный треугольник и подставить в формулу тангенса данные для этого треугольника. С заданием справилось только около 15% восьмиклассников.
Вопрос 3. Ширина дома – 8 м, длина – 7 м, угол наклона ската крыши – 45°. Чтобы заказать кровельные материалы, необходимо знать площадь всей крыши. Сделайте необходимые расчеты (в м2) и вычислите площадь всей крыши.
Решение.
|
По теореме Пифагора:
Ответ: 79 м2. |
|
Необходимый математический аппарат – теорема Пифагора и формула площади прямоугольника. С применением теоремы Пифагора для поиска недостающего значения одной из сторон прямоугольника и дальнейшего применения формулы площади прямоугольника справилось чуть больше 40% восьмиклассников.
Несмотря на то, что все три вопроса задания «Мансарда» относятся к теме «Теорема Пифагора и начала тригонометрии» федеральной рабочей программы основного общего образования «Математика (базовый уровень)» [2], которая согласно тематическому планированию должна быть изучена на момент мониторинга всеми восьмиклассниками, низкие результаты частично аргументировались тем, что материал был частью школьников только что пройден, а частью – не пройден вовсе.
Если проблема низких результатов действительно в неотработанности предметного материала, то задание на применение этого же математического аппарата учащиеся 10-го класса должны выполнить намного лучше. Вопрос исследования был поставлен следующим образом: смогут ли учащиеся, изучившие данный материал два года назад и имевшие возможность глубокой его отработки в рамках учебного процесса и в повседневной жизни, продемонстрировать более высокий уровень выполнения аналогичных заданий математической грамотности.
Для проверки данной гипотезы в региональный мониторинг математической грамотности учащихся 10-х классов Московской области в рамках региональной метапредметной диагностической работы, проводившейся в том же 2023 году, было включено задание на проверку способности применить такой же математический аппарат в контексте похожей жизненной ситуации.
Задание «Юный орнитолог».
Вопрос 3.
|
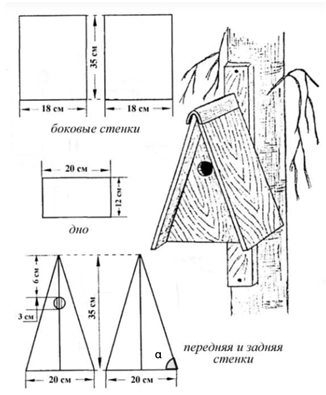
Андрей решил сделать свой домик для птиц в технологии «А-фрейм». Он нашел в интернете чертеж такого домика с прямоугольным дном, но свой домик хочет сделать с квадратным дном (размером 13х13 см) и углом наклона между крышей и дном (угол Рассчитайте высоту домика с новыми данными и ответьте на вопрос. Можно ли внести в чертеж такое изменение, если рекомендуемая высота домика для домового воробья должна находиться в пределах 25–30 см? Замечание: тангенсы углов от 60° до 90° даны таблично. |
|
Решение.
|
В треугольнике HAC:
Высота не лежит в рекомендуемых пределах, следовательно, такие изменения внести нельзя. |
|
Задание требует использования того же математического аппарата: знания определения понятия тангенса острого угла прямоугольного треугольника, умения построить простую математическую модель – выделить на чертеже необходимый для решения прямоугольный треугольник, и подставить в формулу тангенса данные для этого треугольника, сообщенные в прямом виде в условии задачи и табличных значениях, умение сделать вывод.
С полноценным решением этого задания справилось 18% участвовавших в мониторинге десятиклассников, еще 15,5% не смогли привести корректные пояснения. Не справились с заданием 66,5% десятиклассников.
Результаты исследования и их обсуждение
В рамках стартовой диагностики федерального мониторинга 15% восьмиклассников ответили на все вопросы задания «Мансарда» и, таким образом, продемонстрировали все нижеперечисленные знания и умения:
- знание определения понятия тангенса острого угла прямоугольного треугольника;
- умение найти в текстах, включающих чертежи, графики, диаграммы и пр., необходимую информацию;
- умение подставить найденную информацию в имеющуюся формулу;
- умение выразить из формулы требуемую величину;
- умение построить (выделить на имеющемся чертеже) простую математическую модель – конкретный прямоугольный треугольник;
- умение сделать вывод.
В рамках выполнения задания регионального мониторинга, направленного на проверку всех вышеперечисленных знаний и умений, полное выполнение задания продемонстрировало 18% десятиклассников.
По результатам эксперимента можно сделать вывод о том, что успешность использования одного и того же математического аппарата в решении заданий математической грамотности практически не зависит от того, как давно данный аппарат был изучен: только что или два года назад.
Автор считает, что основные дефициты математической грамотности относятся не к предметным знаниям (компетенция «применять»), а к метапредметным компетенциям «формулировать» и «интерпретировать, использовать и оценивать».
Приведем несколько примеров.
Замечание: значение длин сторон и величин углов в представленных решениях могут отличаться в зависимости от номера варианта.
Пример 1 (рис. 2–3).
Рис. 2. Решение ученика 1
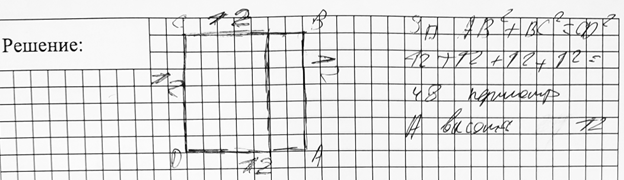
Рис. 3. Решение ученика 2
Решения учеников показывают, что они не разобрались ни с условием, ни с требованием задачи.
Пример 2 (рис. 4–7).
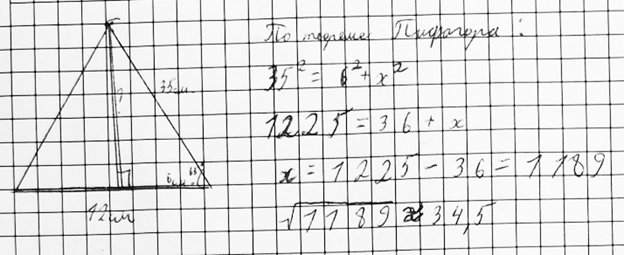
Рис. 4. Решение ученика 3
Рис. 5. Решение ученика 4
Рис. 6. Решение ученика 5
Рис. 7. Решение ученика 6
В этих примерах, увидев на чертеже прямоугольный треугольник, учащиеся пытаются применить теорему Пифагора, несмотря на отсутствие в условии задачи длины гипотенузы и наличие значения тангенса угла .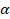
Приведенные примеры демонстрируют дефициты умений:
- создавать математическую модель, отражающую особенности описанной ситуации компетенции «формулировать»;
- размышлять над математическим решением или результатами и переводить математическое решение в контекст реальной проблемы компетенции «интерпретировать, использовать и оценивать».
На взгляд автора, эти же проблемы, а не отсутствие владения десятиклассниками определением понятия тангенса острого угла прямоугольного треугольника являются причиной результата «не приступал к решению».
Таким образом, в процессе оценки уровня сформированности функциональной грамотности ученики любого возраста в основе своей демонстрируют отсутствие сформированности знаний и умений: распознавать проблемы, возникающие в окружающей действительности, которые могут быть решены математическими средствами; формулировать проблемы на математическом языке; анализировать информацию, представленную в различных формах (текст, таблицы, рисунки, чертежи); интерпретировать полученные результаты с учетом поставленной проблемы, формулировать и записывать окончательные результаты решения поставленной проблемы. Также, как показал эксперимент, многие обучающиеся испытывают серьезные затруднения при вычленении и удерживании в процессе решения задачи необходимой информации из текста, таблиц, диаграмм, схем и пр., а особую трудность для обучающихся представляет извлечение информации из нескольких текстов.
Стоит отметить, что эти же проблемы проявляются и у учителей математики Московской области. Так, согласно данным регионального исследования компетенций учителей Московской области, учителя математики показывают низкие результаты не в предметной части, а в области читательской и математической грамотности.
На наличие вышеперечисленных проблем указывают и другие исследования. В публикациях можно встретить выводы о том, что формирование функциональной математической грамотности является «одной из актуальных проблем методики обучения математике», так как сильной стороной наших школьников «является овладение предметными знаниями на уровне их воспроизведения или применения в знакомой учебной ситуации, но у них возникают трудности в применении этих знаний в ситуациях незнакомых, приближенных к жизненным» [1, c.14], «в рамках школьного курса математики учащиеся знакомятся с теорией, приобретают навыки решения задач, построения графиков и т. д… при этом они не способны применять математику для проблемной ситуации, возникающей в обыденной деятельности», «отдельные учебные задачи способствуют формированию и закреплению конкретных навыков (например, решение уравнений) и способствуют элементарной грамотности учащихся, а не функциональной» [3]. Есть данные о том, что российские школьники в рамках исследований математической грамотности стабильно показывают низкие результаты (от 15% до 53%) при выполнении заданий на поиск закономерностей, которые «проверяют умение проводить рассуждения, ответы на вопросы, поставленные в этих заданиях, предполагают наличие у учащихся определенного стиля мышления, при котором ученик ориентирован на наблюдение, выдвижение гипотезы, организацию проверки, обоснование вывода и пр.» [4, c. 96]. Подтверждается отнесение математической грамотности к интеллектуальным способностям, которое «не позволяет рассматривать в качестве математической грамотности заученные механически навыки решения типовых задач и тем более механические навыки оперирования с математическими знаковыми средствами» [5, c.36]. Подчеркивается, что «переход от исходной задачи к математической не является прямым, а опосредуется схематизацией» и «именно этот элемент в структуре математической грамотности в нашем образовании "провален"» [5, c.38].
Решение части представленной проблемы на настоящий момент заложено в тематическом планировании федеральных рабочих программ учебного предмета «Математика». В рамках изучения разделов (тем) курса заложена деятельность по формированию отдельных элементов функциональной грамотности (в ходе изучения предмета): формирование читательской грамотности, мыслительных действий (классификация, анализ, синтез, оценка и пр.), способности удерживать задачу. В рамках изучения раздела «повторение и обобщение» каждого курса заложена деятельность по формированию отдельных элементов функциональной грамотности без привязки напрямую к изучаемому материалу.
Проблемным местом остается соединение этих элементов в собственно функциональную грамотность, которая должна строиться на содержании различных предметов (межпредметных связях) и заданиях, построенных на ситуациях, выходящих за рамки обычных житейских и/или учебных.
Решение этой задачи находится уже на усмотрении учителя и образовательной организации. В научных трудах можно найти следующие предложения.
Первое направление – это использование любых возможностей для обучения учащихся полноценному методу математического моделирования: «учить математическому моделированию реальных ситуаций и переносить способы решения учебных задач на реальные, создавать опыт поиска путей решения жизненных задач» [6, c.129]; решение «задач междисциплинарного, прикладного характера… позволяющих демонстрировать применения математического аппарата для описания реальных объектов и процессов», в результате чего «обучающийся вырабатывает умение работать с математическим текстом, легче переводит на математический язык описание объектов и процессов, правильно интерпретирует полученный результат» [7, c.44].
Второе направление – максимальное использование межпредметных связей: использовать «интегрированные уроки, на которых рассматриваются ситуации по применению математических знаний в рамках других научных дисциплин» [3].
Третье направление – доработка учебников математики: «включение заданий по формированию математической грамотности в учебники… например, каждый раздел математики должен сопровождаться кейс-заданием» [3].
Четвертое направление – использование возможностей внеурочной деятельности: «развивать математическую грамотность не только в урочной деятельности», используя «внеурочное занятие в виде деловой игры», «интегрированные уроки, на которых рассматриваются ситуации по применению математических знаний в рамках других научных дисциплин», использование элективных курсов с акцентом «на самостоятельную деятельность учащихся», где «через составление своих задач, подготовку докладов, ведение проекта школьники осознают возможности математики и приобретают функциональную грамотность» [3].
Выводы
Проведенный эксперимент и обсуждение его результатов позволяют сделать следующие выводы:
- с заданием, решающимся одним и тем же математическим аппаратом, только что изучившие его восьмиклассники и давно применяющие десятиклассники справились одинаково плохо;
- решения учеников демонстрируют:
- низкую сформированность или не сформированность вовсе всех ключевых компонентов функциональной грамотности: низкую читательскую грамотность, слабо сформированные мыслительные действия, неспособность удерживать задачу;
- признаки попыток применения выученных способов решения при виде типовых математических моделей отдельных типов заданий и на выучивание способов решения;
- для достижения желаемых результатов к деятельности по формированию функциональной грамотности учащихся должны подключиться все без исключения участники образовательного процесса.