Современное интенсивно меняющееся промышленное производство требует соответствующей подготовки инженерных кадров, обладающих определенным набором компетенций, способных успешно разрешать различные проблемы, связанные с профессиональной деятельностью. Востребованы не только инженеры, которые легко включаются в технологический процесс, но и все больше возникает потребность в инженерах, способных увидеть существующую проблему, предложить ее решение и реализовать его. Кроме того, все больше технологий становятся мультидисциплинарными.
Одна из основных компетенций современного инженера – способность адаптироваться к возрастающим требованиям в области современной техники, в области новых технологий и программных продуктов. Реализация компетентностного подхода в высшем образовании требует обеспечения качественного математического образования для достижения необходимого уровня математической подготовленности выпускников технических и технологических вузов. Анализ потребностей промышленности и науки показал, что часть учебных программ курса высшей математики не соответствует этим выдвигаемым требованиям. Возникла необходимость пересмотра содержания курса высшей математики с целью учета потребностей студентов и выпускников вузов в математических знаниях. При этом единого механизма своевременного обновления содержания обучения пока нет.
Одной из стратегических мер подготовки современного инженера является реализация междисциплинарного подхода при изучении высшей математики. А именно, будущих инженеров нужно обеспечить более широкой базой знаний, которая позволит им решать сложные мультидисциплинарные инженерные задачи. Необходимыми для решения этой проблемы являются осуществление междисциплинарного взаимодействия между инженерными специальностями и экономикой, программами, объединяющими специализацию в естественных науках и специализацию в менеджменте, наличие междисциплинарного проектирования [1].
Цель исследования. Исходя из действующих ФГОС ВО содержание разделов курса высшей математики в технологическом университете определяется самим вузом с опорой на примерные образовательные программы. Безусловно, подобная самостоятельность высшего учебного заведения как составителя рабочей программы может только приветствоваться, так как такой подход позволяет своевременно обновлять содержание курса в соответствии с основными профессиональными образовательными программами. Но сложно добиться достойного уровня достижения предусмотренных ФГОС образовательных результатов в условиях, когда значительное время на изучение дисциплины перераспределено на самостоятельную работу студентов.
Попытки проектирования содержания дисциплины «Математика» для технических направлений подготовки предпринимались некоторыми авторами [2]. В качестве критерия, позволяющего отобрать необходимый учебный материал, ими был предложен метод матриц логических связей [3].
Целью нашего исследования является проведение обоснованной дифференциации изучаемого материала дисциплины «Математика» для технологических направлений подготовки.
Дифференциация содержания курса высшей математики была рассмотрена для направления 18.03.01 «Химическая технология» – одного из основных направлений обучения в технологическом университете. Государственный стандарт для подготовки бакалавров данного направления выдвигает задачу формирования такой компетентности, как готовность применять аналитические и численные методы решения поставленных профессиональных задач. В условиях сокращения объема часов, выделенных на изучение дисциплины, необходимо сохранить целостность, глубину и системность в понимании методов и приемов современной математики [4].
При подготовке бакалавров направления 18.03.01 для набора 2019 г. на дисциплину «Математика» выделено 12 зачетных единиц (и 3 зачетные единицы – на контроль усвоенных знаний), 21% от общего объема часов выделен на лекции, 31% – на практические занятия и 48% – на самостоятельную работу студентов.
Индикаторы достижения общеобразовательных компетенций ООП предписывают для выпускников усвоение знаний элементов дифференциального, интегрального исчислений, элементов дифференциальных уравнений, теории вероятностей и математической статистики. Современный инженер должен иметь представление об основных современных математических теориях и методах, заложенных в основу различных математических моделей. Он обязан уметь применять полученные математические знания, методы и навыки для решения типовых профессиональных задач.
Анализ содержания междисциплинарных связей дает возможность выявить темы программы дисциплины «Математика», на усвоение содержания которых опирается учебный материал большей части профильных дисциплин данного направления. Ниже приведены профильные дисциплины направления «Химическая технология», использующие элементы курса высшей математики (рисунок).
МАТЕМАТИКА
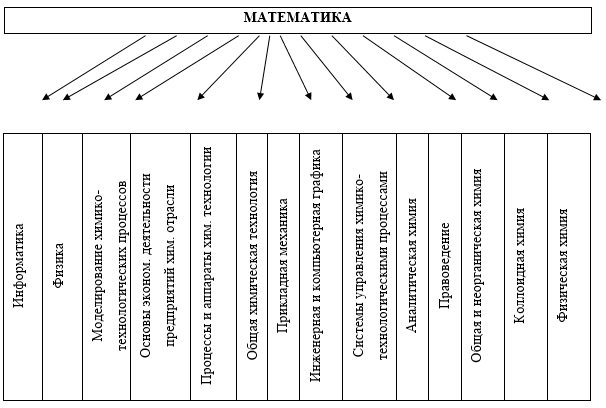
Учебные дисциплины, использующие математический аппарат
Сотрудничество с преподавателями выпускающих кафедр КНИТУ, участвующих в реализации профессиональных образовательных программ бакалавриата по направлению «Химическая технология», и результаты проведенного опроса позволили выявить наиболее востребованные в дисциплинах выпускающих кафедр элементы учебных разделов высшей математики (табл.) (востребованность оценивалась по пятибалльной шкале) [5].
Востребованность учебных разделов математики
Уровень востребованности |
Раздел математики |
Наиболее значимые понятия, навыки, темы |
Способ получения информации |
|
5 баллов |
Элементы высшей алгебры |
Понятия и методы алгебры матриц, определителей, различные методы решения систем линейных алгебраических уравнений |
Беседа, изучение литературы |
|
Элементы векторной алгебры |
Понятие вектора, операции над векторами, различные виды систем координат, понятие тензора, элементы тензорного исчисления |
||
|
Аналитическая геометрия на плоскости и в пространстве |
Прямая на плоскости, плоскость и прямая в пространстве и их взаимное расположение |
||
|
Дифференциальное исчисление функции одной переменной |
Понятия производной, дифференциала функции, его применение для приближенных вычислений, производные и дифференциалы высших порядков, производные от функции, заданной параметрически. Важно усвоить основные понятия об обыкновенных дифференциальных уравнениях первого и второго порядков, уметь решать системы линейных дифференциальных уравнений первого порядка, использовать элементы теории устойчивости |
||
|
Интегральное исчисление функции одной переменной |
Должны быть освоены понятия неопределенного и определенного интегралов, умение применять основные идеи и методы интегрирования |
||
|
Дифференциальное исчисление функции нескольких переменных |
Для функций двух и более переменных должны быть усвоены такие понятия, как «частные приращения», «частные производные», «полная производная», «полный дифференциал», «дифференцирование функции, заданной неявно», «частные производные» и «полные дифференциалы высших порядков». Важно знать понятия локального и условного экстремума функции двух переменных |
||
|
Кратные интегралы |
Умение вычислять двойной интеграл в декартовой и полярной системах координат |
||
|
Теория поля |
Характеристики скалярного и векторного полей: производная по направлению, градиент, дивергенция, ротор, циркуляция векторного поля, потенциальная функция, потенциальное поле |
||
|
Уравнения математической физики |
Важно уметь классифицировать дифференциальные уравнения II порядка с частными производными, знать и уметь применять методы их решения |
||
|
4 балла |
Аналитическая геометрия в пространстве |
Важно уметь строить поверхности II порядка: цилиндрические, конические поверхности, эллипсоиды, гиперболоиды, параболоиды |
Беседа, изучение литературы |
|
Функции одной переменной |
Понятия предела функции в точке и на бесконечности, бесконечно малых и бесконечно больших функций, понятия о неопределенностях и способах их раскрытия, первый и второй замечательные пределы, односторонние пределы, непрерывность функции, точки разрыва функции и их классификация |
||
|
Интегральное исчисление функции одной переменной |
Знать основные приложения определенного интеграла, понятия о несобственных интегралах |
||
|
Теория вероятностей |
Все основные формулы комбинаторики и классической теории вероятностей, понятия алгебры событий (вероятность суммы и произведения событий, формула полной вероятности, схема Бернулли). Случайные величины и их способы задания, числовые характеристики и различные законы распределения случайных величин, многомерные случайные величины |
||
|
Математическая статистика |
Уметь применять выборочный метод, уметь составлять и читать гистограммы и эмпирические функции распределения, уметь получать и вычислять характеристики выборки, точечные и интервальные оценки параметров распределения, составлять и проверять статистические гипотезы, знать элементы корреляционного анализа |
Анализ собранной информации показал, что в видении преподавателей выпускающих кафедр наиболее важными и наиболее востребованными элементами курса высшей математики для студентов, обучающихся по программам направления «Химическая технология», являются понятия и методы, относящиеся к таким разделам, как «Линейная алгебра», «Аналитическая геометрия», «Дифференциальное и интегральное исчисления», «Дифференциальные уравнения», «Теория поля», «Теория вероятностей» и «Математическая статистика».
Для набора студентов 2020 г. произошло существенное сокращение часов, выделенных на чтение лекций, при этом увеличилось количество часов, выделенных на самостоятельную работу. В подобных условиях мы предлагаем определить темы и задачи курса математики, наиболее значимые для понимания прикладных задач химической технологии, – такие темы и задачи, которые будут изучаться студентами совместно с преподавателем, и темы и задачи, которые можно вынести на самостоятельное изучение студентов (сопроводив необходимой методической литературой). Проведенная дифференциация материала курса позволяет более эффективно применять современные технологии обучения, в частности смешанную модель перевернутого обучения [6].
Содержание каждой изучаемой темы требует корректировки и дополнения абстрактных заданий по математике заданиями, имеющими профессиональную значимость. Остановимся на разделе «Линейная алгебра», который является безусловным лидером по востребованности для студентов, обучающихся по направлению 18.03.01 «Химическая технология».
Необходимость сокращения сроков разработки новых и усовершенствования действующих химических производств, их возрастающая сложность и разнообразие технологических процессов требуют принципиально нового подхода для математического описания задач, требующих вычисления скоростей реакций и расчета констант кинетических уравнений [7]. В кинетических уравнениях содержится информация об основных закономерностях протекания химических процессов. Она кладется в основу математической модели, описывающей химический процесс. Важно уметь проводить качественный и количественный анализ различных видов математических моделей, анализировать границы их применения к различным химическим процессам.
Рабочая программа по дисциплине «Математика» предлагает рассмотрение трех методов решения систем линейных алгебраических уравнений: метода Крамера, метода Гаусса и метода, использующего обратную матрицу. На наш взгляд, первый и последний методы можно предложить студентам для самостоятельного рассмотрения (вычисление определителей, действия над матрицами хорошо алгоритмизированы и не вызывают у обучающихся затруднений). Универсальный метод Гаусса более объемен по содержанию: основная и расширенная матрицы системы, ранг матрицы, определенность (неопределенность) системы, равносильность матриц, особенности применения, выбор ведущего элемента и иное требуют разбора на практических и лекционных занятиях совместно с преподавателем.
Приведем примеры заданий, использующих для решения метод Гаусса (абстрактный уровень и профессионально значимое задание).
Задание на абстрактном уровне.
I. Исследовать систему линейных уравнений:
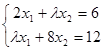 .
.
При каких значениях параметра 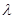 система: 1) несовместна; 2) совместна и не определена;
система: 1) несовместна; 2) совместна и не определена;
3) совместна?
Задание, имеющее профессиональную направленность.
II. Определить линейно независимые комбинации концентраций веществ, входящих в реакции:
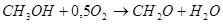
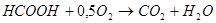
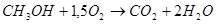
Подобным образом в курсе высшей математики для тем разделов, используемых для построения и анализа математических моделей химико-технологических процессов, абстрактные задания мы дополняем заданиями, имеющими профессиональную направленность. Подобранная таким образом база профессионально ориентированных задач позволит нам при решении проблемы подготовки специалиста, способного в будущем решать сложные мультидисциплинарные инженерные задачи.
Заключение
Проведенный анализ связей дисциплины «Математика» с дисциплинами основной образовательной программы, опрос преподавателей выпускающих кафедр позволили нам при проектировании содержания курса высшей математики обоснованно дифференцировать совокупность наиболее востребованных учебных элементов высшей математики для фундаментальной подготовки и для последующего успешного освоения профессионально ориентированных дисциплин.



