Заболевания позвоночника являются весьма распространенной патологией и постоянно требуют развития новых технологий для их лечения и возможного прогнозирования результатов хирургического пособия. Понимание биомеханических характеристик позвоночника служит ключевым элементом при разработке новых эффективных лечебных методик.
Позвоночно-двигательный сегмент позвоночника представляет собой сложную механическую систему, в которой диартродиальный дугоотросчатый сустав является важной анатомической структурой, обеспечивающей подвижность, восприятие вертикальных нагрузок и стабилизацию в каждом двигательном сегменте.
Анатомические, биомеханические и физиологические характеристики дугоотросчатых суставов позвоночника стали предметом повышенного внимания в связи с распространением хирургических вмешательств с установкой динамических и стабилизирующих имплантов, которые могут изменять биомеханические характеристики дугоотросчатых суставов.
Первые выводы о различных видах движений в позвоночно-двигательном сегменте позвоночника базировались на постановке сложных экспериментов на препаратах позвоночника [1]. Большое количество исследований было посвящено определению биомеханики позвоночника с использованием рентгенографических методов. Измерялись парные перемещения конечных точек при нормальных клинических движениях. Так, например, Knutsson et al. [2] обнаружил у некоторых пациентов аномальные трансляции позвонков в сагиттальной плоскости при сгибании и разгибании позвоночника. Установлено, что во время сгибания позвоночника передний сдвиг связан с дегенерацией диска [3]. Panjabi et al. [1] обсуждал проблемы надежности и точности, присущих рентгенографическому методу определения мгновенного центра вращения в любом суставе.
Механические свойства поясничных дугоотросчатых суставов были изучены Kingma et al. [4], который оценивал распределение нагрузки между диском и дугоотросчатыми суставами с помощью математической модели. Нагрузки на дугоотросчатые суставы определялись путем измерения деформации задних элементов позвонка [5]. Также были разработаны вычислительные модели, основанные на методе конечных элементов, которые позволяют проводить оценку напряженно-деформированного состояния позвоночно-двигательного сегмента и его тканей [6].
Несмотря на множество клинических и экспериментальных исследований биомеханики позвоночника в целом и кинематики в частности, данные о характере движений в позвоночно-двигательном сегменте в сагиттальной плоскости и о роли дугоотросчатых суставов в их осуществлении весьма разноречивы [7, 8]. Существующие варианты моделирования имеют ряд ограничений и не предназначены для воспроизведения перемещений суставных поверхностей друг относительно друга при осуществлении движений в позвоночно-двигательном сегменте.
Цель: определить влияние ориентации дугоотросчатых суставов позвоночника на кинематику движения в его сегментах в сагиттальной плоскости.
Материалы и методы исследования
Данное исследование было проведено в рамках комплексной научно-исследовательской работы Новосибирского НИИТО им. Я.Л. Цивьяна; протокол исследования был одобрен локальным этическим комитетом Новосибирского НИИТО, согласуется с требованиями Хельсинской декларации. В исследование были включены 48 пациентов амбулаторно-поликлинического отделения (возраст пациентов от 38 до 72 лет, средний возраст 53±15,6 года) без выраженной патологии позвоночника, не требующих хирургического лечения. Исходные данные определяли по рентгенограммам позвоночника в боковой проекции в положении стоя: отмечали координаты реперных точек с каждого позвонка в сагиттальной плоскости (рис. 1), необходимые для вычисления большого количества линейных и угловых величин, описывающих сложное строение позвонка [9, 10]. Наиболее значимые для данного исследования усредненные параметры представлены в таблице 1.
Таблица 1
Угол наклона суставных поверхностей позвонков
|
Позвонки |
Угол наклона суставной поверхности к вертикали, M ± m* |
|
|
Верхней |
Нижней |
|
|
С3-С7 |
27,7° ± 2,1° |
31,1° ± 3,0° |
|
Th1-Th12 |
21,6° ± 0,9° |
18,7° ± 0,6 |
|
L1-L2 |
7,1° ± 0,8 ° |
9,4° ± 1,6° |
|
L3-L5 |
–6,2° ± 1,4° |
9,4° ±° 1,6° |
|
S1 |
12,5°± 0,5° |
–** |
Примечание. * M – среднее значение, m – ошибка среднего, ** Знак (–) определяет отклонение плоскости суставной поверхности от вертикали по ходу часовой стрелки
Точкой сопоставления сочленяющихся пар суставных поверхностей позвонков определена середина суставных поверхностей. Таким способом воссоздавалось взаимоотношение смежных позвонков в каждом двигательном сегменте, определялась исходная высота межтелового промежутка – величина h.
Оригинальность разработанной нами математической модели [11] состоит в том, что сложное перемещение позвонка при сгибании и разгибании рассматривается как сложное движение, состоящее из двух последовательных простых движений (рис. 1).
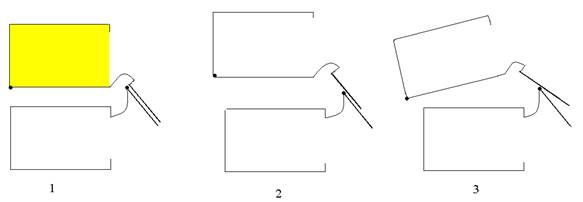
Рис. 1. Схема перемещения позвонка (1 – исходное положение; 2 – перемещение вышележащего позвонка в плоскости суставной поверхности верхних суставных отростков нижележащего позвонка; 3 – поворот вышележащего позвонка вокруг верхушки верхнего суставного отростка нижележащего позвонка)
Граничным условием для каждой фазы является перемещение точки каудо-вентрального угла тела позвонка по вертикали не более 0,5 высоты межтелового промежутка или длины суставной поверхности и не более 3,0 мм по горизонтали.
Математический аппарат модели
Рассчитываемые величины (рис. 2):
h – высота межтелового промежутка; α – угол поворота позвонка; Xc – линейное перемещение точки С1 по оси Ox; Zc – линейное перемещение точки С1 по оси Oz.
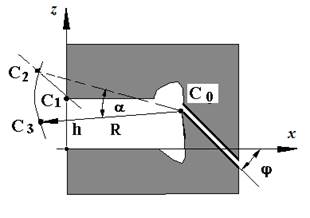
Рис. 2. Расчетная схема перемещения позвонка в сагиттальной плоскости
Кинематику движений в позвоночно-двигательном сегменте можно разделить на следующие этапы. В первой фазе перемещение точки C1 в новое положение C2 с координатами (x1, z1) происходит за счет параллельного смещения суставных поверхностей по суставной поверхности, точка C1 перемещается в положение точки C2. Отрезок C1C2 параллелен суставной поверхности и равен смещению по суставной поверхности. Во второй фазе происходит поворот вокруг точки C0 с координатами (x0, z0) по окружности радиусом R. Угол α характеризует поворот тела позвонка.
Исходными данными являются координаты (x0, z0), угол φ и положение точки C1(0, h), то есть исходная высота межтелового промежутка (величина h). По задаваемым координатам точки C3(x3, z3) необходимо найти угол α и длину отрезка |C1C2| = S.
При выполнении математических расчетов согласно геометрическим постулатам, которые детально изложены в предыдущих публикациях [9–11], были получены следующие выражения.
Величина смещения по суставной поверхности определяется как расстояние S между точками C1 и C2:
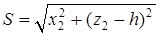 (1)
(1)
Угол поворота α определяется как угол между векторами |С0С3| и |С0С2|:
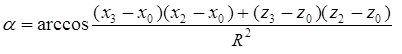 (2)
(2)
Граничное условие перемещения суставной поверхности в норме определено нами в пределах 0,5 ее длины, поскольку большее смещение расценивается как подвывих. Смещения тела позвонка по вертикали и по горизонтали задаются исследователем, тем самым моделируются амортизационная и удерживающая функции межпозвонкового диска.
С использованием данного математического аппарата была проведена серия экспериментов, которые заключались в изменениях параметров суставных поверхностей. Выполняется это следующим образом: вводятся исходные параметры ориентации и взаимного положения сочленующихся суставных поверхностей, а также допустимые значения горизонтального и вертикального перемещения вышележащего позвонка. Полученные величины угловых и линейных перемещений вышележащего позвонка в двигательном сегменте были оценены и интерпретированы.
Результаты исследования и их обсуждение
Результаты
Анализ выражения (2) позволяет заключить, что отсутствие линейных перемещений тела позвонка исключает его угловую дислокацию, что позволяет убедиться в правильности выбранного нами подхода. Как показали эксперименты, при нормальном положении суставных поверхностей перемещение тела позвонка на 2,0 мм по горизонтали и на 3,0 мм по вертикали дает максимальное значение угловых перемещений и составляет 16,0°. Допустимое изолированное смещение тела позвонка по вертикали до 3,0 мм включительно не создает патологической ситуации, и углообразование ограничивается 8,0°, что формирует дугу с величиной центрального угла в поясничном отделе 40,0°, а в грудном – 88,0° (табл. 2). На практике данная амплитуда в грудном отделе позвоночника не реализуется из-за жесткости каркаса грудной клетки. Для шейных позвонков аналогичное смещение тела позвонка создает ситуацию подвывиха позвонка на 0,5 длины суставной поверхности с величиной кифоза 9,7°. Добавление в этой ситуации смещения тела позвонка по вертикали (что моделирует разрыв фиброзного кольца, капсулы истинных суставов и связок позвоночника) приводит к нарастанию кифотической деформации.
Таблица 2
Угловое перемещение позвонка при вертикальных и горизонтальных смещениях
|
Позвонки |
По вертикали |
По горизонтали |
Результирующий угол |
|
С3-С7 |
3,0 |
2,0 |
16,0° |
|
3,0 |
– |
8,0° |
|
|
– |
6,0 |
15,5° |
|
|
Th1-Th12 |
3,0 |
– |
88,0° |
|
– |
1,0 |
9,5° |
|
|
L1-L5 |
3,0 |
– |
40,0° |
|
– |
1,0 |
9,5° |
Проведенные математические эксперименты по изменению значения угла наклона суставных поверхностей верхних суставных отростков нижележащего позвонка показали, что абсолютные значения возможных угловых перемещений позвонка и линейные перемещения между суставными поверхностями уменьшаются по мере приближения их к горизонтальной ориентации.
Отрицательное значение угла наклона суставной поверхности (отклонение суставной поверхности суставного отростка от вертикали по часовой стрелке), характерное для верхних суставных отростков L3, L4 и L5 позвонков (табл. 1), при изолированном снижении высоты диска вызывает эффект антелистеза. Потеря высоты диска в шейном и грудном отделах позвоночника создает эффект ретролистеза.
Задаваемое смещение тела позвонка только по горизонтали дает меньшее угловое перемещение между позвонками, чем смещение только по вертикали на ту же величину. Но при этом в первом случае смещение суставных поверхностей между собой больше, чем во втором. Данные результаты позволяют подтвердить положение о том, что при снижении удерживающей функции диска в сегменте создаются условия для возникновения подвывиха позвонка.
Анализ результатов при допускаемом равномерном смещении позвонка, как по вертикали, так и по горизонтали, при различных вариантах наклона суставных поверхностей позволяет прийти к заключению о том, что, чем более вертикально расположены суставные поверхности, тем при меньшей линейной дислокации суставных поверхностей достигается большее угловое перемещение позвонка.
Приближение суставных поверхностей к телу позвонка приводит к увеличению угла наклона позвонка при одинаковых величинах его линейных перемещений. Уменьшение длины суставных поверхностей приводит к более быстрому достижению граничных условий, соответствующих подвывиху позвонка, при меньших значениях угловых перемещений.
Задаваемое смещение тела позвонка только по горизонтали на 6,0 мм создает ситуацию верхового подвывиха позвонка с величиной кифоза 15,5°. Добавление в этой ситуации смещения позвонка по вертикали усиливает величину кифотической деформации до 30,0–40,0°.
Изолированное смещение тела позвонка по вертикали на всю высоту межпозвонкового диска (ситуация разрыва диска) приводит к образованию кифоза величиной 14,0°, при этом смещение суставных поверхностей происходит лишь на 2,5 мм, что нельзя назвать подвывихом по имеющимся классификациям.
Для грудных и поясничных сегментов, где ориентация суставных поверхностей более вертикальная, чем в шейном отделе позвоночника, допущение смещения по горизонтали даже на 1,0 мм создает картину подвывиха позвонка с величиной углового перемещения, равной 9,5° и более.
Обсуждение
Кинематика движений в позвоночно-двигательном сегменте, особенно в фокусе дугоотросчатых суставов позвонков, освещена недостаточно. Дугоотросчатый сустав имеет сложную анатомию, которая обеспечивает его уникальные функции сопротивления нагрузкам и обусловливает характер и амплитуду движения во всех отделах позвоночника. Форма и расположение суставных отростков оказывают наибольшее модифицирующее влияние на характер движений позвоночника в шейном и поясничном отделах позвоночника [1], [12]. Ориентация суставных поверхностей дугоотросчатых суставов различается на каждом уровне, особенно это заметно между отделами позвоночника. Суставные поверхности более ориентированы по горизонтали в шейном и верхнем грудном отделах позвоночника [13], что также подтверждается нашими данными. Эта анатомическая характеристика обеспечивает высокую степень сцепления осевого вращения и бокового изгиба в шейном отделе позвоночника [13]. В нижнегрудном и поясничном отделах позвоночника суставные поверхности становятся более вертикально ориентированными [14], что также ограничивает гибкость позвоночника как при боковом изгибе, так и при вращении в этих анатомических областях. Уменьшение амплитуды движений в позвоночно-двигательном сегменте защищает межпозвоночные диски и спинной мозг от нефизиологических кинематических и кинетических воздействий, которые могут привести к возникновению патологических состояний [15].
В результате создания нашей кинематической модели было подтверждено, что амплитуда линейного и углового перемещения позвонков друг относительно друга обусловлена ориентацией суставных поверхностей дугоотросчатых суставов. Вертикальная ориентация суставных поверхностей способствует большему угловому перемещению при минимальной линейной дислокации.
Было показано, что в норме во время движений поясничного отдела позвоночника в сагиттальной плоскости дугоотросчатые суставы вращаются вдоль медиолатеральной оси (в среднем на 2–6°) и перемещаются вертикально (в среднем на 2–4 мм) [16]. Моделирование такого изолированного вертикального смещения не приводит к клинически значимым дислокациям в грудном и поясничном отделах позвоночника. Однако в шейном отделе данное перемещение приводит к подвывиху – трансляция в сагиттальной плоскости даже на 2,0 мм может вызывать подвывих и кифотическую деформацию, несмотря на то, что нестабильностью считается трансляция позвонка более чем на 3,5 мм [1].
Предложенная нами модель основана на координатах точек суставных поверхностей дугоотросчатых суставов и точек вентральных отделов позвонков по данным рентгенограммы позвоночника в сагиттальной плоскости. Нами описано линейное и угловое перемещение точек при движении в дугоотросчатых суставах в норме и в случаях возможной нестабильности в позвоночно-двигательном сегменте; все перемещения ограничены анатомическими структурами.
Настоящее исследование имеет ряд ограничений. Данная математическая модель оценивает кинематику движения только в сагиттальной плоскости. Однако этот аспект находит большое применение в клинической работе, поскольку рентгенограммы, по которым выполняется маркировка координат, наиболее широко распространены в практике. Также детальное построение модели в сагиттальной плоскости позволяет расширить моделирование в трехмерном пространстве. Построение математической модели только с учетом положения структур позвонка, без оценки мышечно-связочного аппарата, то есть кинематической модели, является базой при моделировании позвоночника в целом, к тому же построение такой модели координат позвонков возможно на обычной рентгенограмме.
Предложенная модель может быть использована для описания других патологических состояний позвоночника (дегенеративных изменений, травм и пр.), а также при моделировании позвоночника, описании позвоночно-тазовых взаимоотношений. Этот стандартизированный подход наряду с методом конечных элементов станет использоваться в будущем для оценки существующих методик лечения и оптимизации имплантируемых конструкций.
Заключение
Амплитуда движений в дугоотросчатых суставах определяет движения во всем позвоночно-двигательном сегменте. Ориентация суставных поверхностей дугоотросчатых суставов ограничивает линейное и угловое перемещение позвонков друг относительно друга. Вертикальная ориентация суставных поверхностей обусловливает большее угловое перемещение при минимальной линейной дислокации. Наличие более коротких суставных поверхностей приводит к более быстрому достижению граничных условий, соответствующих подвывиху позвонка, при меньших значениях угловых перемещений.



