Мотивация является движущей силой в поведении и деятельности человека, она определяет эффективность любой деятельности субъекта, в том числе и образовательной. При осознанном выборе будущей профессии для студента характерна заинтересованность обучением, если же профессия была выбрана случайно, то наблюдается слабая мотивация к образовательному процессу. Но даже если студент учится на выбранной им специальности, не все учебные предметы кажутся ему необходимыми и важными для дальнейшей профессиональной деятельности. Такая проблема появляется, например, в обучении математике студентов гуманитарных направлений подготовки.
Цель исследования
Преподавателям математики в силу её абстрактности сложно заинтересовать студентов гуманитарных специальностей своим предметом, мотивировать необходимость его изучения, особенно если студент не имеет математических способностей. В этой ситуации преподаватель должен сделать акцент на то, что, несмотря на абстрактность математики в целом, её приложения активно применяются в различных областях, а математические модели являются моделями реальных процессов из окружающего мира. При этом невозможно знать математические приложения без знания основ математики.
Преподавателю по математике необходимо конструировать свой курс таким образом, чтобы:
- организовать образовательную деятельность для студентов с максимальным использованием особенностей и возможностей своего предмета;
- на примере решения профессионально ориентированных задач давать возможность студентам увидеть необходимость математики в профессиональной деятельности;
- рационально подходить к планированию и осуществлению самостоятельной работы;
- обеспечивать формирование общих умений и навыков самообразования.
Обобщённой целью исследования является разработка примеров прикладных задач математики, для студентов специальности 38.05.02 Таможенное дело, позволяющих мотивировать студентов к изучению дисциплины и формирующих их личную заинтересованность в получении знаний.
Материалы и методы исследования
Примером обучения математике с использованием профессионального ориентирования может служить следующий вариант. Специалистам таможенного дела необходимо обладать знаниями, находящимися в двух областях – юриспруденции и экономики. Уникальность характеризуемой специальности ставит новые цели и задачи перед математикой. Управление процессами в области таможенного дела, выявление тенденций их развития, интерпретация информации по юридическим и экономическим вопросам, её хранение, сбор, анализ и оценка статистических данных – это те проблемы, которые возникают на стыке математики и таможенного дела.
Дисциплина «Математика» должна обеспечивать формирование следующей компетенции: способность использовать основы экономических и математических знаний при оценке эффективности результатов деятельности в различных сферах (ОК–7) [1]. Дисциплинами, при изучении которых также формируется эта компетенция, являются: «Экономическая теория», «Ценообразование во внешней торговле», «Системный анализ в таможенном деле». Поэтому студенты таможенного дела при изучении математики должны иметь представление о применении математики в экономике и социально-экономических исследованиях.
Приведём примеры профессионально ориентированных задач, которые помогают студентам таможенного дела увидеть возможности применения математики в экономике.
Результаты исследования и их обсуждение
В разделе «Линейная алгебра с элементами аналитической геометрии» можно отметить возможности применения действий с матрицами при однообразных математических операциях с массивами чисел. Примером может послужить следующая задача.
Пример 1. Рассчитайте размер таможенной пошлины (в валюте РФ) на ввозимый на территорию РФ товар. Партия товара представляет собой продукцию трёх видов: А, В, С. Известно, что таможенная стоимость продукции вида А равна 3500 рублей, для вида В стоимость составляет 4500 рублей, для С – 2000 рублей. Ставка пошлины для каждого вида продукции соответственно равна 25, 30 и 20% [2, c. 68].
Стандартным решением этого примера станет нахождение 25% от числа 3500, 30% от 4500 и 20% от 2000, т.е. проведение следующих действий: 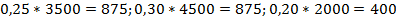 . Сумма полученных результатов даёт итоговый ответ 2625 рублей.
. Сумма полученных результатов даёт итоговый ответ 2625 рублей.
В процессе такого решения производятся однообразные действия нахождения процентов, однако с помощью матриц такая задача решается в одно действие.
Представим партию товара, состоящую из трёх видов матрицей 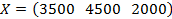 , а ставки пошлины для каждого из товаров – матрицей
, а ставки пошлины для каждого из товаров – матрицей 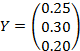 . Тогда искомый размер таможенной пошлины на весь товар
. Тогда искомый размер таможенной пошлины на весь товар 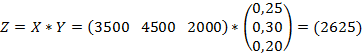 .
.
Далее можно привести пример более сложной задачи, которая показывает возможности матричной алгебры. Например, требуется определить общую стоимость сырья на каком-нибудь предприятии при условии, что используют несколько видов сырья для нескольких типов продукции, причём известно количество единиц продукции и стоимость каждого вида сырья. Эта задача является моделью реальной задачи в области экономики и если подобную задачу решать без использования матриц, то необходимо также осуществлять однообразные арифметические операции, что может занять продолжительное время.
В разделе «Введение в математический анализ» студенты специальности «Таможенное дело» должны ознакомиться с различными функциональными зависимостями, встречающимися в таможенной практике. Примерами таких зависимостей являются зависимости спроса и предложения от цены, зависимость объёма выпускаемой продукции от объёма перерабатываемого ресурса, зависимость налоговой ставки в процентах от величины годового дохода и т.д.
Для экономики представляет интерес условие равновесия – это равенство спроса и предложения, что задаётся формулой D(S) = S(P) и соответствует точке М (точка равновесия) пересечения кривых спроса D и S. Приведём пример задачи на экономический эффект по разделу «Введение в математический анализ».
Пример 2. На графике (рисунок) изображены кривые спроса (D) и предложения (S) в небольшой стране. Оси абсцисс и ординат выражают соответственно объём в штуках и цену в евро. Также на графике изображена линия мировой цены (Т). Определите, является ли эта страна импортером или экспортером, и поясните свой ответ.
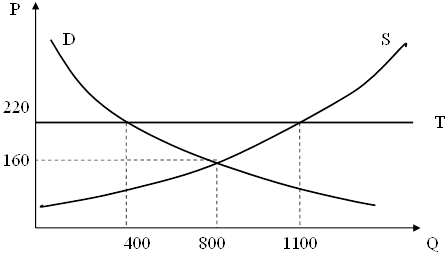
Условие к задаче на экономический эффект
Решение задачи следующее. В отсутствие торговли страна производит и потребляет продукцию в объёме 800 штук по цене 160 евро. Возможность продажи продукции по более высокой цене другой стране будет побуждать производителей стремиться увеличивать производство. При цене 220 евро небольшая страна сможет увеличить производство продукции до 1100 штук, его предложение (кривая предложения S), будет выше установившегося до начала торговли национального спроса (линия спроса D). Потребление продукции в малой стране при цене в 220 евро составит 400 штук. Излишек предложения над спросом 1100 – 400=700 будет экспортироваться за границу. Ответом будет следующее: небольшая страна является экспортёром.
При разборе такой задачи формируются навыки работы с графиками: распознавание основных элементарных функций, умение находить значения функций, изображённых графически, но при этом также формируются межпредметные связи с экономикой, поскольку при решении задачи необходимо владеть знаниями из этой дисциплины.
В числе упражнений, относящихся к этому разделу, следует указать задания на использование пределов в социально-экономической сфере.
Пример 3. Дана зависимость спроса Р от цены Q:
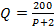 . Изучить поведение функции спроса при неограниченном увеличении цены
. Изучить поведение функции спроса при неограниченном увеличении цены 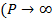 ).
).
Решение заключается в нахождении предела 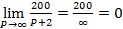 . Таким образом, при бесконечном росте цены спрос приближается к нулю.
. Таким образом, при бесконечном росте цены спрос приближается к нулю.
В школьном курсе математики не показывается экономический смысл производных, однако студентам специальности «Таможенное дело» необходимо освоить раздел дифференциального исчисления с позиции применения производных в экономике, поскольку этот материал пригодится им при изучении последующих дисциплин курса.
Дифференциальное исчисление функций одной переменной применяется при исследовании эластичности спроса и предложения, для определения максимальных чистых выгод, для анализа потребительского поведения, при расчёте максимальной прибыли. Следующий пример включает в себя достаточно большое количество математических операций с производными, активно применяемых в экономике.
Пример 4. Предприятие выпускает и реализует продукцию в объёме Q, усл. ед. известны функции затрат 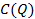 и цены продукции P(Q):
и цены продукции P(Q): 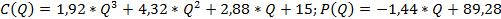 .
.
Требуется определить:
1) максимальную прибыль предприятия;
2) объём продукции и цену, соответствующие максимальной прибыли;
3) средние и предельные затраты, соответствующие максимальной прибыли;
4) участки роста и убывания прибыли при изменении объёма выпускаемой продукции от 2 до 5 усл. ед.;
5) наименьшее значение затрат при изменении объёма выпускаемой продукции от 2 до 5 усл. ед. [3, c. 68].
В данной задаче рассматривается нахождение:
– функции дохода 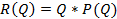 ;
;
– прибыли от реализации произведённой продукции 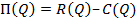 ;
;
– объёма продукции, при котором прибыль максимальна, то есть значения Q , удовлетворяющего уравнению 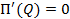 ;
;
– максимального значения прибыли при найденном значении объёма продукции;
– средних издержек на единицу продукции 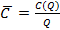 ;
;
– предельных издержек, то есть первой производной от функции затрат на производство продукции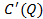 ;
;
– наименьшего значения затрат из условия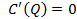 .
.
Функции нескольких переменных позволяют расширить спектр использования указанных ранее функций, связав их с несколькими видами продукции. Одним из вариантов задач по данной теме может служить задача на нахождение экстремума функции двух переменных.
Пример 5. На фабрике производятся товары двух видов в количествах соответственно x и y. Цены на эти товары, соответственно, составляют P1=32 и P2=24 денежные единицы. Найти количество обоих видов товаров, которое необходимо произвести, чтобы получить наибольшее значение прибыли, если функция издержек имеет вид 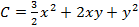 .
.
В разделе «Дифференциальное исчисление функций одной переменной» студенты были ознакомлены с функцией прибыли П(Q) и рассматривали задачи на нахождение максимальной прибыли для одного вида товаров, то есть решали уравнение 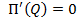 . В данной задаче для нахождения максимального значения прибыли необходимо решить систему линейных уравнений
. В данной задаче для нахождения максимального значения прибыли необходимо решить систему линейных уравнений  после чего проверяется, определяет ли найденная точка локальный экстремум функции прибыли.
после чего проверяется, определяет ли найденная точка локальный экстремум функции прибыли.
В разделе «Интегральное исчисление» также прослеживается связь с профессией, поскольку для решения задач необходимо знание специальных экономических понятий: понимание экономического смысла математических характеристик кривой Лоренца, смысла коэффициента Джинни. Одной из задач на использование интегрального исчисления в экономике может быть следующая задача.
Пример 6. По данным исследований в распределении доходов одной из стран, кривая Лоренца может быть описана уравнением 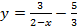 , где x – доля населения, y – доля доходов населения. Вычислить коэффициент Джинни, оценить распределение доходов 40% наиболее низко оплачиваемого населения [3, c. 69].
, где x – доля населения, y – доля доходов населения. Вычислить коэффициент Джинни, оценить распределение доходов 40% наиболее низко оплачиваемого населения [3, c. 69].
Решением будет нахождение определённого интеграла 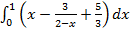 и вычисление коэффициента Джинни.
и вычисление коэффициента Джинни.
Многочисленные приложения во многих областях, в том числе и в экономике, имеют дифференциальные уравнения. Студентам таможенного дела необходимо знать, что анализ закономерностей процессов, происходящих в обществе, приводит к рассмотрению математических моделей, основой которых являются дифференциальные уравнения. Например, дифференциальное уравнение с разделяющимися переменными вида 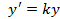 , имеющее решение
, имеющее решение 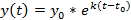 , где
, где  , описывает рост народонаселения, динамику роста цен при постоянной инфляции и имеет другие применения в экономике, при этом следует отметить, что данное дифференциальное уравнение применительно и к другим областям знаний, например, оно описывает процесс радиоактивного распада. Приведём пример использования дифференциальных уравнений в экономике.
, описывает рост народонаселения, динамику роста цен при постоянной инфляции и имеет другие применения в экономике, при этом следует отметить, что данное дифференциальное уравнение применительно и к другим областям знаний, например, оно описывает процесс радиоактивного распада. Приведём пример использования дифференциальных уравнений в экономике.
Пример 7. Функции спроса D=D(t) и предложения S=S(t) от цены товара P, где t –время, имеют следующие аналитические выражения: 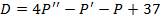 и
и 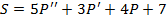 . Найти зависимость цены P=P(t) от времени t при равновесном состоянии рынка [4, c. 21].
. Найти зависимость цены P=P(t) от времени t при равновесном состоянии рынка [4, c. 21].
Для определения равновесной цены следует решить уравнение 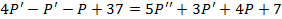 , которое после упрощения примет вид:
, которое после упрощения примет вид: 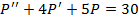 . Данное дифференциальное уравнение относится к классу неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
. Данное дифференциальное уравнение относится к классу неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Студентам таможенного дела необходимо знать, что аппарат теории вероятностей активно используется в экономике при анализе стохастической модели рынка, а также для вероятностных расчетов в текущем анализе хозяйственной деятельности, прогнозирования и построения рационального поведения социально-экономических систем. Приведём пример профессионально ориентированной задачи по повторным испытаниям.
Пример 8. Вероятность правильного оформления декларации на товары (ДТ), оформляемой при перевозке груза через границу равна 0,8. Найти вероятность того, что из трёх ДТ только две оформлены правильно [5, с. 35].
По сравнению с предыдущими разделами дисциплины «Математика», раздел «Элементы теории вероятностей и математической статистики» студентами таможенного дела осваивается гораздо легче. Это обусловлено психологические особенности мышления «гуманитариев». У таких обучающихся преобладает наглядно-образное мышление, богатое воображение, ярко выраженная эмоциональность восприятия окружающей действительности, значительный интерес к занимательному материалу. Теория вероятностей даёт возможность приводить разнообразные интересные примеры. Рассмотрим пример занимательной задачи из темы «Элементы комбинаторики».
Пример 9. В среду у группы ТД-71 в расписании 3 пары. Всего группой в семестре изучается 10 различных дисциплин. Сколькими способами можно составить расписание на среду так, чтобы дисциплины не повторялись.
В подобной задаче можно изменять название группы, день недели и количество дисциплин в соответствии с группой, у которой проводится занятие. Это поддерживает интерес к предмету, поскольку у студентов присутствует личная заинтересованность в задаче.
Выводы
Представленные варианты межпредметной связи математики и экономики позволяют получить грамотного специалиста в области таможенного дела. Следует отметить важность исследовательской работы в поиске новых методов подачи материала: выяснения наиболее эффективной последовательности изложения тем, дополнение примерами, относящимися к конкретной профессии, которые помогут студенту в дальнейшей работе.



