На современном этапе развития образования результаты усвоения физических знаний школьниками оцениваются в ходе проведения итоговой государственной аттестации, которая в зависимости от возраста и выбора обучающегося может иметь формат Основного государственного экзамена (ОГЭ), Единого государственного экзамена (ЕГЭ) или Всероссийской проверочной работы (ВПР) по физике.
Анализ контрольно-измерительных материалов, предлагаемых школьникам, показывает, что в большинстве случаев их знания оцениваются по сформированности умения применять физические понятия и законы в процессе решения физических задач [3, 4, 9]. Мы считаем, что школьник будет готов к любому виду итоговых испытаний по физике, если в процессе обучения будет организована деятельность обучающихся, направленная на овладение методами решения физических задач. Анализ физических задач-проблем позволяет констатировать, что они могут быть решены с опорой на обобщенный метод [10]. Чтобы обучение обобщенному методу было эффективным, при изучении конкретных разделов физики необходимо организовать деятельность школьников по усвоению частных методов решения физических задач. Основными среди них являются:
1) координатный метод;
2) динамический метод;
3) метод решения задач по теме «Статика»;
4) энергетический метод;
5) термодинамический метод;
6) метод решения задач по теме «Основы молекулярно-кинетической теории»;
7) метод построения изображений в оптических системах;
8) метод равных потенциалов.
Практика обучения решению задач, сложившаяся в школе, состоит в том, что ученики решают различные задачи либо методом проб и ошибок, либо по образцу, который показывает учитель или ученик, вызванный к доске. Такой способ обучения нельзя считать эффективным, потому что, во-первых, физических задач огромное множество и перерешать все их невозможно в силу ограниченности временного ресурса. Во-вторых, процесс решения задачи каждым учеником неуправляем со стороны учителя и во многом зависит от личностных качеств обучающегося. В-третьих, ученики не могут абстрагироваться от несущественных для решения конкретных задач признаков и перенести навык при решении других задач.
Для успешной подготовки учеников к любым видам контроля по физике необходимо, чтобы каждый из них овладел всеми методами решения физических задач. Эффективность освоения метода в целом напрямую зависит от сформированности у школьников действий, входящих в содержание метода. Поэтому при изучении каждой темы школьного курса физики, необходимо на уроке организовать этап применения знаний. Методика организации деятельности школьников, направленная на усвоение физических знаний, описана в работах [6, 7, 8]: в работе [7] описан способ организации познавательной деятельности школьников по усвоению знаний, необходимых для формирования термодинамического метода; в работе [8] – метода построения изображений в оптических системах.
Опишем методику организации деятельности школьников, направленную на усвоение метода решения физических задач. Реализация этой методики требует от учителя физики специальной подготовительной работы, а именно, необходимо:
1. Подобрать 10–13 задач, разного уровня сложности.
2. В процессе решения выделить обобщенные действия, выполнение которых приводит к достижению цели поставленной задачи, и составить метод решения.
3. Разработать дидактические средства, включающие в себя раздаточный материал для организации деятельности учеников на уроке и контроля их знаний.
4. Подготовить презентацию, включающую в себя опорные знания, необходимые для выполнения действий метода; систему задач, решение которых позволяет сформировать метод у школьников; содержание формируемого метода в виде последовательности действий; решение конкретных задач с опорой на обобщенный метод.
Опишем методику организации деятельности школьников по усвоению координатного метода решения физических задач.
В конце изучения раздела «Кинематика» или «Механические явления» необходимо спланировать 3 урока физики – два из них на формирование метода у школьников, третий урок – на контроль усвоения метода.
Урок следует начинать с актуализации опорных знаний, проводимой в форме фронтального опроса. В результате этого этапа у учеников в тетради и на слайде презентации систематизируются необходимые физические понятия и законы в виде опорного конспекта. На рисунке 1 приведен вид слайда, на котором описаны физические законы, характеризующие равномерное и равноускоренное движения. Также учащиеся вспоминают, как правильно выбрать систему отсчета (рис. 2).

Рис.1. Опорные знания физических законов
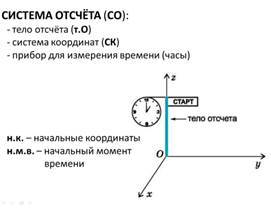
Рис.2. Опорные знания по системе отсчета
После актуализации опорных знаний учащимся предъявляются семь задач, при решении которых будет использоваться изучаемый метод решения физических задач – координатный. Для этого задачи демонстрируются на слайде и раздаются учащимся в печатном виде.
Приведем возможные формулировки задач, решение которых позволяет сформировать у школьников координатный метод.
1. С высоты h над Землёй падает тело. С Земли из точки, находящейся на расстоянии l по горизонтали от линии падения тела, производится выстрел из винтовки так, что пуля вылетает под углом к горизонту со скоростью ![]() . Под каким углом должна располагаться винтовка, чтобы пуля попала в тело, если выстрел производится одновременно с началом падения [2]?
. Под каким углом должна располагаться винтовка, чтобы пуля попала в тело, если выстрел производится одновременно с началом падения [2]?
2. С какой высоты h упало тело, если последний метр своего пути оно прошло за время t1 = 0,1 с[2]?
3. С вертолёта, поднимающегося вертикально вверх со скоростью ![]() , с высоты h над Землёй отпускают тело. Определить через сколько времени оно упадёт на Землю и с какой скоростью [2].
, с высоты h над Землёй отпускают тело. Определить через сколько времени оно упадёт на Землю и с какой скоростью [2].
4. Какую минимальную скорость должен иметь мотоциклист при отрыве от края трамплина с углом наклона к горизонту α, чтобы перепрыгнуть ров шириной S, если высота края трамплина h [2]?
5. Камень брошен на склоне горы под углом α к её поверхности. Определить дальность полёта камня, если начальная скорость камня равна ![]() , угол наклона горы к горизонту β. Сопротивление воздуха не учитывать [1].
, угол наклона горы к горизонту β. Сопротивление воздуха не учитывать [1].
6. Волчок, имеющий форму конуса высотой h и радиусом основания r, быстро вращается вокруг своей оси и движется поступательно по ровной поверхности стола со скоростью υ. В какой-то момент времени волчок соскакивает со стола. При какой скорости υ при падении волчок не заденет край стола [5]?
7. Утка летела по горизонтальной прямой с постоянной скоростью ![]() . В неё бросил камень неопытный охотник, причём бросок был сделан без упреждения, т.е. в момент броска скорость камня
. В неё бросил камень неопытный охотник, причём бросок был сделан без упреждения, т.е. в момент броска скорость камня ![]() была направлена как раз на утку под углом α к горизонту. На какой высоте летела утка, если камень всё же попал в неё? Сопротивлением воздуха, размерами утки и ростом охотника пренебречь [11].
была направлена как раз на утку под углом α к горизонту. На какой высоте летела утка, если камень всё же попал в неё? Сопротивлением воздуха, размерами утки и ростом охотника пренебречь [11].
Первую задачу учитель разбирает с учащимися, поэтапно выявляя потребность в выполнении конкретных действий и реализуя их. В результате на доске и в тетрадях у учащихся возникает решение первой задачи с выделенными этапами решения.
Далее учащимся предлагается проанализировать этапы решения задачи и выявить последовательность действий, приводящую к достижению цели. Учитель организует деятельность учащихся на обсуждение полученных результатов, и на экран последовательно выводятся действия, составляющие содержание координатного метода решения физических задач, которые ученики записывают в тетрадях.
1. Изобразить графическую модель, указав на ней движущиеся тела, траектории их движения, векторы скоростей и ускорений.
2. Определить характер движения тел и записать векторные уравнения, описывающие данный вид движения.
3. Выбрать систему отсчёта.
4. Записать в скалярном виде законы движения тел.
5. Определить параметры движения тела (x0, y0, υ0x, υ0y, ax, ay) в начальный момент времени (начальные параметры движения).
6. Записать законы движения тел, с учетом начальных параметров движения.
7. Выбрать другой момент времени и определить координаты тел в этот момент времени.
8. Записать уравнения движения тел в другой момент времени.
9. Решить полученную систему уравнений относительно искомой физической величины.
Вторую задачу учащимся предлагается решить самостоятельно в тетрадях, проговаривая и обсуждая результат выполнения каждого действия метода. Учащиеся поочередно выходят к доске и последовательно реализуют этапы решения задачи.
Следующие две задачи учащимся предлагается решить по вариантам: один вариант решает задачу № 3, другой вариант – задачу № 4. Через 10 минут учащиеся меняются задачами – один вариант решает задачу № 4, другой – задачу № 3. Решение обсуждается с учащимися, на слайдах, с настроенной по щелчку компьютерной мыши анимацией, демонстрируется действие метода и результат его реализации при решении данных задач.
Далее учащиеся решают последовательно задачи 5, 6 и 7. Задачи, которые не разбирались в классе, предлагаются учащимся в качестве домашнего задания.
Приведем пример поэтапного решения задачи № 6 координатным методом.
1. Изобразить графическую модель, указав на ней движущиеся тела, траектории движения, векторы скоростей и ускорений.
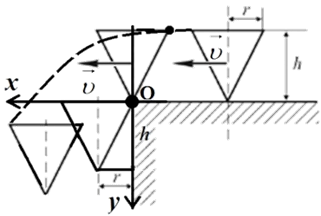
Рис.3. Графическая модель задачи № 6
2. Определить характер движения тел и записать векторные уравнения, описывающие данный вид движения.
Равноускоренное движение: ![]() ;
;![]() .
.
3. Выбрать систему отсчёта (СО): тело отсчета – Земля; система координат – прямоугольная декартовая; OX – горизонтально влево; OY – вертикально вниз; начало координат – в точке О на углу стола; начальный момент времени – момент соскока волчка.
4. Записать в скалярном виде законы движения тел.
![]() ;
; ![]() ;
;
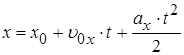 ;
; 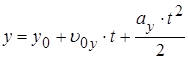 .
.
5. Определить параметры движения тела (x0, y0, υ0x, υ0y, ax, ay) в начальный момент времени (начальные параметры движения).
При t = 0 – момент соскока: ![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
; ![]() .
.
6. Записать законы движения тел, с учетом начальных параметров движения.
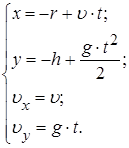
7. Выбрать другой момент времени и определить координаты тел в этот момент времени.
При t – момент времени, когда при падении волчок касается края стола:
![]() ;
; ![]() .
.
8. Записать уравнения движения тел в данный момент времени.
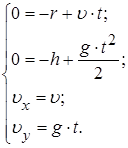
9. Решить полученную систему уравнений относительно искомой физической величины.
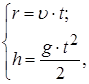
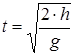 ;
;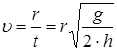 .
.
Таким образом, волчок не заденет край стола, если при падении будет иметь горизонтально направленную скорость 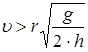 .
.
На контрольном этапе учащимся предлагается по вариантам решить несколько задач. Их следует располагать в порядке усложнения. Приведем примеры задач для контроля усвоения учениками координатного метода:
1. Два автомобиля движутся навстречу друг другу с постоянными скоростями υ1 и υ2. Первый автомобиль проходит пункт A на промежуток времени Δt раньше, чем второй проходит пункт B. Определить когда и где произойдет их встреча, если расстояние между A и B равно s [2].
2. Два тела бросили одновременно из одной точки: одно вертикально вверх, другое – под углом α = 60° к горизонту. Начальная скорость каждого тела υ0 = 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через t = 1,7 с [4].
3. Артиллерийское орудие расположено на горе высотой h. Снаряд вылетает из ствола со скоростью ![]() , направленной под углом α к горизонту. Пренебрегая сопротивлением воздуха, определите скорость снаряда в момент падения [1].
, направленной под углом α к горизонту. Пренебрегая сопротивлением воздуха, определите скорость снаряда в момент падения [1].
4. Два автомобиля движутся прямолинейно в одну сторону с постоянными скоростями υ1 и υ2 (причем υ1>υ2), и в некоторый момент времени расстояние между ними равно s. Через сколько времени и в каком месте первый автомобиль догонит второй [2]?
5. Тело брошено вертикально вверх с начальной скоростью υ0 = 3,13 м/с. Когда оно достигло верхней точки полета, из того же начального пункта с такой же начальной скоростью бросили второе тело. Определите, на каком расстоянии h от точки бросания встретятся тела. Сопротивление воздуха не учитывать [1].
6. Артиллерийское орудие расположено на горе высотой h. Снаряд вылетает из ствола со скоростью ![]() , направленной под углом α к горизонту. Пренебрегая сопротивлением воздуха, определите дальность полёта снаряда по горизонтальному направлению [1].
, направленной под углом α к горизонту. Пренебрегая сопротивлением воздуха, определите дальность полёта снаряда по горизонтальному направлению [1].
Реализация всех этапов методики позволяет каждому ученику усвоить координатный метод и научиться применять его для решения задач в любых конкретных ситуациях при прохождении любых итоговых испытаний по физике. Применение в процессе организации деятельности школьников презентации или интерактивной доски делает процесс усвоения метода более эффективным, позволяет разбирать непонятные учащимся моменты, помогает наглядно демонстрировать ход решения физических задач.



