Анализ исследований, посвященных методике обучения математике в высшей школе, позволяет утверждать, что эта научная проблема является предметом активных поисков в области дидактики и методики. Инновационными во многих отношениях являются принципы профессиональной направленности, построения системы междисциплинарных связей, обладающих многомерностью и сложной структурой [1].
Применение проблемного обучения в учебном процессе рассматривается в работах В. Медведева, Н. Поляковой, В. Дрибана, А. Ровенской, В. Кушнира и других. Формированию исследовательских умений в процессе обучения посвящены работы А. Тимошенко, Г. Ельчанинова, Н. Анисимова и др. Концепцию многоуровневой математической подготовки на базе интегрированных форм занятий и контроля сформулировали Т. Устюжанин, А. Гафиятова, Н. Полякова и др. Вопросу реализации контекстного обучения в процессе преподавания математики уделяется внимание в исследованиях А. Вербицкого, Н. Никитиной и др. [6].
Изложение основного материала. Говоря об инновационных методах обучения математике, В. Кушнир настаивает на том, что система обучения, построенная на инновационных принципах, является синергетической системой, то есть предполагает нарушение устойчивости учебного процесса с целью возникновения его новых диссипативных (более открытых для нововведений) структур [3]. В. Дрибан отмечает, что преподавание математики должно способствовать формированию научного мировоззрения, развитию творческого мышления [7]. Этот же вопрос развивает А. Тимошенко, изучая проблему формирования в процессе обучения высшей математике исследовательских умений [2]. Эффективность применения проблемных ситуаций при изучении математических дисциплин исследуется и другими авторами [4].
Одним из главных методов профессиональной подготовки специалистов технических специальностей, формирующим принцип профессиональной направленности, является проблемное обучение. При применении проблемного обучения математические понятия, закономерности и теории изучаются в ходе поиска, наблюдения и анализа, что позволяет студентам применить их к изучению специальных дисциплин [5].
На производительности проблемного подхода в преподавании высшей математики для инженерных специальностей настаивает А. Ровенская, которая отмечая отсутствие у студентов технических вузов должного представления об использовании математических знаний и умений в будущей профессиональной деятельности, утверждает, что познавательный интерес к изучению математики развивается с помощью методологии обязательств проблемных ситуаций, способствующих формированию заинтересованности по овладению будущей профессии инженера у студентов инженерных специальностей [8].
С целью повышения эффективности обучения математике проблемный метод рекомендуется сочетать с другими, чтобы избежать односторонности. Стоит заметить также, что проблемное выяснения всех вопросов учебного материала нецелесообразно в дидактическом аспекте. Оптимальным видится комплексное сочетание других методов обучения с проблемным.
Не менее эффективной инновационной методикой, как и проблемное обучение, является опора на принцип профессиональной направленности, контекстное обучение.
Цель реализации контекстных технологий заключается в стремлении преподавателя преодолеть противоречия:
- между формами учебной деятельности студентов в вузах и формами будущей профессиональной деятельности выпускников;
- между пассивной ролью студента в учебе и инициативной позицией специалиста к трудовой деятельности.
Содержательную основу технологий контекстного обучения составляют следующие типы проблемных (квазипрофессиональных) ситуаций:
- интеллектуальные ситуации (содержат сведения когнитивного характера будущей профессиональной деятельности, в частности о сущности функциональных обязанностей специалиста, о требованиях к профессионально важным качествам и компетенциям специалиста и т.д., а также предполагают самоанализ студентом своей профессиональной подготовленности к трудовой деятельности);
- эмоционально-личностные ситуации (способствуют формированию позитивного отношения к будущей профессии, осознанию проблем адаптации к реальным условиям труда);
- регулятивно-поведенческие ситуации (предусматривают выбор модели поведения в конкретных деловых ситуациях, способствуют повышению адаптивных возможностей студентов).
Реализация в учебном процессе современного высшего учебного заведения технологий контекстного обучения, разработанная А. Вербицким, предполагает, что знания усваиваются студентами в контексте решения моделируемых учебно-профессиональных ситуаций; обусловливает развитие профессиональной мотивации и профессионального мышления будущего специалиста, личностных смыслов процесса обучения.
Система применения педагогической инноватики в математической подготовке студентов инженерно-технических специальностей должна строиться на основе поэтапного подхода. На основе анализа педагогической литературы мы формулируем основные этапы изучения математики:
- определение и осознание новых понятий, их взаимосвязь с жизненным опытом и полученными ранее знаниями;
- простейшие задачи, которые ставят целью лучше понять определения, их связи между собой и тем, что усвоено ранее, мотивация введения этих понятий и определений;
- тренинг и развитие, что позволяет овладеть навыками, усовершенствовать умения, научиться быстро работать с новым материалом, который был осознанным и мотивированным на первом этапе;
- творчество и исследовательская деятельность, что позволяет достичь глубин нового знания, на принципиально ином уровне увидеть его взаимосвязь с явлениями иного порядка, сформулировать вопросы и задачи.
Вышеупомянутая профессионально направленная многоуровневая математическая подготовка студентов технических специальностей может быть представлена в виде следующей схемы (рисунок).
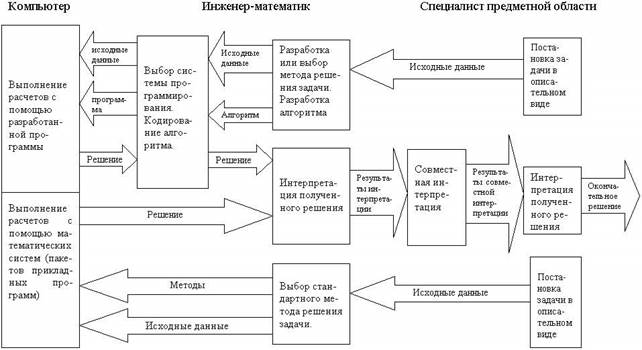
Модель многоуровневой математической подготовки с применением приемов педагогической инноватики
Определение критериев – одна из сложнейших задач педагогической науки. В психолого-педагогических исследованиях для количественной оценки сформированности или развития качеств, умений, навыков, компетенций, направленности подготовленности обосновывается целесообразность использования различных критериев. Критерий (от греч. Kriterion - средство для суждения) – признак, на основе которого осуществляется оценка, определение или классификация; мерило оценки. В справочной и специальной литературе критерий определяется как средство для суждения, признак, на основании которого осуществляется определение или классификация чего-либо, мерило оценки. Вопрос критериев связан с мерами повышения эффективности профессиональной деятельности. Это вопрос о том, какие параметры данного процесса необходимо измерять.
В своей работе мы исходим из следующего определения: критерий – это признак, на основании которого проводится оценка; средство проверки, мерило оценки. Другими словами – это совокупность отличительных признаков, позволяющих осуществить оценку сформированности профессиональной направленности студентов инженерного профиля.
В нашем исследовании мы выделяем следующие критерии оценки профессиональной направленности:
- мотивационный;
- когнитивный;
- технологический.
Мотивационный критерий означает уровень сформированности профессиональной направленности личности будущего инженера. Показателями мотивационного критерия выступают: осознание важности профессии инженера, социальная ответственность; мотивация достижения успеха и интерес в профессиональной деятельности.
Когнитивный критерий – уровень усвоения будущим специалистом приобретенных профессиональных знаний. Показателями когнитивного критерия выступают: овладение профессионально значимыми знаниями (фундаментальными, специальными, психолого-педагогическими, управленческими, научно-методическими, предметными, технологическими, проектировочными).
Технологический критерий – уровень овладения умениями и навыками, необходимыми для профессиональной деятельности будущего инженера. Показателями технологического критерия являются: овладение будущими специалистами - инженерами умениями работы с информацией, ориентация на самосовершенствование в радиотехническом проектировании через графическую визуализацию замысла.
Разработанные тестовые вопросы и варианты ответов позволили авторам выявить три уровня сформированности профессиональной направленности будущего радиста: высокий, средний и низкий.
Для низкого уровня характерны: несформированность компонентов профессиональной направленности, не проявляется интегративное качество студента-инженера, отсутствует заинтересованность в дальнейшем профессиональном развитии, негативное отношение, отсутствие собственных целей и интереса к изучению технических дисциплин (техническая безграмотность) и будущей профессии инженера, слабая сформированность специальных знаний, умений и навыков, которые не позволяют в полной мере выполнять поставленные задачи, отсутствие умений и навыков владения методами и механизмами творческого поиска, навыков организации самостоятельной деятельности, в процессе обучения не проявляются творческая активность, самостоятельность, слабое пространственное и структурное мышление будущих радистов, конструкторские умения и навыки на уровне исполнителя.
Студентам среднего уровня характерны: частичная сформированность отдельных компонентов профессиональной направленности, присутствует мотивация к профессиональной деятельности радиста, ситуативное проявление положительных мотивов; некоторые специальные графические знания, которые дают возможность определить направленность профессиональной деятельности и собственную стратегию поведения в различных ситуациях; знание отдельных, методов и механизмов изобретательской творческой деятельности. Низкий уровень самостоятельности. Конструкторские умения на уровне исполнителя, включают умение выполнять эскизы и рабочие чертежи деталей и сборочных чертежей, проекций, макетировать отдельные элементы изделий.
Высокий уровень характеризуется устойчивым развитием всех компонентов профессиональной направленности, студент-инженер выступает субъектом деятельности с устойчивыми профессиональными мотивами, интересом и сформированными профессионально значимыми качествами, наличием необходимых знаний и именно образовательных умений. Характеризуется наличием у студентов убеждения в необходимости дисциплины «Инженерная графика» и геометрических знаний и графических умений для профессиональной деятельности инженера. Развитая система знаний, выработка собственного стиля в области графики, творческое владение конструкторско-графическими умениями и средствами, развито пространственное и структурное мышление. Умение организовать самостоятельную исследовательскую и проектную деятельность инженера, умение критически оценивать результаты деятельности. Конструкторские умения на уровне руководителя проекта: поисковая исследовательская деятельность, проектирование базовой формы, разработка общего вида изделия, моделирование изделия, выбор соединений, подготовка текстовой документации, выполнение чертежей с помощью AutoCAD.
Выводы и перспективы дальнейших исследований. В работе обозначена совокупность критериев, показателей и охарактеризованы уровни сформированности профессиональной направленности студентов специальностей инженерного профиля в процессе изучения дисциплины «Инженерная графика». Исследование профессиональной направленности студентов проводилось на основе мотивационного, когнитивного и технологического критериев. Предложенные критерии, уровни и показатели сформированности могут обозначить возможность проведения мониторинговых исследований профессиональной направленности, что и является перспективой дальнейших поисков в этом направлении с целью определения путей повышения уровня профессиональной направленности будущих инженеров в высших технических учебных заведениях.
Проведенный анализ математической подготовки студентов инженерных специальностей показал широкие возможности для дальнейшего внедрения педагогической инноватики. Подводя итоги, заметим, что новейшие технологии и методики обучения математике являются одним из проявлений огромного потенциала инновационных процессов. Системное и последовательное их осуществление способствует углублению позитивных трансформаций в современном математическом образовании. Вместе с тем реализация нововведений на практике предполагает системную оценку эффективности процесса математической подготовки. Поэтому внедрение педагогических инноваций в практику всегда должно предполагать подготовительный этап, включающий в себя моделирование, экспертные оценки, экспериментальную проверку, дальнейшую доработку и соотношении с последними мировыми достижениями в области математического образования.



