Известно, что врачи в профессиональной деятельности нередко решают профессиональные задачи, используя методы математической статистики, теории вероятностей и др. Кроме того, при изучении студентами медицинских вузов ряда специальных дисциплин, например, таких как «Организация здравоохранения», «Эпидемиология» и др., необходимы не только теоретические знания в области математических наук, но и владение методами их применения [1].
Задачи медико-биологического содержания необходимо включить в профессионально важные разделы математики для того, чтобы:
- разрешить проблемную ситуацию медико-биологического характера,
- показать студентам-медикам взаимосвязи между: математикой и медицинской практикой, математикой и спецдисциплинами («Организация здравоохранения», «Эпидемиология» и др.);
- способствовать формированию первичных профессиональных умений будущих врачей, а именно формирование умений математически моделировать процесс или явление из медицинской практики.
Под задачами медико-биологического содержания мы понимаем текстовые задачи, сюжеты которых заимствованы из сферы профессиональной деятельности врача, а решения отыскиваются математическими средствами.
В задачах, описывающих медицинские ситуации, студенты имеют возможность анализировать исходные данные, сопоставлять конкретные медицинские категории с абстрактными вероятностно-статистическими понятиями, строить медико-биологические модели, осуществлять решение внутри модели. При этом они используют изученный по данной теме теоретический материал, что способствует его закреплению и лучшему усвоению. Перед выполнением таких задач студентам-медикам рекомендуется предварительно повторить смысл тех или иных медицинских терминов, используемых в условиях задачи. Каждое новое понятие в теории вероятностей и математической статистике требует закрепления базовых знаний студентов медицинских вузов, которое следует проводить методом математического моделирования. При этом осуществляются все этапы решения задач медико-биологического содержания: постановка цели, решение проблемы, выводы
Пример 1. Больному необходимо сделать переливание крови. Вероятность того, что группа крови определенного донора окажется подходящей, составляет Р(А) = 0,3. В центре переливания крови находятся пять доноров. Какое количество доноров подойдет для переливания крови данному больному?
Анализируя данные задачи студенты совместно с преподавателем переводят задачу с медицинского языка на математический, вводя обозначение (при этом определяют, что): случайная величина Х – число доноров в выборке, находящихся в центре переливания крови, имеющая следующие возможные значения: х1 = 0, х2 = 1, х3 = 2, х4 = 3, х5 = 4, х6 = 5. Студенты замечают, что случайная величина х1 = 0 говорит о том (значит то, что), что из данной выборки, т.е. пяти доноров, никто не подойдет для переливания крови больному; х2 = 1 – один из пяти подойдет; х3= 2 – два из пяти подойдут для переливания крови и т.д.
Внутримодельное решение. Студенты находят вероятности этих событий, т. е. вероятности того, что случайная величина примет каждое из своих возможных значений. Расчет искомых вероятностей студенты-медики выполняют по известной формуле Бернулли: ![]() , n = 5; p = 0,3;
, n = 5; p = 0,3;
q = 1 – 0,3 = 0,7. Подставляя в эту формулу данные задачи, получаем:
![]() ;
; ![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;![]() .
.
На основе полученных данных студенты-медики составляют ряд распределения (таблица 1).
Таблица 1
Распределение числа доноров в центре переливания крови
|
Х |
0 |
1 |
2 |
3 |
4 |
5 |
|
р |
0,168 |
0,360 |
0,309 |
0,132 |
0,028 |
0,002 |
Интерпретация полученных результатов. На основе составленного закона распределения студенты-медики делают вывод, что один донор из числа находившихся доноров в центре переливания крови подойдет больному, так как вероятность этого события, равная 0,36, – наибольшая.
Для того чтобы на старших курсах студентам-медикам было проще при решении профессионально-направленных задач по разделу медицинской статистики, на первом курсе при изучении темы «Основные понятия теории вероятностей» решаются задачи, аналогичные задачам по дисциплине «Организация здравоохранения», чтобы на старших курсах они могли воспользоваться и опираться на знания, полученные на первом курсе. На занятиях по математике студенты узнают, что одними из основных понятий теории вероятностей является абсолютная и относительная частота. Под абсолютной частотой на занятиях по математике они понимают число элементов совокупности, обладающих данным признаком, а под относительной частотой – отношение абсолютной частоты к общей совокупности, характеризующее интенсивность изучаемого явления. Данные понятия также используются на первых занятиях дисциплины «Организация здравоохранения», как абсолютная и относительная величина, студенты узнают, что для оценки изучаемых явлений, составляющих статистическую совокупность, используют статистические величины: абсолютные, относительные и средние величины.
Преподаватель дает студентам краткие теоретические сведения данных понятий, сопровождая примерами, тем самым студенты узнают, что абсолютные величины могут характеризовать размер изучаемых явлений и процессов. Так, например, абсолютная численность населения в Китае и Индии показывает, что эти две страны являются лидерами в мире по численности населения. Большое практическое значение для правильного планирования медицинской помощи населению имеют такие абсолютные величины, как численность населения и его отдельных возрастных и половых групп; численность медицинского персонала и лечебно-профилактических учреждений; количество больничных коек.
Однако, зная только абсолютные данные, мы не можем раскрыть состав, распространенность явления в данной среде. Поэтому в медицинской статистике для характеристики таких явлений, как заболеваемость, смертность, рождаемость и т. д. абсолютные величины переводятся в относительные: интенсивные, экстенсивные показатели, показатели соотношения и наглядности. Но при этом студенты-медики забывают тот пройденный материал первого курса по математической статистике и тем самым затрудняются в решении задач, похожих на задачи по статистике.
Приведем примеры задач, в которых представлена интеграция математических и медико-биологических знаний студентов медицинских вузов.
Пример 2. В городе D с численностью 73500 человек за год выявлено 860 случаев заболеваемости корью, в городе М с численностью 95200 человек было выявлено 980 человек, заболевших корью. Какова частота распространения данного заболевания в этих двух городах? [3].
При анализе задачи, сопоставив соответствующие данные, студенты-медики замечают, что по абсолютным данным заболеваемость корью в городе М выше, чем в городе D. Однако преподаватель подчеркивает, что и численность населения в городе М больше, чем в городе D. Поэтому для того чтобы решить поставленный вопрос в каком городе заболеваемость выше, необходимо в том и другом городе вычислить показатель интенсивности, т.е. показатель заболеваемости на 1000 жителей.
После всех рассуждений студенты-медики применяют уже известную им формулу вычисления интенсивного показателя. Таким образом, находят:
- частота распространения заболеваемости в городе D:![]() ;
;
- частота распространения заболеваемости в городе М:![]() .
.
В городе D из каждой 1000 заболевают 11,7 ‰; а в городе М – 10,3 ‰. Сравнивая полученные результаты, будущие врачи приходят к выводу, что частота распространения заболеваемостью корью в городе D выше, чем в городе М.
Пример 3. Рассчитать интенсивные, экстенсивные показатели. По полученным данным сделать соответствующие выводы. Численность города Н – 148000 человек. В 2005 году зарегистрировано 360 случаев инфекционных заболеваний, в том числе воздушно-капельных инфекций – 240, острых кишечных инфекций – 190, прочих – 60. Заболеваемость за предыдущие 3 года была следующей: 2002г. – 492,6 на 100 000 населения; 2003г. – 263,9 на 100 000 населения; 2004г. – 240,7 на 100 000 населения [5].
Для решения данной задачи рекомендуем студентам-медикам составить таблицу для удобства, то есть перевести задачу с медицинского языка на математический. Данные два понятия (интенсивный и экстенсивный показатели) встречаются на первых занятиях организации здравоохранения; преподаватель обращает внимание студентов-медиков на то, что при расчете интенсивных и экстенсивных показателей необходимо вспомнить формулу вычисления относительной частоты, которая служит основой для расчета данных показателей, в чем и проявляется связь медицинского раздела с математикой.
Пример 4. В В-ском районе численность населения 75000 человек. В поликлиниках района зарегистрировано 4500 случаев заболеваний кожи. Рассчитать коэффициент распространенности заболевания.
При решении данной задачи преподаватель знакомит студентов-медиков с понятием «коэффициент распространенности заболевания» - это доля населения, страдающая данным заболеванием в определенный момент времени [4].
Коэффициент распространенности заболеванием равен отношению числа лиц, страдающих данным заболеванием в определенный момент времени к численности данной группы населения в это же время. Таким образом, студенты замечают, что вычисление данного коэффициента основано на формуле относительной частоты.
В итоге нами был проведен констатирующий эксперимент на базе Астраханского государственного медицинского университета, в котором участвовали студенты старших курсов и преподаватели специальных дисциплин, анкетирование и опрос которых показал, что после изучения математики доля студентов экспериментальной группы, считающих, что математическая подготовка необходима будущему врачу, и имеющих представление о том, где математические знания могут ими использоваться в дальнейшей профессиональной деятельности, значительно превышает долю таких студентов в контрольной группе. Таким образом, большинство студентов экспериментальных групп рассматривают математику как важный компонент их профессионального образования.
Мы пришли к выводу, что необходимо разработать методику обучения студентов-медиков математическим основам медико-биологических знаний, учитывающей специфику вуза, уровень знаний и умений, затруднения каждого студента.
Совместно с коллективом кафедры «Физика, математика и медицинская информатика» были разработаны учебно-методические пособия: задачник «Элементы теории вероятностей и математической статистики», содержащий в основном задачи медико-биологического характера; «Рабочая тетрадь по элементам теории вероятностей и математической статистики для студентов медицинских специальностей»; «Методические рекомендации для студентов-медиков к лабораторным работам по математической статистике».
Занятия по теории вероятностей и математической статистике в контрольной группе проводились по традиционной методике, а в экспериментальной группе – с использованием методики комплексного подхода к обучению математическим основам медико-биологических знаний студентов медицинских вузов. Об эффективности разработанной методики мы судили по трем показателям, а именно, по сформированности умений: - решать профессиональные задачи; - по исходным данным составлять задачи медико-биологического содержания; - составлять опорные схемы по содержанию теоретического фрагмента.
Результаты сравнительной динамики уровня сформированности умений представлены на диаграммах (рисунок). Из этих диаграмм видно, что в ходе эксперимента уровень обученности по математике в экспериментальной группе значительно вырос по сравнению с доэкспериментальным. У студентов контрольной группы изменения незначительны.
Контрольная группа
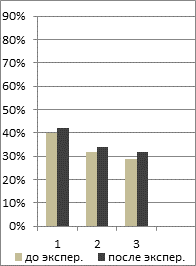
Экспериментальная группа
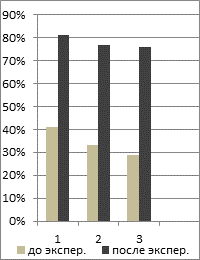
Результаты уровней сформированности умений: 1 - решать профессиональные задачи; 2 – составлять задачи медико-биологического содержания; 3 - составлять опорные схемы студентов-медиков до и после эксперимента
Полученные в ходе экспериментальной работы результаты свидетельствуют о том, что разработанная методика комплексного подхода к обучению математическим основам медико-биологических знаний студентов медицинских вузов является более эффективной, чем традиционная, как в плане математической подготовки студентов, так и в плане применения математических знаний при решении медико-биологических задач [2].
Мы пришли к выводу, для того чтобы скоординировать знания по математике и спецдисциплинам, необходимо при изучении математике предлагать задачи, моделирующие профессиональную деятельность будущего врача. Тогда многие студенты, не будут затрудняться при решении задач медико-биологического содержания, в сюжетах которых они могут увидеть уже знакомые им математические задачи. Более того, при решении рассмотренных задач у студентов-медиков закрепляются не только абстрактные теоретико-вероятностные понятия и алгоритм их вычисления, но и их медико-биологический смысл.
Рецензенты:
Мирзабекова О.В., д.п.н., доцент, заведующий кафедрой физики, математики и медицинской информатики ГБОУ ВПО «Астраханский государственный медицинский университет» Минздрава РФ, г. Астрахань.
Ильязова М.Д., д.п.н., доцент, профессор кафедры социологии и психологии ФГБОУ ВПО «Астраханский государственный технический университет», г. Астрахань.



