Анализ осложнений показывает необходимость разработки эффективных методов управления работой фонда скважин. Кроме того, разработка и эксплуатация нефтяных месторождений в осложнённых условиях нуждается в развитии определённых форм обслуживания, обуславливающих повышение эффективности нефтедобычи. При этом важно оценить существующие техники и технологии, определить основные направления и задачи их совершенствования. Высокая надежность нефтепромысловых систем и малый объём ремонтных работ способствуют увеличению межремонтного периода и коэффициента эксплуатации скважин, создают благоприятные условия в организации и управлении процессом нефтедобычи.
Важнейшей задачей современного этапа развития нефтегазодобывающей промышленности является задача оптимального назначения ремонтных бригад на проведение ТОР скважин и планирования сроков их проведения.
Таким образом, оптимальный подбор назначений ремонтных бригад на проведение ТОР должен быть достигнут за счет максимизации или минимизации определенной меры эффективности назначения: прибыли, стоимости, затрат и т.д. Для каждого потенциального назначения оценивается мера эффективности.
Решению задачи об организации ремонтных работ на скважинах может быть реализовано с помощью прямо-двойственного алгоритма Хичкока-АЛЬФАБЕТА, алгоритма Дейкстры, метода Жадного алгоритма на пересечении взвешенных матроидов, алгоритма Флойда, метода взвешенного паросочетания [1, 2].
Данные методы основаны на построении сетевой модели. Для создания модели рассмотрим некоторый участок месторождения. Количество добывающих скважин составляет n, дебиты скважин равны ![]() (i=1, …, n1). В центре расположена база, к которой относится m ремонтных бригад, прямыми линиями будет изображена сеть дорог, связывающая кусты и базу между собой.
(i=1, …, n1). В центре расположена база, к которой относится m ремонтных бригад, прямыми линиями будет изображена сеть дорог, связывающая кусты и базу между собой.
Существует необходимость в постоянном поддержании скважинного оборудования в работоспособном состоянии. В связи с этим составляется план-график проведения технического обслуживания и ремонта скважин. При этом учитывается, что каждая бригада может обслуживать только одну скважину и переходить на обслуживание другой только после завершения ремонта на предыдущей скважине. Отказавшую скважину либо ремонтируют, если имеется хотя бы одна свободная бригада, либо выстраивают в очередь. Отремонтированная скважина начинает работать.
Для эффективного назначения ремонтных бригад на скважины в качестве оптимизирующих параметров рассматриваются:
1) время межремонтного периода;
2) дебит скважины до и после ремонта;
3) количество ремонтных бригад;
4) расстояние, на котором находится ремонтная бригада от требующей ремонта скважины.
В связи с тем, что число ремонтных бригад ограничено, очерёдность проведения планово-профилактических мероприятий в течение оптимального периода составляется с учётом расстояний между скважинами и их дебитов. При этом приоритет отдаётся скважине с максимальным дебитом, находящейся на кратчайшем расстоянии от ремонтной бригады.
Так как одним из параметров оптимизации является расстояние от бригады до скважины, то данная задача представляется как экстремальная задача на графах. В данном случае вершинами графа являются кусты, а рёбрами – дороги. В качестве весов рёбер используются расстояния между скважинами. Таким образом, задача сводится к определению кратчайшего пути при обходе всех скважин.
Определение кратчайшего расстояния производится с помощью жадного алгоритма. Для этого задаётся матрица расстояний между кустами и базой. В результате расчёта получены минимальные остовные деревья, которые и являются кратчайшими путями при обходе всех скважин.
Приведём алгоритм, который работает для произвольного взвешенного матроида. Его работу легко будет понять из блок-схемы (рис. 1).
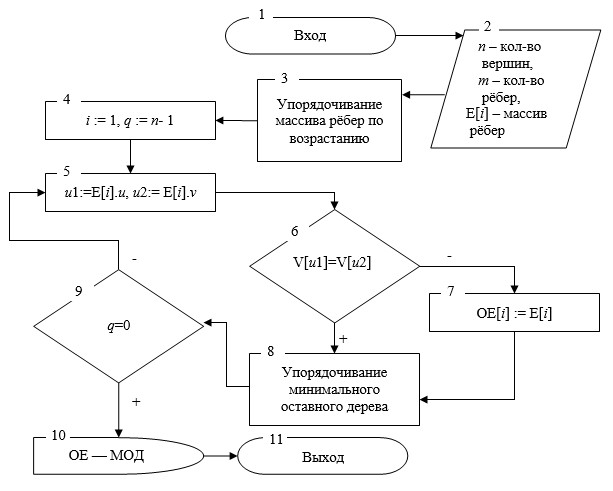
Рис. 1. Блок-схема жадного алгоритма
В качестве входных данных в этом алгоритме выступает взвешенный графический матроид M=(Е,I) и связанная с ним весовая функция. Алгоритм возвращает оптимальное подмножество ОЕ – минимальное остовное дерево.
Для повышения эффективности работы бригад требуется составить очередность проведения планово-профилактических мероприятий в течение периода оптимального ремонта, учитывая расстояние между скважинами и их дебиты. Приоритет отдается скважине с максимальным дебитом, находящейся на кратчайшем расстоянии от ремонтной бригады. Расчет производится с помощью методов целочисленного линейного программирования. Алгоритм для нахождения минимальных расстояний между ремонтной базой и скважинами легко понять из блок-схемы, представленной на рис. 2.
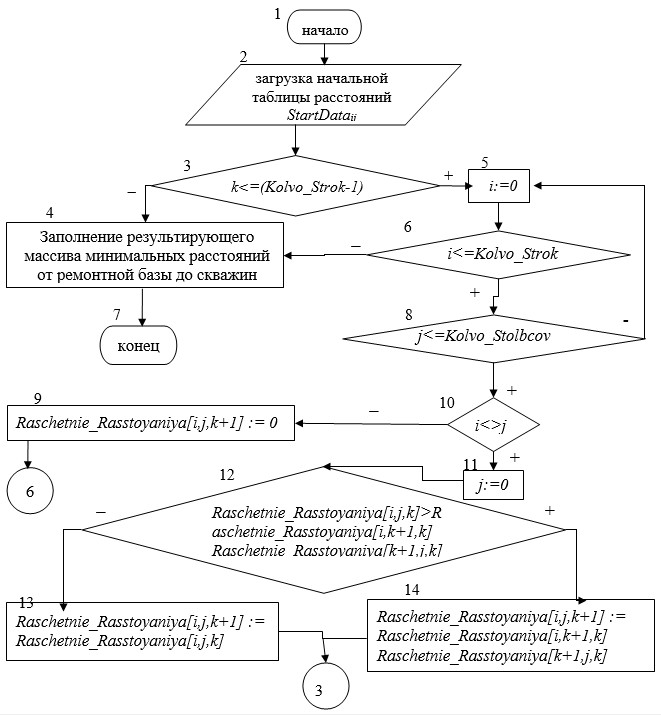
Рис. 2. Блок-схема алгоритма Флойда
Задачу о назначениях можно описать как упрощенную задачу линейного программирования, являющуюся частным случаем задачи Хичкока, и поэтому ее можно решать, применяя венгерский метод. Венгерский метод оптимизирует распределение ремонтных бригад на основе их типов, кратчайших расстояний от базы до скважин и обратно.
В качестве графа может быть взята произвольная схема, ребрами которого являются дороги. Предлагаемый способ решения позволяет классифицировать ремонтные бригады при их назначении на скважины и дороги транспортной сети могут быть с двусторонним движением.
р(х) = (кратчайшая длина пути из s в х, в котором все промежуточные вершины принадлежат W).
p(y)= тiп{р(у), р(х)+сху} для всех y![]() W.
W.
Данное выражение показывает, что либо р(у) для y![]() W не изменяется при добавлении х к W, либо новое р(у) равняется кратчайшему расстоянию от s до х по вершинам из W плюс, расстояние непосредственно от х до у.
W не изменяется при добавлении х к W, либо новое р(у) равняется кратчайшему расстоянию от s до х по вершинам из W плюс, расстояние непосредственно от х до у.
Таким образом, задачу можно сформулировать в виде задачи линейного программирования (ЛП).
Пусть даны m, n![]() Z+,запасы ai
Z+,запасы ai![]() R+(i=1, …, m) в пунктах отправления, потребности
R+(i=1, …, m) в пунктах отправления, потребности
bj![]() R+(j=1, ..., п) в пунктах назначения и cij
R+(j=1, ..., п) в пунктах назначения и cij![]() R+ (i=1, ..., m и j=1, ..., п). Индивидуальной задачей Хичкока является следующая задача ЛП с переменными fij:
R+ (i=1, ..., m и j=1, ..., п). Индивидуальной задачей Хичкока является следующая задача ЛП с переменными fij:
min![]()
![]()
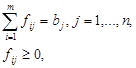
где ![]() .
.
Однако данные равенства не приводят к потере общности, поскольку всегда можно ввести фиктивный ![]() пункт назначения с потребностью:
пункт назначения с потребностью:
![]()
и стоимостями ci,n+1=0, i=l, ..., т.
Использование алгоритма Альфабета позволяет оптимизировать распределение и обслуживание заявок при следующих критериях: минимальные затраты, максимум прибыли предприятия.
Одной из основных задач сервисной службы всех подразделений является обслуживание и обеспечение надежной, бесперебойной работы скважин.
Задача состоит в оптимизации распределения и обслуживания заявок при заданном плане добычи нефти при минимальных затратах на его выполнение или при максимуме прибыли предприятия. Пусть на склад, через определенный промежуток времени, поступают заявки с цехов о потребности в том или ином оборудовании. Необходимо развести оборудование на цеха через базы с учетом 25 %-го резерва. Рассмотрим заявку, поступившую на склад: требуется оборудование для ремонта.
Для решения данной задачи использован алгоритм для задачи Хичкока – АЛЬФАБЕТА. Таким образом, данную задачу (рис. 3) можно представить как экстремальную задачу на графах. В частности, если представить цеха и базы вершинами графа, а дороги к ним – дугами графа с определенными весами (расстояние или стоимость), то задача сводится к определению оптимального пути при обходе и обслуживании всех цехов.

Рис. 3. Схема расположения сервисной службы
Выводы и предложения:
1. Уменьшение непроизводительных работ и простоев, обусловленных в основном организационно-техническими причинами и нарушениями трудовой дисциплины, является резервом снижения затрат времени на проведение ремонта.
2. Необходимо разрабатывать новые методы и способы организации ремонтно-восстановительных работ, позволяющих оптимизировать графики назначения ремонтных бригад на скважины для повышения эффективности их работы.
3. Разработаны методики назначения ремонтных бригад на скважины и план-график проведения технического обслуживания и ремонта скважин с учетом приоритетов.
Рецензенты:
Грачев С.И., д.т.н., профессор, заведующий кафедрой «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ТюмГНГУ, г. Тюмень;
Сохошко С.К., д.т.н., заведующий кафедрой «Моделирование и управление процессами нефтегазодобычи», Институт геологии и нефтегазодобычи, ФГБОУ ТюмГНГУ, г. Тюмень.



