Метрологические характеристики автономных средств измерений, предназначенных для хранения, воспроизведения и передачи размера единиц величин, изменяются в процессе эксплуатации. В дальнейшем будем говорить об эволюции основной погрешности Δ(t), подразумевая, что вместо нее может быть аналогичным образом рассмотрена любая другая метрологическая характеристика.
Следует отметить, что не все составляющие погрешности подвержены эволюции во времени. Например, методические погрешности зависят только от используемой методики измерения. Среди инструментальных погрешностей есть много составляющих, практически не подверженных старению [1-3], например размер кванта в цифровых приборах и определяемая им погрешность квантования.
Эволюция метрологических характеристик средств измерений во времени обусловлена процессами старения в его узлах и элементах, вызванными взаимодействием с внешней окружающей средой. Эти процессы протекают в основном на молекулярном уровне и не зависят от того, находится ли средство измерения в эксплуатации или хранится на консервации. Следовательно, основным фактором, определяющим старение средств измерений, является календарное время, прошедшее с момента их изготовления, т.е. возраст. Скорость старения зависит, прежде всего, от используемых материалов и технологий. Исследования [4] показали, что необратимые процессы, изменяющие погрешность, протекают очень медленно и зафиксировать эти изменения в ходе эксперимента в большинстве случаев невозможно. В связи с этим большое значение приобретают различные математические методы, на основе которых строятся модели эволюции погрешностей и производится прогнозирование метрологических отказов.
Цель работы: исследование математических моделей утраты средствами измерений свойств, заданных при проектировании и изготовлении. Физико-химические процессы, приводящие к отказам, можно классифицировать по различным признакам. Так как в основе потери работоспособности средств измерений всегда лежат физико-химические закономерности, то чем глубже они изучены, тем полнее информация о поведении метрологических характеристик.
Модели эволюции метрологических характеристик
В [1] рассмотрены основные физико-химические процессы, которые считаются ответственными за изменение свойств материалов и, как следствие, за эволюцию метрологических характеристик средств измерений, предназначенных для хранения, воспроизведения и передачи размера единиц величин. Это диффузионные и химические процессы, распад твердых растворов, раскристаллизация твердого тела, изменение механических и электрических свойств твердых тел. Законы эволюции метрологических характеристик, описывающих названные процессы, характеризуются различными математическими зависимостями, как правило, нелинейными и являются стохастическими.
Диффузионные процессы описываются дифференциальными уравнениями в частных производных, например известным законом Фика [1; 2]. Химические процессы описываются обыкновенными дифференциальными уравнениями и уравнениями в частных производных. Химические процессы зависят от условий, в которых протекают химические реакции. Так, например, влияние температуры характеризуется законом Аррениуса [1]. Модели распада твердых растворов и раскристаллизация твердых тел описываются экспоненциальными зависимостями и обыкновенными дифференциальными уравнениями и уравнениями в частных производных. Аналогичные зависимости описывают процессы изменения механических и электрических свойств составных частей средств измерений. На все эти процессы оказывают существенное влияние внешние воздействия (условия эксплуатации, температура, давление, электрические поля и т.д.).
Таким образом, математические модели физико-химических процессов, приводящих к изменениям свойств материалов, из которых изготавливаются средства измерений, предназначенные для хранения единиц величин, должны учитывать векторный параметр, характеризующий условия эксплуатации, влияние внешней среды, начальные и граничные состояния средств измерений и т.д. В данных моделях часто используются дифференциальные уравнения: обыкновенные, в частных производных, стохастические и др.
эволюция погрешности средств измерений во времени представляет собой нестационарный случайный процесс. Множество его реализаций показаны на рис. 1 в виде кривых модулей погрешности.
В каждый момент tj они характеризуются некоторым законом распределения плот-ности вероятности р(Δ, tj) (кривые 1 и 2 на рис. 1а). В центре полосы (кривая Δср(t)) наблюдается наибольшая плотность распределения погрешностей, которая постепенно уменьшается к границам полосы Δd, теоретически стремясь к нулю при бесконечном удалении от центра. Верхняя и нижняя границы полосы погрешностей средства измерений могут быть представлены в виде некоторых квантильных границ, внутри которых заключена большая часть погрешностей, реализуемых с доверительной вероятностью Р(Δd, - Δd). За пределами границ с вероятностью (1 - Р(Δd, -Δd))/2 находятся погрешности наиболее удаленные от центра реализаций.
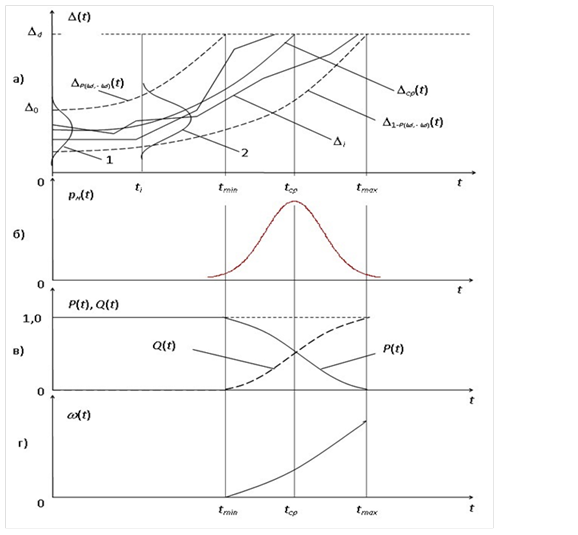
Рис. 1. Модель эволюции погрешности во времени (а), плотность распределения времени наступления метрологических отказов (б), вероятность безотказной работы (в) и зависимость интенсивности метрологических отказов от времени (г)
Для оценки состояния средства измерений в будущие моменты времени необходимо выбрать модель эволюции его метрологических характеристик. В классе экстраполяционных методов изменения можно использовать модели, построенные на основе монотонных, комбинированных или диффузионных процессов [4-9]. Нужно отметить, что расхождение в оценке изменяющихся метрологических характеристик может достигать существенного значения при использовании различных моделей. Поэтому к выбору модели следует подходить с позиций точности и адекватности описания реальных процессов.
Наиболее простой моделью, удовлетворяющей в основном этим условиям, является линейная модель, в которой процесс эволюции метрологических характеристик аппроксимируется линейной случайной функцией
![]() , (1)
, (1)
где x0 и z – в общем случае случайные величины.
Причем здесь могут быть различные модификации: веерная с нулевым начальным разбросом, веерная с ненулевым начальным разбросом, равномерная. Более сложными моделями являются те, в которых используются нелинейные функции. Среди нелинейных моделей наиболее часто встречаются экспоненциальная
![]() , (2)
, (2)
и параболическая
![]() . (3)
. (3)
Реже используются другие модели вида
![]() ,
, ![]() ,
,
![]() ,
,![]() , (4)
, (4)
где z1, z2, z3, z4 – постоянные коэффициенты.
Эти и другие модели описывают монотонные процессы, характерной особенностью которых является то, что производная не меняет знак и, следовательно, граница допустимой области может быть пересечена один только раз. Данными моделями описываются необратимые процессы износа, коррозии, усталость материалов и некоторые другие.
Поведение изменяющихся метрологических характеристик можно моделировать комбинированным процессом, представляющим собой сумму монотонного и нормального стационарного процесса с нулевым математическим ожиданием и постоянной дисперсией. Такая ситуация имеет место, когда разброс значений исследуемого параметра около некоторой средней зависимости соответствует одному и тому же стационарному шуму, обусловленному колебаниями эксплуатационных нагрузок, погрешностями измерения, локальными свойствами материалов и так далее. Развитие вышеуказанных моделей предложено в [1]. Их основной особенностью является то, что модели связывают законы распределения случайного процесса изменения работоспособности с его поведением.
В настоящее время все чаще применяются модели, использующие диффузионные марковские процессы [1-3]. В основе таких моделей лежит стохастическое дифференциальное уравнение
![]() , (5)
, (5)
где f(x,t) – коэффициент сноса; g(x,t) – коэффициент диффузии марковского процесса;
wt – винеровский процесс.
Коэффициент сноса характеризует среднее значение локальной скорости, а коэффициент диффузии – локальную скорость изменения дисперсии приращения марковского процесса.
Данные модели применимы в тех случаях, когда случайный процесс эволюции метрологических характеристик может быть достаточно адекватно описан диффузионным марковским процессом. Применение диффузионных марковских процессов обусловлено их свойствами, основное из которых – это отсутствие последействия: при эволюции метрологических характеристик средств измерений существенным является знание состояния процесса эволюции метрологических характеристик в настоящий момент времени. Поведение диффузионного марковского процесса полностью описывается его локальными характеристиками, то есть коэффициентом сноса и коэффициентом диффузии. Модель эволюции метрологических характеристик, использующая диффузионные марковские процессы, наиболее адекватна исследуемому процессу и универсальна по сравнению с другими, используемыми в теории случайных функций. Сравнительный анализ, показывающий преимущество моделей эволюции метрологических характеристик в виде диффузионного марковского процесса, по сравнению с другими моделями, подробно описан в [3].
Выводы
Модель, используемая для успешного решения задачи описания процесса эволюции метрологических характеристик средств измерений, должна отвечать следующим основным требованиям:
- удобство для использования. Процессы измерений, вычислений, обработки результатов при решении задач прогноза должны быть максимально приспособлены для выполнения их оператором, не имеющим специальных навыков;
- использование наиболее совершенного и достаточно хорошо разработанного математического аппарата;
- универсальность. Модель должна описывать как стационарные, так и нестационарные процессы;
- возможность использования дополнительных критериев для оценки объективности выбора параметров модели;
- возможность корректировки модели и полученных результатов при поступлении дополнительной информации о характере процесса;
- удобство формального описания параметров изменяющегося процесса, минимизация ограничений при моделировании;
- адекватность изменяющемуся процессу. В модели должна учитываться физическая сущность изменяющегося процесса;
- достаточно высокая точность получения результата. Возможность получения решения задачи описания процесса не только в вероятностном, но и в аналитическом виде;
- обеспечение оперативности получения результата, возможность предварительного создания баз данных, простота использования вычислительной техники;
- обеспечение возможности решения как прямой, так и обратной задачи описания процесса;
- устойчивость к случайным выбросам результатов и другим возмущениям.
Всем перечисленным требованиям наиболее соответствуют диффузионные марковские модели. Именно они используются в работе для обоснования методов описания процесса эволюции метрологических характеристик средств измерений.
Рецензенты:
Звездина М.Ю., д.ф.-м.н., доцент, зав. кафедрой «Радиоэлектроника», Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Донской государственный технический университет» Минобрнауки России, г. Ростов-на-Дону;
Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, Федеральный научно-производственный центр ФГУП «РНИИРС», г. Ростов-на-Дону.



