В работе [1] описано наблюдавшееся в эксперименте разделение твёрдых частиц в вертикальном столбе жидкости, совершающем крутильные колебания. Отмечено, что частицы, имевшие меньшие размеры и большую плотность, собирались у стенки сосуда, совершавшего крутильные колебания и передававшего их жидкости, а частицы, имевшие большие размеры и меньшую плотность, концентрировались в центральной, осевой части сосуда. При стационарном вращении столба жидкости разделения частиц не наблюдалось, все они собирались у стенки сосуда.
Для раскрытия механизма разделения твёрдых частиц в столбе жидкости, совершающем крутильные колебания, рассмотрим особенности динамики твёрдых частиц, находящихся под действием нестационарных центробежных сил.
В рассматриваемой ситуации на находящиеся в жидкости твёрдые частицы в радиальном, горизонтальном направлении действуют следующие силы:
1) направленная по радиусу от оси вращения центробежная сила инерции:
![]() , (1)
, (1)
где ![]() масса частицы;
масса частицы; ![]() угловая скорость частицы;
угловая скорость частицы; ![]() радиус вращения частицы;
радиус вращения частицы;
2) направленная по радиусу к оси вращения центробежная архимедова сила
![]() , (2)
, (2)
где ![]() масса жидкости, вытесненной частицей;
масса жидкости, вытесненной частицей; ![]() угловая скорость слоев жидкости;
угловая скорость слоев жидкости;
3) направленная по радиусу против скорости радиального перемещения ![]() частицы сила вязкого сопротивления, которая в силу малости размеров частиц определяется законом Стокса:
частицы сила вязкого сопротивления, которая в силу малости размеров частиц определяется законом Стокса:
![]() , (3)
, (3)
где k – коэффициент сопротивления движению частицы, зависящий от вязких свойств жидкости, размеров и формы частицы.
Уравнение динамики радиального движения частицы запишется в виде:
![]() , (4)
, (4)
где ![]() ускорение радиального движения частицы.
ускорение радиального движения частицы.
Из уравнения (4) получаем
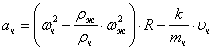 , (5)
, (5)
где ![]() плотность жидкости, а
плотность жидкости, а ![]() плотность частицы.
плотность частицы.
Из уравнения (5) вытекает, что в начальный момент времени, когда ![]() при
при 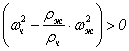 ускорение частицы направлено от оси сосуда к его стенке, а при
ускорение частицы направлено от оси сосуда к его стенке, а при 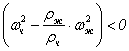 ускорение частицы направлено к оси сосуда.
ускорение частицы направлено к оси сосуда.
Значит, при 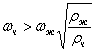 твёрдая частица должна двигаться к стенке сосуда, а при
твёрдая частица должна двигаться к стенке сосуда, а при 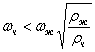 - к оси сосуда.
- к оси сосуда.
Связь между угловыми скоростями частицы ![]() и слоёв жидкости
и слоёв жидкости ![]() найдём исходя из закона сохранения механической энергии, приняв, что кинетическая энергия колебательного движения твёрдых частиц приобретается ими за счёт работы вязких сил, действующих на них со стороны жидкости.
найдём исходя из закона сохранения механической энергии, приняв, что кинетическая энергия колебательного движения твёрдых частиц приобретается ими за счёт работы вязких сил, действующих на них со стороны жидкости.
Пусть ![]() меняется со временем по закону:
меняется со временем по закону:
![]() , (6)
, (6)
где a-угловая амплитуда колебаний, f- линейная частота колебаний, t- текущее время
Тогда полученное из закона сохранения энергии дифференциальное уравнение для нахождения ![]() будет иметь вид:
будет иметь вид:
![]() , (7)
, (7)
а его решение, согласно [2], для установившихся колебаний
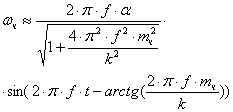 . (8)
. (8)
Из уравнения (8) следует, что угловая скорость твёрдой частицы будет меняться со временем по тому же гармоническому закону, что и угловая скорость частиц жидкости, но с некоторым отставанием по фазе. При этом амплитудное значение угловой скорости твёрдой частицы будет всегда меньше амплитудного значения угловой скорости частиц жидкости.
Разница между амплитудными значениями скоростей слоев жидкости и твердых частиц и разность фаз их колебаний будет определяться соотношением между массовыми и вязкими силами, действующими на твердые частицы, они тем больше, чем сильнее влияние массовых сил.
Частицы, испытывающие преимущественное действие вязких сил, устойчиво движутся от оси вращения, а частицы, для которых более существенно действие массовых сил, движутся с ускорением, направленным к этой оси.
СПИСОК ЛИТЕРАТУРЫ
1. Фатьянов А.В., Машеренков В.М., Никитина Л.Г. Прогнозирование эффективности разделения минеральных частиц в нестационарном центробежном поле. Пятая междунар. конф.: Новые идеи в науках о Земле. Материалы конф. Часть II.-М., 2001.
2. Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. – М., 1976. -576 с.



