В основе инновационного подхода к отбору содержания предметной подготовки учителя математики в условиях модернизации лежит овладение когнитивным стилем профессиональной деятельности посредством актуализации субъективного опыта в процессе освоения теоретического обобщения базовых учебных элементов школьной математики (БУЭШМ) на основе процессов фундирования опыта личности и наглядного моделирования математических объектов и процессов [3]. Педагогическая технология представляет собой существо совместной деятельности преподавателя и студента, ведущее к достижению планируемых и вероятностно гарантированных результатов обучения. В то же время методическое оформление сути технологического процесса придает технологии гибкость и определяется, в частности, как содержанием учебной информации, так и педагогическим мастерством преподавателя. ФГОС ВПО третьего поколения дают вузам широкие возможности получения результатов обучения в контексте проектирования авторских, региональных учебных планов и программ, отражающих специфику региона, научно-методические предпочтения профессорско-преподавательского состава, технические возможности учебного заведения. Однако в реальной жизни вузовские разработки сводятся, как правило, к традиционному наполнению содержания профессиональной подготовки, апробированному набору учебных предметов и их объему в структуре учебных планов ( к сожалению, проявление этой тенденции относится не только к высшей, но и к средней школе). Технологические конструкты концепции фундирования, разработанной В.Д. Шадриковым и Е.И.Смирновым, представленные в настоящей статье, дают реальные возможности для конкретного вуза выстраивать инновационные образовательные конструкты с новой структурой и содержанием профессиональной подготовки, опирающиеся на уже апробированные теории и технологии профессионального образования [5]. Уникальный опыт Ярославского госпедуниверситета им. К.Д. Ушинского по реализации инновационного содержания профессиональной подготовки будущего учителя математики в рамках экспериментального образовательного стандарта по специальности «математика» (Приказ № 2046 от 14.05.2001 г., МО РФ). в период с 2001 по 2006 гг. показал высокую эффективность разработанной технологии и возможность ее переноса в новые условия профессионального образования [6].
В ходе психологического эксперимента, проведенного Ю.П. Поваренковым и М.Г. Угаровой, были получены следующие основополагающие результаты:
* студенты контрольной группы в большей степени ориентированы на заботу о собственном здоровье, установление близких отношений с людьми, интересную работу и творческую реализацию. Значимость данных ценностей для студентов, обучавшихся по стандартной программе, подчеркивает ориентацию студентов на традиционные ценности, реалистичность их взглядов. Студенты экспериментальной группы, обучавшиеся по программе с применением технологии фундирования, более уверены в себе, ориентированы на переживание прекрасного в природе и искусстве; стремятся к уважению окружающих, коллектива, к максимально полному использованию своих возможностей, сил и способностей; активнее используют возможность расширения своего образования, кругозора, общей культуры, интеллекта; для них значимы благосостояние, развитие и совершенствование других людей. Можно сделать вывод, что студенты, обучавшиеся по программе с применением технологии фундирования, в большей степени ориентируются на гуманистические ценности, ориентированы на развитие собственной личности; система ценностей этих студентов идеалистична. Несмотря на выделенные проблемные области в ценностной сфере студентов, общая гуманистическая направленность может сыграть положительную роль в реализации студентов в педагогической деятельности;
* студентов контрольной группы можно охарактеризовать как более способных действовать самостоятельно, решительно, правдивых, искренних. У них в большей степени развиты чувство долга, умение держать свое слово. Студенты, обучавшиеся по программе с применением технологии фундирования, характеризуются большей критичностью к себе и окружающим людям, высокими требованиями к жизни и высокими притязаниями;
* профессиональная направленность студентов обеих групп характеризуется средним уровнем однородности и низким уровнем дифференцированности профессиональных предпочтений, что свидетельствует о незавершенности профессионального самоопределения и существовании проблемы выбора сферы профессиональной реализации и места будущей работы. Выявленные значимые различия свидетельствуют о том, что студенты, обучающиеся по программе с применением технологии фундирования, в большей степени склонны к выбору профессии педагога в качестве сферы профессиональной деятельности;
* рассматривая отличия в профессиональной самооценке студентов, обучавшихся по разным программам, следует отметить, что самооценка студентов, обучавшихся по стандартной программе, выше, чем у студентов, обучавшихся по программе с применением технологии фундирования. На наш взгляд, полученные результаты объясняются тем, что студенты, обучавшиеся по стандартной программе, завышают свою самооценку, а студенты, обучавшиеся по программе с применением технологии фундирования, более критично относятся к себе. Эта группа студентов видит меньше возможностей для реализации ценностей, поэтому в меньшей степени удовлетворена своей профессиональной позицией; студенты, обучавшиеся по программе с применением технологии фундирования, более критичны к себе как к профессионалу, что дает возможность четче видеть собственные недостатки и работать над их устранением;
* студенты, обучавшиеся по программе с применением технологии фундирования, отличаются более высоким уровнем развития математических способностей, необходимых для успешной деятельности учителя математики, а также более высоким прогнозом успешности в профессиональной деятельности.
Контрольные срезы по математической подготовленности студентов контрольной и экспериментальной групп показали значимые позитивные сдвиги студентов экспериментальной группы, обучающейся по экспериментальной программе на основе концепции фундирования. В итоге треть студентов экспериментальной группы закончила вуз с отличием ( что превышает среднестатистические показатели выпускников физико-математического факультета за последнее десятилетие в ЯГПУ на 20%). Более того, 25% выпускников продолжили профессиональное педагогическое образование (аспирантура, соискательство, реальная работа в вузах, менеджмент в системе общего образования) с элементами исследовательской деятельности.
Цель исследования
Как показывает анализ состояния высшего педагогического образования, проведенный выше, недостаток или полное отсутствие обоснованной методологической базы при определении содержания профессионального образования приводят к тому, что новое содержание мало чем отличается от прежней специальной подготовки. В то же время уменьшенный объем предметной подготовки, слабая профессионализация, практическое разрушение системы профессионального отбора приведут к углублению кризисов и противоречий в подготовке педагога. Поэтому цель настоящего исследования предполагает выявление технологических конструктов концепции фундирования, которые определяют тенденции реализации, когда в основной образовательной программе вуза должны быть формализованы и материализованы в виде конкретных учебных дисциплин, средств и форм учебной деятельности не только обоснованные методологически дидактические (когнитивные) процессы, формирующие целеполагание, приобретение, применение и преобразование опыта личности, но также адаптационные процессы, характеризующие технологические профессиональные пробы принятия студентом профессии учителя и личностные процессы, направленные на проявление особенностей и развитие мотиваций и эмоций, рефлексии и саморегуляции, самооценки и выбора, интеллекта и креативности личности.
Методология, методы и технологические конструкты
Типология образовательных процессов проектирует триаду модулей в проектировании ГОС высшего педагогического образования: дидактический, адаптационный, гуманитарный. При этом дисциплины предметной подготовки должны образовывать единый комплекс в направлении фундаментализации и профессионализации педагогического процесса. В соответствии с концепцией фундирования основу для этого в виде интегративных конструктов базовых учебных элементов школьной математики (БУЭШМ) составляют 7 содержательных линий: числовая, функциональная, геометрическая, тождественных преобразований, уравнений и неравенств, стохастическая и алгоритмическая. Каждая содержательная линия определяет базовые знания, умения, навыки и методы вузовской математики, распределенные по оптимальному набору учебных предметов и дисциплин. Так, учебный предмет, представляя собой целостную структуру учебной информации в составе теоретического, практического, прикладного, деятельностного, эвристического и гуманитарного компонентов, разворачивается в базисном (содержательном), процессуальном и иерархическом уровнях в своих локальных, модульных и глобальных проявлениях.
В развертывании содержания учебного предмета в контексте профессионализации фундирования БУЭШМ с особой отчетливостью прослеживаются три линии:
1) логика определения содержания учебного предмета исходя из его особенностей: отбор базовых учебных элементов, структуры, этапы изучения, интегративные знания, соотношение теоретического и практического компонентов и т.п.;
2) логика преемственности и содержания теоретического обобщения БУЭШМ: содержательные линии школьной математики и набор учебных предметов вузовского обучения, построение системы логически взаимосвязанных видовых проявлений базовых родовых понятий, усиление прикладного и деятельностного компонентов обучения математике, модульный принцип развертывания содержания учебного предмета и т.п.;
3) учет психологических и педагогических особенностей восприятия, усвоения, представления, применения, анализа и синтеза учебного материала субъектом обучения: наглядное моделирование, имитационное моделирование, структурный анализ базовых учебных элементов, усиление эвристического и гуманитарного компонентов, развитие интеллектуальных и личностных характеристик, вариативность решения учебных задач, взаимопереходы знаковых систем и т.п.
В основе инновационного подхода к отбору содержания предметной подготовки учителя математики лежит овладение когнитивным стилем профессиональной деятельности посредством актуализации субъективного опыта в процессе освоения теоретического обобщения БУЭШМ на основе процессов фундирования и наглядного моделирования. Педагогическая технология представляет собой существо совместной деятельности преподавателя и студента, ведущей к достижению планируемых результатов. В то же время методическое оформление сути технологического процесса придает технологии гибкость и определяется, в частности, как содержанием учебной информации, так и педагогическим мастерством преподавателя. Наиболее адекватной формой и средством развертывания дидактических процессов фундирования и наглядного моделирования является структура дидактического модуля. Дидактический модуль, являясь целостной структурой совместной деятельности учителя и ученика в процессе решения педагогических задач, может быть исследован также как компонент педагогической системы деятельности и, более того, психологической системы деятельности ученика. С точки зрения деятельностной теории учения дидактический модуль должен также содержать ориентировочную, исполнительскую и контрольно-коррекционную части. Это определяет три основных компонента дидактического модуля (ДМ):
-
ориентировочную основу деятельности (как учителя, так и ученика);
-
информационную основу деятельности (как учителя, так и ученика);
-
блок управления учителем когнитивной деятельностью ученика.
Например, первый блок содержит:
-
введение (описание структуры и состава деятельности, особенности учебного предмета);
-
базу данных и базу знаний, необходимых для усвоения нового материала (преемственность деятельности);
-
аннотированную учебную программу, детализированную по уровням усвоения знаний, ступеням абстракции, мотивации и продуктивности учебной деятельности (развернутость содержания);
-
локальные фрагменты (и их динамику) пластов спиралей фундирования, содержащие школьный (профессионально-направленный) и мотивационный компонент (обобщенность деятельности);
-
интегративную экзаменационную программу (интегративные ЗУНМА, творческие задания, общеучебные умения, профессионально-математический базис) как свернутость деятельности и условие для преемственности ДМ.
Требования к проектированию дидактического модуля включают в себя: преемственность содержательных линий школьной и вузовской математики; использование современных форм представления знаний (логической, реляционной, семантической, продукционной, фреймовой); развертывание и свертывание спиралей фундирования базовых учебных элементов школьной математики; блоки мотивационно-прикладных задач, оснащающих спирали фундирования, и др. Ниже представлена схема изучения раздела математики в структуре дидактических модулей ( рис. 1).
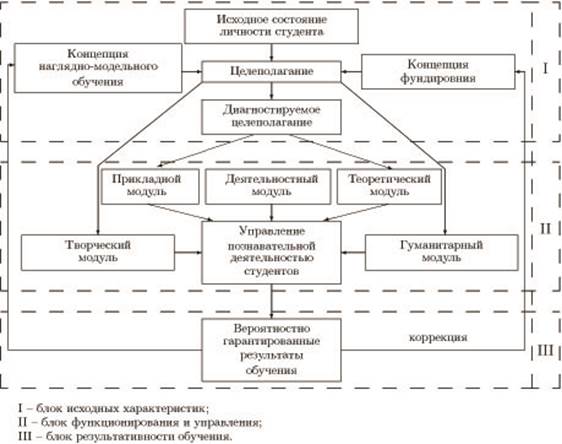
Рис. 1. Схема методики изучения раздела математики (лекция, практическое занятие, тема, дисциплина и т.п.)
Незамкнутость методических параметров обратной связи на блок исходного состояния личности студента означает возможность вариативности методики в зависимости от интеллектуальных и личностных качеств студента. Это означает необходимость создания психологической службы при факультетах с целью мониторинга динамики функционирования личностной сферы каждого студента, а также повышения качества психолого-педагогической подготовки преподавателя с целью профессиональной готовности к психологической дифференциации обучения математике. При этом деятельностный модуль определяет проектирование учебной деятельности студентов, целью и результатами которой является получение конкретных проявлений и конкретизаций математических понятий, утверждений, процедур и алгоритмов, выраженных упорядоченными наборами чисел и простейших геометрических объектов. Определение и наглядное моделирование ориентировочной основы учебной деятельности (ООД) в процессе обучения математике и предъявление ее обучаемому создает положительную мотивацию учения диагностируемого уровня. В основе такого подхода лежит методологический тезис А.Н. Леонтьева: «...актуально сознается только то содержание, которое является предметом целенаправленной деятельности студента, т.е. занимает структурное место непосредственно цели внутреннего или внешнего действия в системе той или иной деятельности» [8]. ООУД представляет собой свернутую структурированную модель ( дидактический модуль) содержания учебной деятельности, адекватно отражающую динамику и логику развертывания учебного содержания (учебных элементов) реального педагогического процесса, включающую таксономию учебных целей и банк спиралей и кластеров фундирования знаний.
Блок исходных характеристик
Процесс обучения математике (например, математическому анализу) предполагает последовательное изучение заранее обусловленных разделов, таких как число, функция, последовательность, предел, производная, интеграл, мера, основные теоремы дифференциального исчисления и т.п. Этот перечень, по существу, дается аннотированной учебной программой (по математическому анализу) и может быть представлен схемой:

причем каждая тема A, B, C,..., X представлена блоком, а ее прохождение – стрелкой. Здесь ¯ означает переход от простого к сложному, от знания неполного к более полному, причем ¯ означает не только логическое строение данного материала, но и превалирующее направление формирования понятий, умений и практических навыков. Однако в процессе преподавания, естественно, приходится устанавливать и проявлять внутренние взаимосвязи между блоками ¯; среди этих взаимосвязей есть существенные, основные, которые, будучи упорядоченными, образуют сквозные связи между блоками, объединенные той или иной сквозной темой, материализацией которых выступают спирали фундирования. Последние же цементируют учебный материал, способствуя дидактическим целям и являясь внешними опорами восприятия обучаемыми сущности рассматриваемых учебных элементов. В то же время выявление и актуализация сквозных тем в качестве существенных внутренних взаимосвязей позволяют активизировать память студентов, варьируя следы предыдущих знаний (остаточные фреймы) в процессе обучения математике. Выделение, систематизация и реализация сквозных тем (а также спиралей фундирования) в курсе математического анализа имеют явную профессионально-педагогическую направленность, поскольку единство математики в реализации внутрипредметных связей выступает прежде всего единой формой теоретического обобщения школьных учебных элементов (предел, производная, непрерывность,...), которая затем конкретизируется, выстраиваясь в дидактически оправданную логическую цепь. Последовательное и настойчивое проведение этой идеи в процессе обучения формирует у будущих учителей важное профессиональное умение – видеть за единой формой базового учебного элемента вузовской математики разнообразное содержание, объединенное единой логической основой. Существенную роль при этом играет адекватное использование информационных технологий и элементов дистанционного обучения [8].
Процесс кодирования базовых учебных элементов приводит к понятию опорной таблицы кодировки (ОТК) [3]. ОТК – это проектирование в форме семантической сети в свернутом виде содержания и структуры базовых учебных элементов учебной дисциплины, которые актуализируются и объективируются в процессе освоения математической деятельности. Состав кодируемых учебных элементов отличается от традиционных ЗУНов (знания, умения, навыки): это ЗУНМА – знания, умения, навыки, математические методы, алгоритмы и процедуры. Каждый компонент ОТК должен быть раскодирован в соответствии с АУП. К основным компонентам, характеризующим состав ориентировочной основы учебной деятельности студента, относятся:
1) базовые знания, умения, навыки, математические методы, процедуры и алгоритмы (ЗУНМА);
2) база данных спиралей и кластеров фундирования, оснащенных мотивационно-прикладными задачами как элементами антиципационной деятельности;
3) аннотированная учебная программа ЗУНМА, конкретизированная:
а) по трем уровням усвоения учебных элементов (по П.Я. Гальперину – Н.Ф. Талызиной);
б) по функциональным компонентам содержания образования (теоретический, практический, прикладной, деятельностный, эвристический, гуманитарный);
4) историко-методическое оснащение базовых учебных элементов, создающее профессиональный контекст в освоении математического знания;
5) основные компоненты, методика и измерители оценочной деятельности;
6) интегративная экзаменационная программа как компонент преемственности дидактических модулей.
Технологические компоненты ДМ
Структура и состав ориентировочной основы учебной деятельности студентов в освоении учебного предмета представлены в следующей последовательности технологических компонентов.
Первый компонент
Базовые знания, умения, навыки, математические методы, алгоритмы и процедуры (для каждого дидактического модуля) — актуализируются в опорной таблице кодировки (ОТК). Свернутое и закодированное содержание обучения в ОТК может развертываться также в четырех сферах:
1) исходные характеристики как когнитивная основа для освоения нового социального опыта в рамках дидактического модуля (ДМ);
2) базовые характеристики как проекция содержания АУП;
3) интегративные характеристики как отражение свернутого результата освоения нового когнитивного опыта в рамках ДМ;
4) дидактические директивы как комплекс правил и предписаний обобщенного характера, определяющих направления и процедуры по достижению учебных целей.
Основная функциональная роль ОТК состоит в содействии формированию устойчивых внутренних опор в ходе освоения учебного содержания (рис. 2).
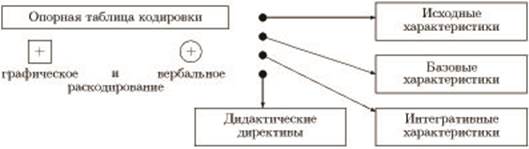
Рис. 2. Технологические конструкты содержания обучения математике
Следующие дидактические правила (директивы) отражают существо технологии наглядного моделирования и сквозные, универсальные, существенные требования к управлению базовыми учебными элементами.
Правило 1. Математическое знание (учебный элемент) должно рассматриваться в динамике взаимопереходов знаковых систем по возможности в четырех сферах: знаково-символической, вербальной, графической и конкретно-деятельностной ( возможна также тактильно-кинестетическая модальность).
Правило 2. Математическое знание (учебный элемент) должно проявляться в ходе освоения учебной деятельности не менее чем в 10 конкретизациях (5 качественных) как частных проявлениях общего.
Правило 3. Освоение существа математического знания (учебного элемента) предполагает осуществление процедуры логического анализа содержания и формы учебного элемента в составе: логическая запись формулировки теоремы или определения понятия, формулировки обратной и противоположной теоремы или конструирование отрицания определения понятия, метод доказательства, блок-схема доказательства, контрпримеры к условиям теоремы с графическими иллюстрациями и т.п.
Правило 4. Мотивационная сфера личности в ходе освоения математического знания (учебного элемента) должна быть актуализирована рассмотрением 2–3 модельно-прикладных задач (в том числе при освоении спиралей и кластеров фундирования знаний).
Правило 5. Математическое знание (учебный элемент) должно проявляться как часть более общего целого знания, в котором оно имеет свои особенности, ограничения и форму.
Правило 6. Математическое знание (учебный элемент) должно рассматриваться в генезисе своего становления, во взаимосвязи с историческим аспектом формы и содержания.
Правило 7. Математическое знание (учебный элемент) должно иметь форму представления посредством простейших количественных и пространственных форм, например в виде числа (действительного или комплексного), геометрической фигуры.
Второй компонент
База данных спиралей фундирования, оснащенных мотивационно-прикладными задачами (СФ). Компонентный состав и структура спирали фундирования базового учебного элемента представлены во фреймовой форме на следующем рисунке 3.
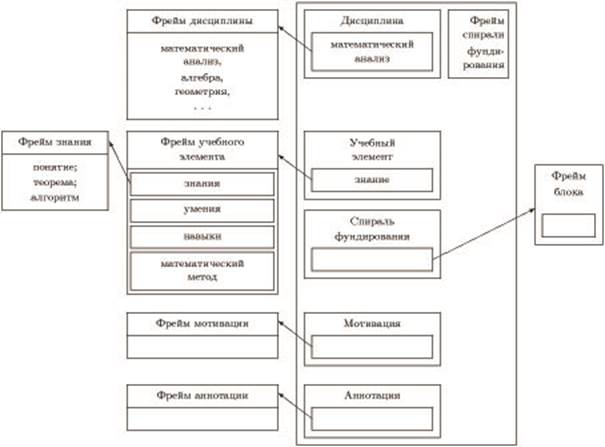
Рис. 3. Фрейм представления теоретического обобщения школьного знания (спираль фундирования)
Третий компонент
Аннотированная учебная программа (АУП) и ее структура представлена на рисунках 4 и 5.
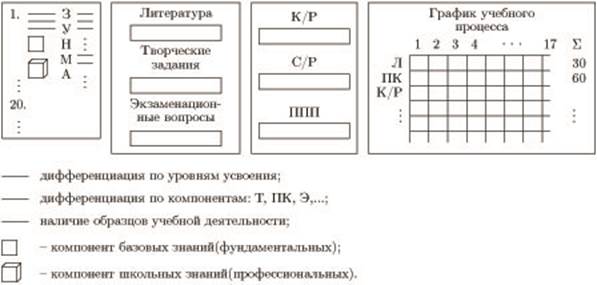
Рис. 4. Компонентный состав АУП с графиком учебного процесса
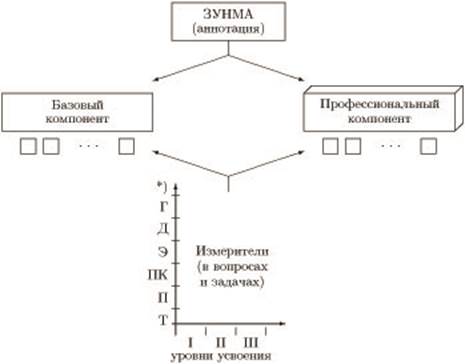
Рис. 5. Детализация компонентов АУП: *) теоретический (Т), прикладной (П), практический (ПК), эвристический (Э), деятельностный (Д), гуманитарный (Г)
Четвертый компонент
Интегративная экзаменационная программа (ИЭП). Общая схема структурирования интегративных учебных элементов из аннотированной учебной программы показана ниже. Реализация целей и задач учебной деятельности студентов всецело определяется требованиями к средствам управления их познавательной деятельностью: методическими приемами, дидактическими правилами, образцами деятельности, материальными и информационными ресурсами. Например, приемы локального моделирования включают: оперативную наглядность, кодирование знаково-символических средств, определение мотивационных блоков, построение семантических и реляционных сетей, структурных блок-схем, логический анализ теорем и структурный анализ понятий. Технология конструирования интегративных учебных элементов представлена на рисунке 6.
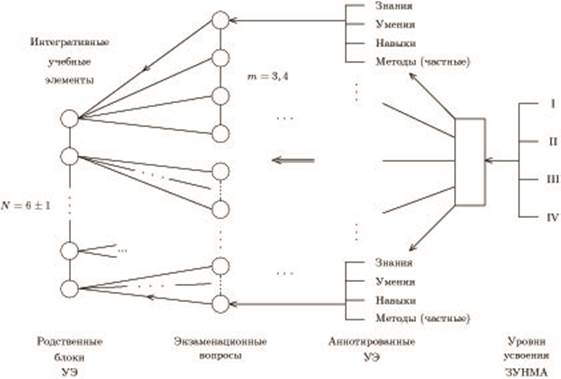
Рис. 6. Технология конструирования интегративных учебных элементов
Требования преемственности ДМ в ходе реализации учебного процесса представлены на рисунке 7.
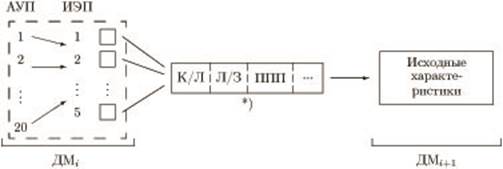
*) К/Л – коллоквиум, Л/З – лабораторные занятия, ППП – педагогические программные продукты,..., ДМ – дидактический модуль
Рис. 7. Требования преемственности ДМ в ходе реализации учебного процесса
Пятый компонент
Историко-методическое оснащение (ИМО) базовых учебных элементов (БУЭ), включающее такие формы, как рефераты, самостоятельные работы, учебно-исследовательские задачи, работа в малых группах, профессиональные пробы, историко-математические экскурсы и иное, осваивается в расчете 1 ч ИМО на 10 ч аудиторных занятий. При этом проектирование элементов базируется на следующих позициях.
Требования:
1) элементы историзма и генезиса УЭ;
2) отбор базовых и интегративных УЭ;
3) взаимопереходы знаковых систем;
4) решение задач при ограничении условий (поиск оптимальных условий);
5) вариативность способов решения задач;
6) структурный анализ УЭ;
7) единичное и особенное проявлений теорий учения в моделировании процессов
усвоения УЭ;
8) актуализация фаз и типов ориентировки и исполнения в учебной деятельности;
9) формирование культуры устной и письменной речи, мышления;
10) фундирование опыта и личностных характеристик в направлении профессионализации;
11) опора на устойчивые ассоциации, активизация ментальных и личностных характеристик.
Основные ЗУНМА являются объектом для целостного изучения наглядным моделированием (структурный анализ, сущность и явление, спирали фундирования, уровни усвоения, историко-методическое оснащение) в составе теоретического, практического, прикладного, мотивационного, деятельностного и эвристического компонентов [9-10]. При этом в соответствии с критерием полноты и оптимальности базовые ЗУНМА школьной математики становятся основным исходным звеном содержания учебных элементов профессионального блока ( I–III семестры). Базовые ЗУНМА вузовской математики проектируются с возможностью логического расширения базового блока до полного объема учебных предметов и покрытия базового блока школьной математики.
Заключение
Реализация инновационной образовательной программы по проектированию содержания инновационных образовательных стандартов высшего педагогического образования на единой основополагающей идеологии фундирования опыта личности не только поднимет на новый уровень содержание и структуру профессиональной подготовки педагога, создаст новое качество профессиональных компетентностей будущего учителя (причем вне зависимости от направления подготовки или специальности обучения), обеспечивающих его конкурентоспособность на рынке труда, укрепит состояние материально-технической базы университета и наукоемкость его лабораторного комплекса, создаст новое учебно-методическое обеспечение учебного процесса, но и создаст прецедент проектирования регионального центра, объединяющего школы, средние профессиональные учебные заведения и университет, оказывающий прямое воздействие на совершенствование образовательной, научной и культурной среды региона.
Рецензенты:
Афанасьев В.В., д.п.н., профессор, ректор Ярославского государственного педагогического университета им. К.Д. Ушинского, г. Ярославль;
Секованов В.С., д.п.н., профессор, заведующий кафедрой информатики Костромского государственного университета им. Н.А. Некрасова, г. Кострома.



