Металлургическое предприятие с точки зрения анализа протекающих в нем процессов представляет собой сложную организационно-техническую систему, состоящую из большого числа разнородных, взаимозависимых элементов, среди которых исследователи выделяют в отдельный класс группу лиц, принимающих решения. Решение логистических или организационных задач в подобных системах невозможно без применения компьютерной поддержки, при этом имитационное моделирование становится наиболее эффективным способом изучения поведения и существенных свойств системы. Применение методов эволюционного моделирования к изучению свойств и поведения сложных систем позволяет использовать естественные законы развития подобных систем для решения оптимизационных задач с помощью генерации и оценки альтернативных вариантов функционирования систем.
Эволюционное моделирование (ЭМ) – хорошо известная и эффективная оптимизационная методология, которую применяют для решения различных задач в науке и технике. Она основана на аналогии с естественными процессами селекции, генетическими преобразованиями и воспроизведением потомства, протекающими в природе. В нашей стране методология ЭМ применительно к решению оптимизационных задач, возникающих в сложных организационно-технических системах, активно развивается научной школой Курейчика В.В. [5; 6]. В популярных системах имитационного моделирования (AnyLogic, Simio, Arena) оптимизация моделируемых процессов осуществляется за счет использования оптимизатора OptQuest, реализующего, в том числе, методы эволюционного моделирования [7]. Существенным ограничением возможностей работы оптимизатора OptQuest на «тяжелых» моделях является этап загрузки данных и генерации первичной структуры модели, сопряженный со значительными временными затратами на каждой итерации и, как следствие, снижением скорости перебора вариантов. Вариантом решения этой проблемы может быть реализация «пользовательского» (нестандартного) эксперимента средствами используемого в системе моделирования ЯВУ (например, Java, C#). Применение подобного варианта сопряжено с требованиями по наличию навыков программирования у аналитика, оптимизирующего производственные процессы. Кроме того, к недостаткам оптимизатора OptQuest можно отнести непрозрачность работы оптимизатора: отсутствие выбора метода оптимизации и настройки параметров работы метода.
Актуальной является разработка гибридного эволюционно-имитационного алгоритма оптимизации процессов и его реализация в модуле оптимизации процессов предприятия (ОПП) автоматизированной информационной системы моделирования производственных процессов (АИС МОД). АИС МОД является подсистемой системы выпуска металлургической продукции (АС ВМП), представляющей собой web-ориентированную систему, предназначенную для слежения, контроля, моделирования, анализа и совершенствования процессов выпуска металлургической продукции [1; 8; 9].
Реализация эволюционно-имитационного алгоритма
Эволюционно-имитационный алгоритм, реализуемый в модуле ОПП АИС МОД, основан на методе мультиагентной генетической оптимизации, подробно описанном в работах [2; 3]. Рассмотрим этапы реализации алгоритма в модуле ОПП.
Этап 1. Выбор способа кодирования оцениваемого альтернативного решения задачи в особь-хромосому. Под особью (хромосомой) будем понимать строку символов, кодирующую некоторое решение оптимизационной задачи. Под решением оптимизационной задачи (не обязательно оптимальным, но допустимым) понимается набор значений M входных управляемых параметров системы. Данные значения согласно некоторому правилу (способу кодирования) должны быть закодированы в строку символов – особь (хромосому). Отдельный символ хромосомы называется геном (всего ген в хромосоме Q). Число N хромосом образуют популяцию хромосом (популяцию особей). Методы ЭМ работают с популяцией особей и с каждым шагом изменяют ее с целью нахождения лучшей особи. Пригодность (оптимальность) особи оценивается ее функцией пригодности (ФП). ФП рассчитывается для каждой особи исходя из оценки с помощью имитационной модели последствий реализации решения, закодированного в рассматриваемой особи.
Рассмотрим реализуемый способ декодирования хромосом. Введем следующие индексы: 
. Будем использовать следующие обозначения: Di=[ai;bi] – диапазон изменения значения управляемого параметра Pi; Δi=0-ai – смещение диапазона значений параметра Pi; Di’=[ai+Δi;bi+Δi] – нормированный диапазон изменения значения управляемого параметра Pi; qi - количество ген, необходимое для двоичной записи верхней границы нормированного диапазона Di’ изменения значения управляемого параметра Pi: ∑ qi=Q. Пусть текущая популяция состоит из N строк, заполненных 0 и 1: 
. Рассмотрим реализуемый алгоритм декодирования набора строк S в набор управляемых параметров P={Pi,k}.
a. k=1
b. Разбиение строки Sk на M подстрок размером qi каждая 
, где
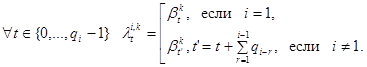
c. Декодирование каждой подстроки 
строки 
в значение параметра 
:
.
d. Преобразование параметров в параметры 
по формуле:
.
e. Проверка выполнения условия ai≤Pi≤bi для всех i. Если условие выполнено, то переход на шаг g. Если условие не выполнено для некоторых i, то формирование случайным образом новой строки , переход на шаг b.
f. Если k<N, то k=k+1 и переход на шаг b, иначе переход на шаг g.
g. Конец декодирования.
Этап 2. Разработка операторов изменений особей-хромосом (генетических операторов). В результате работы генетических операторов меняется символьная строка, кодирующая решение, следовательно, меняется и решение задачи, представленной данной строкой. Применение генетических операторов к текущей популяции особей позволяет получить новую популяцию особей. Декодирование особей новой популяции приводит к формированию набора новых решений поставленной задачи. В качестве генетических операторов были использованы стандартные операторы: оператор кроссинговера, оператор мутации и оператор инверсии [6]. Для каждого оператора предполагается задание пользователем вероятности его применения.
Этап 3. Определение законов выживания решения (законов селекции или отбора решений-хромосом в следующую популяцию). В качестве закона отбора решения в следующую популяцию был реализован закон рулетки [6]. Согласно данному закону каждому решению ставится в соответствие вероятность его отбора, связанная с ФП решения (чем выше ФП, тем выше вероятность отбора решения).
Этап 4. Выбор способа генерации начальной популяции и способа останова работы алгоритма. Генерация начальной популяции реализована случайным образом. Способ останова алгоритма выбран по достижению заданного пользователем числа популяций.
Этап 5. Реализация лежащего в основе гибридного алгоритма метода мультиагентной генетической оптимизации на языке Java.
Этап 6. Реализация интерфейса взаимодействия пользователя с эволюционно-имитационным алгоритмом.
Пользователь в ходе взаимодействия с эволюционно-имитационным алгоритмом задает: параметры работы алгоритма (число хромосом в популяции, число популяций как признак останова работы алгоритма, вероятности применения генетических операторов мутации и инверсии), входные параметры имитационной модели и диапазоны их изменения, выходной параметр имитационной модели для расчета ФП решений, длительность моделирования (количество тактов модельного времени).
Отладка эволюционно-имитационного алгоритма
Рассмотрим отладку реализованного гибридного эволюционно-имитационного алгоритма на примере решения задачи оптимизации логистических процессов выпуска металлургической продукции (ВМП). Рассматриваемые процессы связаны с движением единиц продукции (ЕП) по агрегатам конвертерного и прокатного производства и дальнейшей погрузкой ЕП со склада готовой продукции в подвижной состав, приходящий раз в сутки. Детальная постановка задачи приведена в [4]. Необходимо определить оптимальное соотношение количества вагонов подвижного состава и интенсивности генерации заявок на производство ЕП с целью минимизации среднего времени простоя поданных вагонов T перед погрузкой и минимизации объема склада готовой продукции V. Количество вагонов меняется в пределах от 4 до 20 штук; интенсивность генерации заказов на производство меняется в диапазоне от 1 мин до 15 мин с шагом 1 мин. Время моделирования – 3000 минут. Для решения данной задачи в модуле создания моделей процессов (СМП) АИС МОД была разработана имитационная модель процессов ВМП, описание которой приведено в [4]. Данная модель была модифицирована с целью расчета на выходе модели характеристик T и V. В результате был описан выходной параметр «Выход модели» Out, рассчитываемый следующим образом (с учетом максимизации данного ресурса): Out=Round(1000000/(T+10∙V)). Структура модели приведена на рис. 1.
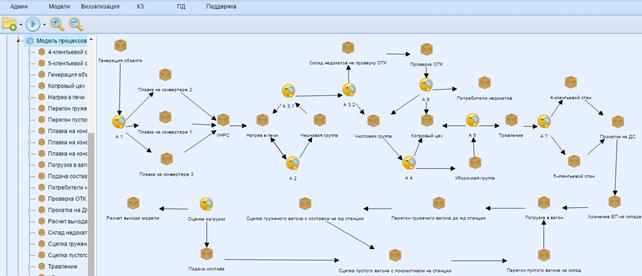
Рис. 1. Структура имитационной модели процессов ВМП в модуле СМП АИС МОД.
В результате работы эволюционно-имитационного алгоритма было получено следующее решение: для минимизации среднего времени простоя поданных вагонов T перед погрузкой и минимизации объема склада готовой продукции V необходимо обеспечить интенсивность генерации заказов на производство с периодичностью раз в 15 минут и количество вагонов подвижного состава в количестве 14 штук. Данное решение соответствует следующим значениям выходных характеристик решаемой задачи: Т=699 мин, V=10 шт. Информация, введенная пользователем для работы эволюционно-имитационного алгоритма, и результат работы алгоритма, формируемый модулем ОПП АИС МОД, представлены на рис. 2.
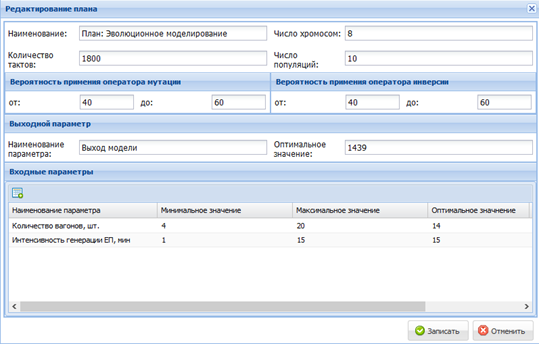
Рис. 2. Интерфейс эволюционно-имитационного алгоритма в модуле ОПП АИС МОД.
По окончании работы эволюционно-имитационного алгоритма был сформирован файл с расширением .xlsx, содержащий подробную информацию о ходе решения оптимизационной задачи. На основании анализа данного файла были построены зависимости максимального, минимального и среднего значений ФП хромосом от номера популяции, представленные на рис. 3. Как следует из рисунка, с ростом номера популяции среднее значение ФП имеет тенденцию к возрастанию, максимальное значение ФП возрастает незначительно, а минимальное значение ФП подвержено сильным колебаниям. Последнее обстоятельство обеспечивает каждую новую популяцию генетическим разнообразием для поиска новых решений и выхода из локального оптимума.
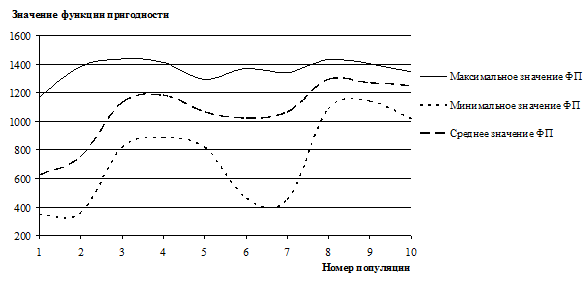
Рис. 3. Зависимость значений ФП от номера популяции в ходе решения задачи.
Работа эволюционно-имитационного алгоритма была проанализирована при смене числа хромосом в популяции и смене числа поколений (предельного числа популяций). Была проанализирована зависимость процента решений, не удовлетворяющих ограничению на принадлежность управляемого параметра Pi решения диапазону Di изменения значений данного параметра (рис. 4, левый график). Также была проанализирована зависимость процента решений с высокой ФП, т.е. с ФП, отличной от найденной максимальной ФП не более чем на 5% (рис. 4, правый график).
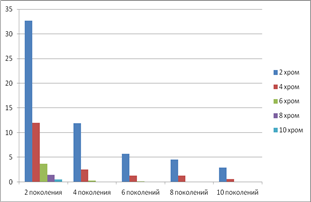
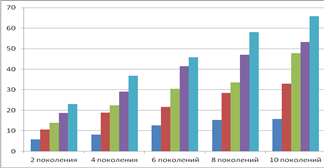
Рис. 4. Зависимость процента не удовлетворяющих ограничениям решений (слева) и процента решений с высокой ФП (справа) от числа поколений и числа хромосом в поколении.
Как следует из анализа графиков, приведенных на рис. 4, увеличение числа поколений снижает процент не удовлетворяющих ограничениям решений, что связано с закреплением в каждом последующем поколении удовлетворяющих ограничениям решений. Зависимость процента не удовлетворяющих ограничениям решений от роста числа хромосом в поколении незначительна при применении числа хромосом не менее 6. Одновременное увеличение числа поколений и числа хромосом в поколениях повышает процент решений с высокой ФП, что связано с повышением разнообразия генетического материала.
Таким образом, можно рекомендовать пользователю следующие настройки работы эволюционно-имитационного алгоритма: применение числа хромосом в поколении в размере не менее 6 хромосом и задание останова работы алгоритма при смене 10 поколений.
Заключение
В ходе работы была решена задача реализации эволюционно-имитационного алгоритма оптимизации процессов в модуле ОПП системы моделирования производственных процессов металлургического предприятия АИС МОД АС ВМП. В указанном алгоритме реализован разработанный ранее метод мультиагентной генетической оптимизации.
Проведено тестирование гибридного алгоритма на примере решения задачи оптимизации логистических процессов выпуска металлургической продукции. Для данной задачи получено следующее решение: интенсивность генерации заказов на производство – каждые 15 минут, количество вагонов подвижного состава – 14 штук. Проведена отладка работы алгоритма с целью настройки следующих параметров его работы: числа популяций и числа хромосом в популяции. По результатам тестирования выявлены рекомендации по настройке пользователем параметров эволюционно-имитационного алгоритма.
Работа выполнена в рамках договора № 02.G25.31.0055 (проект 2012-218-03-167) при финансовой поддержке работ Министерством образования и науки Российской Федерации.
Рецензенты:
Доросинский Л.Г., д.т.н., профессор, заведующий кафедрой теоретических основ радиотехники, ФГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург;
Поршнев С.В., д.т.н., профессор, заведующий кафедрой радиоэлектроники информационных систем, ФГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург.