Цель исследования: модернизация средств и методик проведения учебного вычислительного эксперимента в практике преподавания естественнонаучных и инженерных дисциплин, на примере совершенствования методики проведения электротехнического вычислительного эксперимента при исследовании переходного процесса в линейной электрической цепи методом интеграла Дюамеля.
Материал и методы исследования: моделирование процесса обучения на основе использования современных компьютерных технологий, математическое моделирование, обобщение опыта.
Результаты исследования и их обсуждение. Исследование переходного процесса, возникающего в ЛЭЦ в ответ на входное импульсное воздействие сложной формы (отклика электрической цепи на импульсное воздействие сложной формы) – задача трудоемкая. В качестве основных программных продуктов для ее решения мы исследовали пакеты компьютерной математики SCILAB и WOLFRAM MATHEMATICA.
Пакет компьютерной алгебры WOLFRAM MATHEMATICA предоставляет пользователю достаточно широкие возможности для расчета переходных процессов. Впрочем, данный пакет применяется российскими студентами и курсантами достаточно ограниченно: во-первых, он дорог, во-вторых, есть достойные бесплатные альтернативы (в частности, пакет компьютерной математики SCILAB). Однако в некоторых задачах, например, при вычислении интеграла Дюамеля, пакет WOLFRAM MATHEMATICA более удобен.
Сегодня появилась бесплатная онлайн-версия этого продукта: WOLFRAM Mathematica Online. Исполнительный директор фирмы Wolfram, Стивен Вольфрам, сообщил, что почти все особенности компьютерных приложений доступны в этой браузерной версии пакета.
Наше исследование доказало справедливость этого утверждения. Мы рассмотрели возможности версии WOLFRAM Mathematica Online, при выполнении вычислительного эксперимента по исследованию переходного процесса в линейной электрической цепи методом интеграла Дюамеля.
На рис. 1 приведены: (a) – схема исследуемой цепи; (b) – график изменения ЭДС источника импульсного сигнала, действующего на входе исследуемой цепи. Параметры элементов цепи известны: R1 = R3 = 100 Ом; L = 0,35 Гн; C = 30 мкФ; R2 = R4 = 20 Ом;
|
Проиллюстрируем возможности WOLFRAM Mathematica Online при расчете отклика тока конденсатора, включенного в ветвь ЛЭЦ, в ответ на входное импульсное воздействие сложной формы. Расчет переходной проводимости операторным методом. Операторная схема замещения |
Рис. 1. Схема исследуемой цепи (a), |
Для составления операторной схемы замещения исследуемой ЛЭЦ катушку и конденсатор исходной цепи заменяем их операторными изображениями для нулевых начальных условий, рис. 2. Катушку заменили операторным сопротивлением Lp, конденсатор – операторным сопротивлением 1/Cp.
|
Примем величину ЭДС источника входного питания равной 1 В, его операторное изображение E0/p = 1/p В этом случае оригинал операторного изображения тока ветви с конденсатором будет равен переходной проводимости. |
Рис. 2. Операторная схема замещения |
На операторной схеме система контуров выбрана таким образом, чтобы при расчете операторного тока конденсатора методом контурных токов, достаточно было найти лишь ток первого контура I11(p), равный искомому IC(p).
Операторное изображение тока конденсатора. Для расчета операторного тока конденсатора IC(p) методом контурных токов, составим систему контурных уравнений.
Все элементы полученной нами системы контурных токов являются операторными изображениями сопротивлений токов и ЭДС. Матричное уравнение, описывающее исследуемую цепь в соответствии с методом контурных токов, имеет следующий вид:
![]() ,
,
где ![]() – матрица контурных сопротивлений, ее
коэффициенты:
– матрица контурных сопротивлений, ее
коэффициенты:
Z11 = R2 + R4 + 1/Cp; Z22 = R1 + R3 + R4 + Lp; Z33 = R1 + R2 + Lp;
Z12 = Z21 = R4; Z13 = Z31
= – R2; Z23 = Z32 = R1 + Lp;
![]() – матрица операторных изображений контурных
токов, ее элементы нам неизвестны.
– матрица операторных изображений контурных
токов, ее элементы нам неизвестны.
Первый
элемент этой матрицы – операторное изображение
тока первого контура мы должны найти; ![]() –
матрица операторных изображений контурных ЭДС, ее коэффициенты:
–
матрица операторных изображений контурных ЭДС, ее коэффициенты:
E11 = 0; E22 = E33 = E/p = 1/p.
Используя пакет WOLFRAM Mathematica Online, решим это матричное уравнение. Студентам мы рекомендуем обращаться за консультацией к иллюстрированному самоучителю по работе с пакетом Wolfram Mathematica, Интернет-адрес ресурса [1].
Для решения задачи выходим на Интернет-страницу WOLFRAM Mathematica Online, Интернет-адрес ресурса [6]. Кликнув в панели входа в аккаунт кнопку «Create Account», регистрируемся и создаем личный аккаунт. Входим в свой аккаунт. Открыв ячейку ввода в окне блокнота, введем программный код для решения нашей задачи, рис. 3.
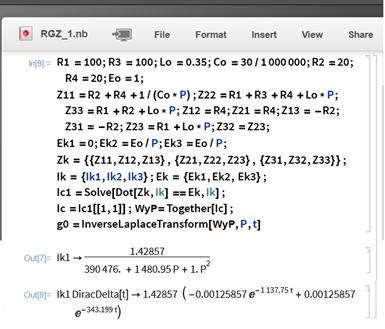
Рис. 3
Следует обратить внимание на то, что многие заглавные символы алфавита зарезервированы пакетом Wolfram Mathematica в качестве служебных. Например, I – этим символом обозначается мнимая единица, E – основание натурального логарифма, и т.д. Поэтому мы усложняли символьные обозначения, например, ЭДС – Eo, индуктивность – Lo.
Для
запуска командного кода на исполнение нажимаем клавишу «Enter» на цифровой клавиатуре или комбинацию клавиш «Shift + Enter» на основной
клавиатуре. На рис. 3,
в ячейках вывода, показан результат исполнения командного кода. Таким образом, передаточная функция по
проводимости имеет вид:
![]() ,
,
Соответственно, переходная проводимость цепи
![]()
Чтобы раскрыть скобки полученного выражения дополним программный код командой Expand[g0]. После исполнения модифицированного кода получим выражение для переходной проводимости цепи:
g(t) = – 0,00179796 e–1137,75 t + 0,00179796 e–343,199 t;
Расчет отклика тока ветви с конденсатором методом интеграла Дюамеля
· на третьем участке входной импульс делает скачок на 100 В, а затем линейно снижается с 200 до 100 В;
· на четвертом участке входной импульс скачком падает от 100 В до 0, чем входной импульс и завершается;
· продолжительность по времени каждого из трех первых участков τmax = 3 мс = 0,003 с.
Интеграл Дюамеля и отклик тока конденсатора на первом участке. Для первого участка интеграл Дюамеля для вычисления отклика тока в ветви с конденсатором имеет вид:
iI(t) = ∆uI g(t) + 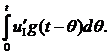
В этом уравнении ∆uI – скачок напряжения входного сигнала на первом участке,
∆uI = 100 В,
а u' – скорость изменения входного сигнала на этом участке:
uI' = ∆uI/τmax = – 100/0,003 ≈ – 33333,3 В/с.
Рассчитаем интеграл Дюамеля для первого участка в среде пакета WOLFRAM Mathematica Online. Запишем программный код решения этой задачи.
- Откроем в блокноте своего аккаунта новую ячейку ввода. Объявим значения коэффициентов, характеризующих воздействующий сигнал на первом участке (du1 – скачок входного сигнала в начале участка, tau – правая временная граница участка, k1 - угловой коэффициент прямой графика для первого участка):
du1=100;tau=0.003;k1=-du1/tau;
- Далее следует уравнение переходной проводимости gt:
gt=-0.00179796*E^(-1137.75*t)+0.00179796*E^(-343.199*t);
- Запишем уравнение переходной проводимости gθ в виде, необходимом для интегрирования по промежуточной переменной θ:
gθ=-0.00179796*E^(-1137.75*(t-θ))+0.00179796*E^(-343.199*(t-θ));
- Запишем код для вычисления отклика тока с помощью интеграла Дюамеля:
iC1=du1*gt+k1*Integrate[gθ,{ θ,0,t}];
- Оптимизируем выражение отклика тока. С помощью команды Together мы запускаем подпрограмму приведения выражения к общему знаменателю. Команда Expand обеспечивает раскрытие скобок.
iC01=Expand[Together[iC1]]
- Переменной IntervaL1 присваиваем программный код вывода графика отклика тока на первом участке: командой Plot выводим график функции iC01 в диапазоне изменения времени t от 0 до tau:
IntervaL1=Plot[iC01,{t,0,tau},GridLines -> Automatic, Frame -> True]
Параметры GridLines -> Automatic, Frame -> True обеспечивают вывод координатной сетки и автоматический выбор размеров графического окна.
Запустив режим исчисления, получили отклик тока конденсатора на первом участке:
iI(t) = – 0,121952 – 0,232472 e–1137,75t + 0,354424 e–343,199t.
Интеграл Дюамеля и отклик тока конденсатора на втором, третьем и четвертом участках рассчитываем аналогично. Для второго участка интеграл Дюамеля для вычисления отклика тока в ветви с конденсатором имеет вид:
iII (t) = ∆uI g(t) + 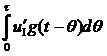 + ∆uII g(t – τ) +
+ ∆uII g(t – τ) + 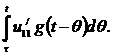
Запустив режим исчисления, получили отклик тока конденсатора на втором участке:
iII (t) = – 4,09232 e–1137,75t + 0,368895 e–343,199t.
Программный код решения этой задачи в среде пакета WOLFRAM Mathematica Online создается аналогично коду, который мы разрабатывали для первого участка.
Для создания этого кода мы открыли в блокноте новую ячейку ввода и скопировали в нее содержимое предыдущей ячейки – код для расчета отклика тока на 1-м участке. Далее мы модифицировали этот код:
- изменили номер участка в ремарках;
- дописали в исходные данные «du2=100;» – значение величины скачка напряжения в начале второго участка;
- поменяли обозначение gt1 на gt2, а в выражении для gt2 мы время t заменили на выражение (t - tau);
- поменяли обозначение iC1 на iC2, а в выражении для iC2 мы заменили верхний предел интегрирования: вместо переменной t мы поставили числовую границу tau. Кроме этого, мы дополнили iC2 откликом на скачок напряжения du2*gt2.
Выражение, полученное для отклика тока конденсатора на третьем участке, имеет вид:
iIII (t) = – 0,121952 – 218,422 e–1137,75t + 3,14745 e–343,199t.
Выражение, полученное для отклика тока конденсатора на четвертом участке, имеет вид:
iIV (t) = 6289,43 e–1137,75t – 4,63233e–343,199t.
Последняя строка кода склеивает графики всех четырех участков:
Show[IntervaL1,IntervaL2,IntervaL3,IntervaL4,PlotRange-> Automatic]
На рис. 5 приведен график отклика тока конденсатора, полученный после исполнения последней строки программного кода.
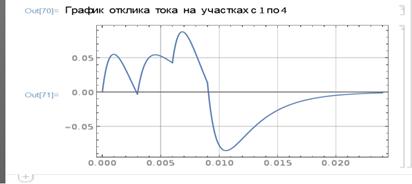
Рис. 5. График отклика тока конденсатора
Заключение
Использование Интернет-ресурса WOLFRAM Mathematica Online в учебном вычислительном эксперименте естественнонаучных и инженерных дисциплин целесообразно по ряду соображений.
Потенциал предметного содержания естественнонаучных и инженерных дисциплин может быть реализован, при условии активной познавательной деятельности курсантов и студентов по освоению изучаемой дисциплины.
Продуктивное усвоение студентами и курсантами предметного материала дисциплины на основе учебного вычислительного эксперимента определяет мотивационный аспект, формирует познавательный интерес и ценностное отношение к профессиональным знаниям.
Наряду с мотивационным аспектом, практико-ориентированное обучение естественнонаучным и инженерным дисциплинам обеспечивает инженерному образованию содержательный и процессуальный аспекты, способствует повышению уровня физического осмысления процессов, протекающих в изучаемых технических устройствах. Практико-ориентированное обучение позволяет достичь более глубокого усвоения знаний, необходимых для профессиональной деятельности инженера, приобрести умение прогнозировать явления, происходящие в изучаемых технических объектах, учит основам конструирования новых технических устройств с заданными функциональными свойствами.
Рецензенты:
Власов А.Б., д.т.н., профессор, Заместитель начальника по научной работе Морской академии Мурманского государственного технического университета, г. Мурманск;
Морозов Н.Н., д.т.н., профессор, заведующий кафедрой общей и прикладной физики Мурманского государственного технического университета, г. Мурманск.




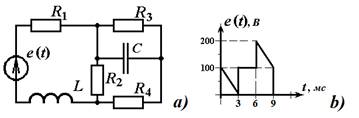
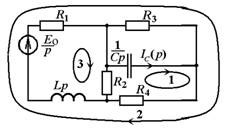
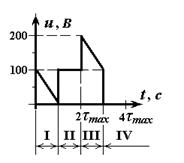 Рис.
4
Рис.
4