В связи с увеличивающимися потребностями современного производства возникает необходимость в использовании новых конструкционных материалов. Одними из перспективных материалов, исследуемых в настоящее время, являются армированные пластики. Они представляют собой композиционный материал, состоящий из матрицы со включенными в нее армирующими элементами. В качестве матрицы используют термореактивные и термопластичные полимеры, синтетические смолы, например эпоксидные и полиэфирные смолы. Армирующим наполнителем служат синтетические, органические и неорганические волокнистые материалы. В зависимости от наполнителя армированные пластики делят на стеклопластики (стекловолокно), углепластики (углеволокно), боропластики (борное волокно), асбопластики (асбестовое волокно) и др. Армированные пластики применяются в автомобильной, аэрокосмической промышленности, самолетостроении и других областях промышленности. Свойства армированных пластиков, такие как малая плотность и высокая прочность, дают им преимущества перед традиционными материалами. Разработаны различные добавки, позволяющие изменять свойства пластмасс, например, такие как теплопроводность. У стандартных пластмасс теплопроводность находится в районе 0,1–0,3 Вт/(м K), но были разработаны теплорассеивающие пластмассы с теплопроводностью до 40 Вт/(м K).
Производство изделий из армированных пластмасс требует механической обработки для получения точных размеров и высокого качества поверхности. Основным видом механической обработки пластмасс является фрезерование. Неоднородность армированных пластмасс является существенной проблемой для механической обработки. При выборе режущего инструмента особое внимание стоит обратить на армирующие волокна. Параметры обработки зависят не только от материала армирующего наполнителя, но и от его расположения. Некорректно выбранные режимы фрезерования могут привести к расслоению, сколам, оплавлению, прилипанию стружки к фрезерному инструменту и обработанной поверхности, вырывам и другим дефектам обработки. Поэтому разработка математических моделей механической обработки армированных пластмасс является актуальной задачей.
Определим взаимосвязи параметров фрезерования армированных пластмасс с помощью анализа размерностей. Для описания состояния механической системы выведем уравнения движения и найдем величины, входящие в эти уравнения. Определим совокупность параметров, однозначно характеризующих процесс фрезерования пластмасс. С помощью анализа размерностей найдем безразмерные комплексы. В качестве основных единиц примем измерения времени T [с], массы M [кг] и длины L [м] согласно международной системе единиц (СИ).
Скорость резания V и подача S фрезы являются основными факторами, определяющими процесс фрезерования. Еще одним важным параметром фрезерования является тангенциальная сила резания F (рис. 1). Нерегламентированные значения сил резания могут привести к повреждениям обрабатываемой поверхности. Поэтому прогнозирование силы резания играет важную роль при выборе параметров фрезерования. Большое значение для качества поверхности оказывает глубина резания t. Основную механическую характеристику обрабатываемого материала представляет предел прочности при растяжении σ.
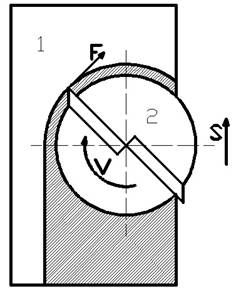
Рис.1. схема фрезерования армированного пластика
1 — обрабатываемый пластик, 2 — фреза
Основной целью данной статьи является получение математической модели процесса фрезерования армированных пластмасс, показывающей влияние скорости резания V и подачи S фрезы и их взаимовлияние на основные параметры процесса фрезерования.
Занесем выбранные параметры, определяющие процесс фрезерования армированных пластмасс, в таблицу с указанием формулы размерности.
Таблица 1
Параметры, характеризующие процесс фрезерования пластмасс и формулы их размерностей
|
Параметры |
Обозначения |
Формула размерности |
|
Скорость резания, м/с |
V |
|
|
Скорость подачи, м/с |
S |
|
|
Глубина резания, м |
t |
|
|
Тангенциальная сила резания, Н |
F |
|
|
Предел прочности при растяжении, МПа |
σ |
|
Представим значение силы резания F как функционал от определяющих параметров, выбранных для описания процесса фрезерования пластмасс:
![]() (1)
(1)
Исходя из π-теоремы подобия, которая позволяет определить общую структуру зависимости, выражение (1) можно выразить через n – k = 5 – 3 = 2 безразмерных степенных комплекса и симплекса, где n — количество физических величин, входящих в уравнение, k — наибольшее число величин с независимыми размерностями. Комплексом называют безразмерную комбинацию размерных величин, симплексом — отношение двух величин, имеющих одинаковые размерности.
Для нахождения чисел подобия с помощью анализа размерностей используем метод Релея [1] для решения размерных систем. Суть метода состоит в том, что искомая величина представляется как степенной комплекс через влияющие на нее параметры. Степенной комплекс включает используемые в анализе величины в различных степенях.
Предположим, существует соотношение:
![]() (2)
(2)
Подставим значения размерностей:
![]() (3)
(3)
Составим систему уравнений для показателей степеней, при выполнении которых уравнение будет однородным по размерностям:
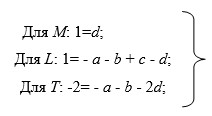
Решая данные уравнения в системе, получим:
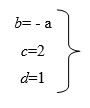
Найденные значения показателей степеней подставим в уравнение (2):
![]() (4)
(4)
или
F/(![]() ·
· ![]() ) = f[
) = f[![]() ] (5)
] (5)
Получим безразмерный комплекс
π1 = F/(![]() ·
· ![]() ) (6)
) (6)
и симплекс
π2 = ![]() (7)
(7)
Для описания процесса фрезерования армированных пластмасс достаточно выявить зависимость между числами подобия π1 = F/(![]() ·
· ![]() ) и π2 =
) и π2 = ![]() .
.
Рассмотрим физический смысл полученных безразмерных комплекса и симплекса. Подача S и скорость резания V, входящие в состав симплекса π2, характеризуют линейную производительность процесса фрезерования в единицу времени и путь резания соответственно. Таким образом, π2 = ![]() – отношение пути резания к линейной производительности процесса – обобщенная характеристика режима фрезерования армированных пластмасс, называемая также числом подобия режима [4].
– отношение пути резания к линейной производительности процесса – обобщенная характеристика режима фрезерования армированных пластмасс, называемая также числом подобия режима [4].
Комплекс π1 = F/(![]() ·
· ![]() ) является отношением действующего в материале напряжения, создаваемого тангенциальной составляющей силы резания, к пределу прочности материала при растяжении. Это соответствует закону Герца для условий контактных деформаций упругих тел [2], подтвержденный экспериментально Ауэрбахом, который показывает, что процесс съема материала происходит при напряжениях в зоне резания, превышающих предел прочности обрабатываемого материала. Следовательно, условие для фрезерования можно записать в виде:
) является отношением действующего в материале напряжения, создаваемого тангенциальной составляющей силы резания, к пределу прочности материала при растяжении. Это соответствует закону Герца для условий контактных деформаций упругих тел [2], подтвержденный экспериментально Ауэрбахом, который показывает, что процесс съема материала происходит при напряжениях в зоне резания, превышающих предел прочности обрабатываемого материала. Следовательно, условие для фрезерования можно записать в виде:
π1 = F/(![]() ·
· ![]() )≥1 (8)
)≥1 (8)
Безразмерный комплекс π1 = F/(![]() ·
· ![]() ) является так называемым критерием съема материала. Этот критерий несет информацию о ходе процесса фрезерования армированных пластмасс.
) является так называемым критерием съема материала. Этот критерий несет информацию о ходе процесса фрезерования армированных пластмасс.
Для упрощения модели F/(![]() ·
· ![]() ) = f[
) = f[![]() ], можно использовать предложенную Ю. Н. Полянчиковым, Е. М. Фроловым и Д. С. Клюйковым методологию построения и анализа регрессионных моделей [3].
], можно использовать предложенную Ю. Н. Полянчиковым, Е. М. Фроловым и Д. С. Клюйковым методологию построения и анализа регрессионных моделей [3].
Коэффициенты уравнения регрессии можно определить по методу наименьших квадратов по следующим формулам:
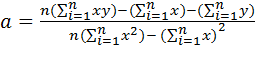 (9)
(9)
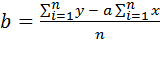 (10)
(10)
где y – значение функции отклика в i-м опыте; x – значение фактора в i-м опыте; n – число опытов.
Главным преимуществом найденной математической модели является то, что она позволяет оценить влияние скорости резания V и подачи S, а также их взаимовлияния на ход процесса фрезерования армированных пластмасс. Математическая модель позволяет выбрать методику проведения экспериментов для подбора оптимальных режимов фрезерования армированных пластмасс.
Рецензенты:
Яковлев А.А., д.т.н., профессор, декан факультета автоматизированных систем и технологической информатики, Волгоградский государственный технический университет, г. Волгоград;
Полянчиков Ю.Н., д.т.н., профессор кафедры «Технология машиностроения», Волгоградский государственный технический университет, г. Волгоград.



