В данной статье под методикой оценки качества предоставления услуг в инфокоммуникационной сети на основе механизмов приоритезации трафика понимается последовательность выполнения расчетов внешних характеристик сети, включающих частные (вспомогательные) и обобщенные (итоговые) показатели качества предоставления заданных услуг, при заданных внутренних характеристиках, определяемых моделью инфокоммуникационной сети, учитывающей механизмы приоритезации трафика, и заданных внешних характеристиках, определяемых моделью условий функционирования, а также сравнение полученных результатов с требуемыми (допустимыми) значениями.
Данная методика оценки может быть использована как контрольный механизм для проверки качества проектируемой или уже спроектированной. Однако сама методика не говорит о том, какие надо задавать параметры технологий, и не дает рекомендаций по перебору с целью поиска лучшего или подходящего варианта построения сети. В то же время с помощью данной методики оценки можно найти параметры технологий инфокоммуникационной сети (ИКС), обеспечивающие выполнение требований к качеству предоставляемых услуг.
Общая структура методики
Под методикой оценки качества предоставления услуг в инфокоммуникационной сети на основе механизмов приоритезации трафика в работе понимается последовательность выполнения расчетов внешних характеристик qрсч, соответствующих моделям потребностей, при заданных внутренних характеристиках mздн, соответствующих модели технологии построения ИКС, и заданных внешних характеристиках Uздн, соответствующих модели условий функционирования, расчета обобщенного показателя эффективности Qрсч(qрсч,qздн), учитывающего отклонения рассчитанных значений qрсч от заданных qздн, а также сравнение полученных результатов с требуемыми (допустимыми) значениями Qздн
Основу методики оценки составляет последовательность математических расчетов промежуточных (вспомогательных) и итоговых показателей качества (ПК) (внутренних и внешних характеристик) в соответствии с причинно-следственной связью моделей процессов функционирования сети, позволяющих учесть влияние на указанные показатели (внешние характеристики) параметров приоритезации (внутренние характеристики).
На рисунке 1 приведена блок-схема методики оценки предоставления услуг в инфокоммуникационной сети на основе механизмов приоритезации трафика.
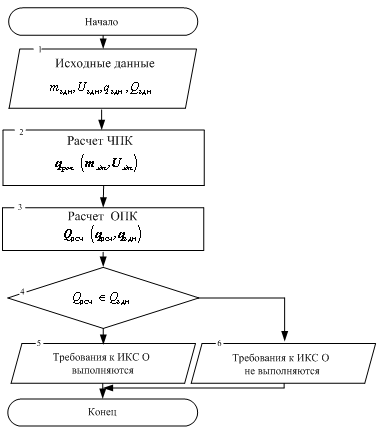
Рис. 1. Блок-схема методики оценки предоставления услуг в инфокоммуникационной сети на основе механизмов приоритезации трафика
В состав исходных данных (блок 1) методики анализа технологий построения ИКС входят заданные (задаваемые) внутренние характеристикиm здн и внешние характеристики Uздн , а также требуемые (допустимые) значения qздн,Qздн
В блоке 3 выполняется расчет обобщенного показателя эффективности Qрсч(qрсч,qздн).
В блоках 4 производится сравнение рассчитанных характеристик ПК Qрсч с заданными (допустимыми) характеристиками Qздн. В случае, если все рассчитываемые характеристики принадлежат области допустимых значений, то в блоке 6 делается вывод о том, что требования к ИКС выполняются, то есть анализируемая технология годится для построения ИКС. В противном случае, если хотя бы одна из характеристик не принадлежит области допустимых значений, то в блоке 7 делается вывод, что требования к ИКС не выполняются, то есть анализируемая технология не годится для построения ИКС.
Частные аспекты специфики объекта исследований рассмотрены при разработке модели ИКС. Однако важно предварительно определиться концептуально (но достаточно конкретно для возможности последующей детализации модели) с общим подходом к постановке и решению задачи.
Примером вполне конструктивного подхода к решению задачи «мультиоптимизации» сетей связи является подход, изложенный в [4]. Данный подход рекомендуется авторами для использования при оптимизации перспективных инфокоммуникационных сетей связи, обслуживающих информационные потоки различной природы, и, следовательно, заслуживает в настоящей работе особого внимания.
Информационный обмен между уровнями формируется в соответствии с принципом минимаксного построения моделей [9]: «теория должна состоять из простейших моделей систем нарастающей сложности. Каждая из них должна хотя бы в минимальной степени отражать каждый из нарастающих уровней сложности поведения систем». Это означает, что главной характеристикой модели определенного уровня является отражение сложности именно данного уровня. Нельзя переносить на более высокий уровень сложности предыдущих уровней. Поэтому при решении задачи МОПТ должны использоваться обобщенные характеристики решения оптимизационных задач для подсистем связи. Такими обобщенными характеристиками являются зависимости «ресурсы-эффективность» (РЭФ) Qol (l = 1,…L , где L – число подсистем связи), каждая точка которых представляет собой решение соответствующей оптимизационной задачи, т.е. максимально возможное значение эффективности Q0l.
В [4] предлагается классифицировать рассматриваемые подсистемы тремя бинарными признаками:
1) прогрессирующие или стагнирующие;
2) независимые или зависимые;
3) массового или уникального назначения.
Разделение подсистем на прогрессирующие и стагнирующие системы связано с различием для них зависимостей РЭФ, являющихся соответственно вогнутыми и невогнутыми функциями, см. рисунок 2. С точки зрения методов решения оптимизационных задач это различие является кардинальным: для вогнутых функций, как правило, достаточным является использование следствий из теоремы Куна – Таккера [1], для невогнутых требуется применение методов типа динамического программирования, отличающихся гораздо большей сложностью.
Не менее существенно выделение зависимых и независимых систем. У независимых систем эффективность зависит только от объема ресурса, выделенного на ее развитие:
Q0l = Q0l($0l) (1)

Рис. 2. Зависимости РЭФ для прогрессирующих (а) и стагнирующих (б) систем
Решение для зависимых прогрессирующих систем может быть получено методом возможных направлений [1]. Основная трудность, однако, заключается здесь не в отыскании подходящего метода решения оптимизационной задачи, а в построении функций РЭФ, что требует одновременного анализа эффективности различных подсистем связи. Что касается зависимых стагнирующих систем, то вопрос о методах решения задач МОПТ для них остается пока открытым.
Различие между системами массового и уникального назначения состоит в том, что для систем уникального назначения недостаточно, как для систем массового назначения, в среднем хорошо выполнять задачу, когда невыполнение заданий (требований, нормативов) одними компонентами системы может быть компенсировано перевыполнением заданий другими компонентами:
Q0 = ![]() Ql.Q0l (3)
Ql.Q0l (3)
Для систем уникального назначения необходимо выполнение заданий всеми компонентами. Невыполнение задания хотя бы одним компонентом делает бесполезными любые успехи других компонентов:
Q0 = ![]() Ql.Q0l (4)
Ql.Q0l (4)
В [4] показано, что для подсистем связи массового назначения без резерва и с резервируемыми компонентами, подсистем связи с ожиданием и отказами зависимости РЭФ хорошо аппроксимируются двухпараметрическими показательными или гиперболическими функциями. Для подсистем связи уникального назначения, а также подсистем всех других типов при нелинейных функциях стоимости, такая аппроксимация оказывается неэффективной из-за невогнутости (S-образного характера) исходных зависимостей. В этом случае может использоваться табличное задание функции РЭФ, как это и предусмотрено дискретной процедурой метода динамического программирования.
Существенной в зависимости РЭФ является точка ($0l.max,Q0l.tr). Она определяет такое значение ресурса $0l.max,, при котором эффективность достигает заданного значения Q0l.tr.
Набор значений {Q0l.tr}, l=1,…, L фиксирует требования заказчика, в интересах которого создается система связи. Задача МОПТ состоит в отыскании оптимального распределения {$0l.max} заданного объема ресурса $0 между подсистемами связи, т.е. в сбалансировании потребностей ({Q0l.tr}), и возможностей ($0). Именно поэтому задачу МОПТ называют иногда задачей сбалансирования [5].
При решении мультиоптимизационной задачи возможны следующие типовые ситуации:
1. Объем выделенных ресурсов достаточен для обеспечения заданных уровней эффективности всех подсистем, т.е.
$0³![]() $0l.max = $0.max. (5)
$0l.max = $0.max. (5)
Решение задачи в этом случае тривиально:
$0l = $0l.max , l=1,…,L. (6)
2. Объем выделенных ресурсов недостаточен для обеспечения заданных уровней эффективности всех подсистем ($0<$0.max). Это означает, что при любом варианте распределения {$0l}, удовлетворяющем естественному ограничению
![]() $0l = $0. (7)
$0l = $0. (7)
у некоторых или у всех подсистем уровни эффективности будут меньше заданных значений Q0l.tr. Другими словами, каждый из векторов {$ 0l} порождает в данном случае вектор отклонений Q = (Ql,…, QL }:
Ql = Q 0l.tr – Q 0l.( $ 0l ) ³0 (8)
и скаляр
Q = maxQl, l=1,…,L. (9)
Ввиду различий, решаемых подсистемами задач, отклонения DQl с точки зрения системы в целом неравнозначны. Поэтому в качестве критерия, интегрально характеризующего вариант распределения, следует выбирать не DQ, a, например:
DQmax = max (al .DQl), l=1,..,L. (10)
где al - коэффициент важности l-ой подсистемы.
Иногда удобно в качестве критерия выбрать показатель Qsum, характеризующий суммарную эффективность всей системы. Различие в критериях порождает различные оптимизационные задачи. Математические модели МОПТ для прогрессирующих независимых подсистем одного класса при выборе одного из двух типовых критериев представлена в алгоритме решения задач по критерию DQmaxи приведена в работе [5], а по критерию Qsum – в работе [1].
Из анализа результатов в [1] делаются следующие выводы.
Значения суммарной эффективности Q1sum и Q2sum при решении по обоим критериям почти не отличаются. В то же время отличие по значениям максимального уклонения DQ1max и DQ2max настолько существенно, что не учитывать его нельзя. В связи с этим следует признать, что оптимизация по критерию DQmax является предпочтительной, поскольку она дает решения, практически оптимальные и по критерию Qsum. Обратное положение неверно. Решение, оптимальное по критерию Qsum, совершенно неудовлетворительно с точки зрения критерия DQmax.
В настоящее время является незавершенной и актуальной разработка моделей и конкретных алгоритмов МОПТ для прогрессирующих и стагнирующих независимых систем различных классов, а также для зависимых прогрессирующих систем одного класса.
В общем случае задача оптимизации указанного распределения ресурсов является принципиально многокритериальной, поскольку данное распределение приводит к результатам передачи информации, оцениваемым различными абонентами, как правило, по различным показателям качества различных услуг. Однако в отличие от многих других известных многокритериальных задач [2, 3, 6] в данном случае многие частные показатели являются однородными, что снимает проблему их нормировки. Опираясь на физический смысл частных показателей качества, подобных рассмотренным выше при пояснении первой функциональной зависимости, в [6] предложено ограничиться следующими двумя вариантами их свертки, близкими по смыслу к двум ОПК МОПТ.
В качестве первого варианта ОПК может служить аддитивная свертка (подобная второму варианту ОПК МОПТ) путем усреднения частных показателей качества {q1,...,qL}. В роли такого ОПК могут выступать средние по сети показатели качества передачи информации при предоставлении различных услуг различным абонентам сети.
Недостатком указанного варианта ОПК является его нечувствительность к различиям вида и важности передаваемой информации при предоставлении различных услуг различным абонентам. Известный способ устранения данного недостатка путем введения весовых коэффициентов при сложении частных показателей [7, 8] приводит к дополнительной проблеме обоснования значений данных коэффициентов, а также к менее ясной интерпретации физического смысла результатов свертки.
В качестве второго варианта ОПК может служить свертка частных показателей {q1,...,qL} (подобная первому варианту ОПК МОПТ) по принципу «последовательных уступок» [6]. Данный вариант свертки основан на ранжировании и последовательной нумерации всех конфигураций совместных значений показателей качества передачи информации при предоставлении различных услуг различным абонентам сети в порядке невозрастания предпочтений системы специальной связи (как единого потребителя услуг ИКС). Используемый способ нумерации данных конфигураций отражает специфику задания обобщенных требований к сетям связи, указывающих на предпочтения при неполном выполнении частных требований по передаче разноприоритетной информации.
В качестве исходных данных для расчета второго варианта ОПКQ используется вектор Q={Q1,...,QNr} показателей степени выполнения требований к качеству различных услуг для различных абонентов с различными приоритетами. Нумерация элементов вектора соответствует нумерации приоритетов r=1,...,Nr в порядке убывания их важности (т.е. больший номер соответствует меньшему приоритету). В роли показателей степени выполнения требований могут рассматриваться относительные доли сообщений, сеансов связи, направлений связи, абонентов и др. одного приоритета, качество обслуживания которых обеспечивается не ниже требуемого. Свертка указанного выше вектора Q в одно число Q осуществляется по правилу:
Q = q + Qq+1, (11)
где q имеет смысл количества приоритетов, отсчитываемых по возрастанию от более старших к более младшим до первого номера q+1, для которого ![]() <1. Если для всех r=1,...,Nr выполняется Qr=1, то Q=q=Nr . Другими словами, данный ОПК имеет вид дробно-рационального числа, целая часть которого характеризует количество приоритетов, для которых требования выполнены, а дробная часть показывает степень выполнения требований к качеству предоставления услуг следующего по важности приоритета. Описанный способ вычисления ОПК (в отличие от первого варианта ОПК) не позволяет покрыть недовыполнение требований к качеству предоставления услуг первого приоритета перевыполнением требований к качеству предоставления услуг менее важных приоритетов. При этом оказываются видны перекосы в распределении ресурсов, а также пути к их более рациональному перераспределению.
<1. Если для всех r=1,...,Nr выполняется Qr=1, то Q=q=Nr . Другими словами, данный ОПК имеет вид дробно-рационального числа, целая часть которого характеризует количество приоритетов, для которых требования выполнены, а дробная часть показывает степень выполнения требований к качеству предоставления услуг следующего по важности приоритета. Описанный способ вычисления ОПК (в отличие от первого варианта ОПК) не позволяет покрыть недовыполнение требований к качеству предоставления услуг первого приоритета перевыполнением требований к качеству предоставления услуг менее важных приоритетов. При этом оказываются видны перекосы в распределении ресурсов, а также пути к их более рациональному перераспределению.
Недостатком второго варианта ОПК является плохая “аналитичность”, затрудняющая его непосредственное использование в качестве целевой функции оптимизационных задач. Однако он является удобной мерой ограничений при решении обратных оптимизационных задач оценки степени устойчивости ИКС к внешним дестабилизирующим факторам или оценки необходимых затрат ресурсов [6].
Рецензенты:
Мякотин А.В., д.т.н., профессор, профессор кафедры Федерального государственного казенного военного образовательного учреждения высшего профессионального образования «Военная академия связи имени Маршала Советского Союза С.М. Буденного», г. Санкт-Петербург;
Одоевский С.М., д.т.н., профессор, профессор кафедры Федерального государственного казенного военного образовательного учреждения высшего профессионального образования «Военная академия связи имени Маршала Советского Союза С.М. Буденного», г. Санкт-Петербург.



