При проектировании строительных конструкций во многих случаях их расчётные схемы представляются в виде пластинок сложной формы (треугольные, ромбические, параллелограммные, трапецеидальные) с различными граничными условиями. Они применяются в качестве несущих элементов перекрытий зданий, мостовых конструкций. В настоящее время в строительной механике по-прежнему большое значение придается разработке, развитию и совершенствованию методов расчета строительных конструкций, которые позволяют путем сравнительно несложных инженерных расчётов получать оценки интегральных физических параметров конструкций.
Одним из таких методов расчета конструкций в виде упругих пластинок является метод интерполяции по коэффициенту формы (МИКФ). В основу данного метода положены изопериметрические свойства и закономерности изменения коэффициента формы области Kf при различных геометрических преобразованиях.
Коэффициент формы плоской области и является количественной характеристикой формы области и выражается через контурный интеграл [6]:
![]() , (1)
, (1)
где ds – линейный элемент контура области; h – высота, опущенная из полюса, взятого внутри области, на касательную к переменной точке контура; L – периметр области.
Коэффициент формы Kf определяется:
для параллелограммных пластинок
![]() , (2)
, (2)
где a, b – стороны параллелограмма; α – угол при основании;
для прямоугольных пластинок
![]() , (3)
, (3)
где a, b – стороны прямоугольника; k = a/b;
для ромбических пластинок:
![]() , (4)
, (4)
где α – угол при основании.
Сущность метода интерполяции по коэффициенту формы заключается в следующем. Выбирается геометрическое преобразование заданной пластинки с таким расчетом, чтобы в полученное множество форм пластинок входили хотя бы две, для которых известны решения, либо их можно получить каким-либо точным или приближенным методом. Имея опорные решения, приводим их к изопериметрическому виду [1; 2]:
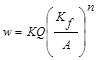 , (5)
, (5)
где n и K – неизвестные параметры.
Эти параметры определяются из известных решений (w0)1 и (w0)2, которые называются опорными решениями, а соответствующие им формы пластинок – опорными фигурами. Используем опорные решения и структуру формул, полученных при преобразовании интегро-дифференциальных соотношений технической теории пластинок:
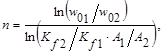 (6)
(6)
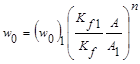 , (7)
, (7)
где индексы 1 и 2 относятся к параметрам двух опорных пластинок.
Графически рассмотренная аппроксимация изображена на рисунке 2, где кривая I соответствует действительным значениям wo, а кривая II - приближенным решениям, полученным по формуле (7). Приведенные выше рассуждения основывались на непрерывных геометрических преобразованиях, когда изменение формы фигур рассматриваемого множества происходит непрерывно и монотонно.
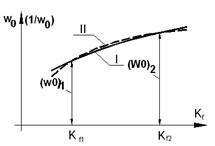
Рис. 1. График зависимости максимального прогиба от коэффициента формы.
Заданный ромб или параллелограмм может быть получен с помощью аффинных преобразований прямоугольников, а именно в результате аффинного сдвига; растяжения (при этом α = const); аффинное преобразование, при котором a/с = const. Поэтому можно получить бесконечно большое число опорных решений для нахождения прогиба ромбической или параллелограммной пластинки. Рассмотрим ромбические пластинки, нагруженные равномерно распределенной нагрузкой, имеющие комбинированное опирание.
Пример 1. Рассмотрим пластинку постоянной толщины, комбинированно опертую (рис. 2), нагруженную равномерно распределенной по всей поверхности нагрузкой. Требуется найти решение и оценить погрешность для прогиба пластинок в виде ромба с α = 35; 45; 55; 65; 75; 85.
Рис. 2. Условия опирания пластинки.
Принимаем в качестве опорных фигур пластинки в виде ромбов с α = 25 (Кf = 18,93; 1000W0 = 1,0176) и α = 90 (Кf = 8; 1000W0 = 2,208), по формулам МИКФ находим максимальный прогиб для заданных пластин; найденные данные сведены в таблицу 1.
Таблица 1
Значения максимального прогиба ромбических пластинок с комбинированными граничными условиями ![]()
|
Характеристики пластинок |
α |
|||||||
|
25 |
35 |
45 |
55 |
65 |
75 |
85 |
90 |
|
|
1000 W0 (МКЭ) |
1,0176 |
1,415 |
1,992 |
2,324 |
2,574 |
2,828 |
2,837 |
2,886 |
|
1000 W0 (МИКФ) |
|
1,427 |
1,9998 |
2,364 |
2,529 |
2,735 |
2,866 |
|
|
Кf |
18,93 |
13,947 |
11,314 |
9,766 |
8,827 |
8,282 |
8,03 |
8 |
|
Разница, % |
|
0,85 |
0,39 |
1,73 |
1,79 |
3,41 |
1,02 |
|
Пример 2. Рассмотрим пластинку постоянной толщины, комбинированно опертую (рис. 3), нагруженную равномерно распределенной по всей поверхности нагрузкой. Требуется найти решение и оценить погрешность для прогиба пластинок в виде ромба с α = 35; 45; 55; 65; 75; 85.
Принимаем в качестве опорных фигур пластинки в виде ромбов с α = 25 (Кf = 18,93; 1000W0 = 0,664) и α = 90 (Кf = 8; 1000W0 = 2,208), по формулам МИКФ находим максимальный прогиб для заданных пластин; найденные данные сведены в таблицу 2.
Рис. 3. Условия опирания пластинки.
Таблица 2
Значения максимального прогиба ромбических пластинок с комбинированными граничными условиями ![]()
|
Характеристики пластинок |
α |
|||||||
|
25 |
35 |
45 |
55 |
65 |
75 |
85 |
90 |
|
|
1000 W0 (МКЭ) |
0,664 |
1,09 |
1,459 |
1,747 |
1,92 |
2,122 |
2,186 |
2,208 |
|
1000 W0 (МИКФ) |
|
1,0926 |
1,468 |
1,764 |
1,979 |
2,1154 |
2,196 |
|
|
Кf |
18,93 |
13,947 |
11,314 |
9,766 |
8,827 |
8,282 |
8,03 |
8 |
|
Разница, % |
|
0,59 |
0,65 |
0,15 |
3,06 |
0,31 |
0,45 |
|
Анализируя результаты, представленные в таблицах 1 и 2, можно сделать вывод о том, что погрешность решения, полученного с помощью метода интерполяции по коэффициенту формы (строка 2 табл. 1 и 2) и метода конечных элементов (строка 1 табл. 1 и 2), мала и не превышает 5%.
Таким образом, МИКФ дает возможность достаточно просто и с высокой степенью точности находить значения изгиба в задачах строительной механики пластинок, связанных с ромбическими областями с комбинированными граничными условиями.
Рецензенты:
Дрозд Г.Я., д.т.н., профессор, ФГБОУ ВПО «Орловский государственный аграрный университет», г. Орел;
Шафорова О.А., д.э.н., профессор, ФГБОУ ВПО «Орловский государственный университет экономики и торговли», г. Орел.



